Simulated Rain

The latest version of our Circulating Cells program implements the simplified evaporation cycle we presented in our previous post. Freezing clouds turn into snowflakes and drift downwards. When the snowflakes pass through warm air, they melt and become raindrops. To run the program, download CC10 and follow the instructions at the top of the code.

We run the simulation starting with our cold-start state, CS_0hr. The program runs ten times slower than before. The water balancing calculations are more complex now that we have added precipitation, and we must perform them more often because rain and snow move quickly through the atmosphere. Nevertheless, a few hours running gives us six weeks of simulation time, and the atmosphere converges to the equilibrium state shown below, which you will find stored in SR_1200hr. The light gray cells are clouds of water droplets. The white cells are clouds of snowflakes. The dark gray cells are rain.



We see clouds of water droplets in the top row of cells. Here they are cooling by radiation. Our atmosphere is still opaque to long-wave radiation (transparency fraction is zero). Only the top cells can radiate into space. Their temperature is, however, well below 268 K (Tf_droplets), the temperature at which droplets are transformed into ice crystals. Snow forms within the clouds at 0.001 g/kg/s (freeze_rate_gps) and falls at 1 m/s (snow_speed_mps). When it sinks through a cell warmer than 278 K (Tm_ice), it melts at 0.01 g/kg/s (melt_rate_gps), forming rain. Rain falls at 5 m/s (rain_speed_mps).

The following graph shows how surface air temperature and average cloud depth vary with time from our cold start. The final cloud depth fluctuates by ±0.5 mm around an average value of 1.7 mm. The average temperature of the surface gas is 292 K, which is 19°C. Of the light that arrives from the Sun, 30% is reflected into space, giving our simulated planet an albedo of 0.3, which matches that of our own planet Earth.



With fast-sinking clouds, the cloud depth remained close to 2.9 mm and the surface temperature was −7°C. Evaporation from water at 19°C is roughly ten times faster than from from water at −7°C, but precipitation is so effective at removing water from the atmosphere, the sky is almost entirely clear. Indeed, the Sun shines directly upon our island half the time, heating its sandy surface up to 34°C.

Evaporation Cycle

The following diagram presents the simplified cycle of evaporation and precipitation we propose to implement in Circulating Cells Version 10.1.



Evaporation takes place from the sea, as before. When a body of moist air rises, it cools, and microscopic droplets form by condensation. Clouds of such droplets that happen to descend from above will warm up, and some or all of their droplets will evaporate. A cloud of droplets whose temperature drops below some threshold T_f will be transformed into snowflakes by the Bergeron Process, warming the surrounding gas with latent heat of fusion. We choose T_f several degrees below the freezing point of water, so we can assume the freezing takes place rapidly.

In our simulation, snow will fall at an average of 1 m/s, which we base upon our own observations. We will implement snow fall in the same way we implemented sinking clouds. Snow that reaches the surface will melt and thus take its latent heat of fusion from the surface block. This melting at the surface is the simplest way we can think of to conserve the latent heat of fusion of the water involved in our evaporation cycle. We assume that our surface water itself never freezes, no matter how cold it gets.

Our clouds, meanwhile, will no longer sink. Real cloud droplets are of order ten microns in diameter and sink at a few millimeters per second. The contribution of such sinking to our new cycle would be negligible.

Snow that enters a gas cell at a temperature greater than T_m will melt, cooling the surrounding gas by absorbing its latent heat of fusion. The melted snowflakes become raindrops a few millimeters in diameter, and these fall at 5 m/s. With the simulation set up as we have it now, the cells are around 400 m high, so rain will take a minute or two to fall out of one cell into the next. We will choose Tm several degrees above the melting point of water so we can assume the melting takes place rapidly.

Our simplified evaporation cycle omits many interesting evaporation-related phenomena. When rain drops are carried up into cold air, for example, they form hail, which later falls to Earth. When liquid rain falls into sufficiently dry air, it evaporates and disappears altogether, giving rise to virga. When air rises at just the right speed along a mountain slope, water droplets join together to form rain drops, as in orographic precipitation. Our simulation will contain none of these interesting phenomena. But we believe it will capture the fundamental features of the Earth's evaporation cycle, and so allow us to investigate how this cycle influences the global surface temperature.

Rain

Our simulated sky never clears. Clouds fill the atmosphere almost entirely. They are forever forming in air that rises from the sea, and forever sinking to the ground, but they never come falling out of the sky all at once in the big drops we know as rain.

The droplets in our clouds are tiny. Those in our slow-sinking clouds are only 10 μm in diameter and descend at 3 mm/s. Those in our fast-sinking clouds descend at 300 mm/s. The graph we present in Falling Droplets implies that these fast-sinking droplets are 100 μm in diameter. Rain falls to Earth at several meters per second, so the same graph tells us that rain drops are at least 500 μm in diameter. A drop 500 μm in diameter contains a hundred times as much water as a droplet of 100 μm and a hundred thousand times as much water as a droplet of 10 μm. Could it be that cloud droplets collide and coalesce in order to form rain drops? If so, how long does this take, and under what circumstances does it occur?

The Wikipedia page on rain describes convective precipitation and orographic precipitation. In both these forms of rain, a cloud moves up, and encounters rain drops descending from above. If the descending drops are 500 μm in diameter, and the air is moving up at 1 m/s, the drops will remain at the same altitude. The cloud moving up and past them carries microscopic droplets that can collide with the stationary drops, coalesce with them, and so enlarge them until they are heavy enough to fall out of the rising cloud and descend to the Earth as rain.

But further reading suggests that rain formed of coalescing droplets is rare. A far more potent source of rain drops are ice crystals. In Cloud Physics, we learn of the Bergeron Process, whereby ice crystals grow, sink, melt, and become rain drops. Large rain-drops are melted hail-stones. Small rain-drops are melted snow-flakes.

In our simulation, whenever the concentration of water vapor exceeds the saturation concentration, we assume the excess water condenses. It turns out, however, that the surface tension of liquid water makes it hard for water to condense into floating, microscopic droplets. If we provide a solid surface for the water to condense against, such as a blade of grass or a glass mirror, the water will condense when it reaches the saturation concentration, but in a body of air high above the ground, the only such surfaces would be dust particles, and these may be rare. Each one will serve as a catalyst for condensation until a droplet forms around it.

But the same is not true of ice crystals. In air saturated with water vapor and below the freezing point of water, an ice crystal can form on a grain of dust, and after that it will continue to grow. Water vapor deposits directly upon the surface of the crystal, thus changing state from gas to solid in one step, and the newly-created ice surface is an ideal foundation for further growth.

Now, suppose a cloud of microscopic water droplets rises until its temperature drops to −20°C. We might assume that the droplets will freeze. But pure water droplets resist freezing until they drop to −40°C. Ice crystals form in the midst of the cloud of super-cooled water droplets. As water vapor is deposited on the crystals, the concentration of water vapor in the air drops.

And here we encounter another curious physical phenomenon. The saturation concentration of water vapor with respect to an ice crystal turns out to be lower than the saturation concentration of water vapor with respect to super-cooled liquid water. Water vapor will deposit on the ice crystals until the concentration of water vapor drops to the saturation concentration of water vapor with respect to ice crystals. Because this concentration is below the saturation concentration with respect to super-cooled liquid water, the water droplets actually start to evaporate. The droplets evaporate, and their water is deposited onto larger and larger ice crystals.

Once the ice crystals are large enough, they start to fall, and they eventually fall into air that is warm enough to melt them. They turn into drops of water and fall to Earth as rain. It is this process that we will attempt to simulate in the next version of our Circulating Cells program.

Less Reflection

With 350 W/m² arriving from the Sun, 75% of the surface covered by water, clouds sinking at 300 mm/s, and each 3 mm of cloud reflecting 63% of sunlight, our CC9 simulation converges upon a surface air temperature of −12°C. When we increase the Sun's power to 400 W/m², the temperature rises by a mere 0.5°C. Our simulated planet is kept cold by thick clouds that reflect the Sun's light back into space. Ice crystals drift down from the sky in some places, while elsewhere water evaporates from the frozen seas.

The surface of the Earth is at an average temperature well above the freezing point of water, and the Earth's sky is frequently clear of clouds. Our simulated sky never clears, and the surface is frozen. It never rains in our simulation, nor do our simulated clouds emit or absorb radiation. Perhaps these two omissions are responsible for our permanent clouds and frozen seas. Before we attempt to rectify them, however, let us consider the effect of decreasing the reflecting power of our simulated clouds.

We increased Lc_water from 3.0 mm to 6.0 mm, so that it now takes 6.0 mm of cloud water to reflect 63% of the Sun's light. With the reflecting power divided in half, we ran our simulation for eight thousand hours from the starting point CS_0hr. You will find the final state in LR_8000hr.



Compared to before, we now have more clouds in the sky. The following graph shows how cloud depth and surface air temperature vary with time.



Compared to before, we see the atmosphere reaches equilibrium in on third the time. The new temperature is higher and the cloud cover is thicker. The following table compares the state of the atmosphere for both types of clouds.



Our seas are now at −3°C. If they contain salt, they will not freeze. The air a few meters above our sandy island will be just below freezing. Our simulated world is still much colder than the Earth, and nobody standing on the island would ever see the Sun. We are, however, gratified to find that our simulation remains stable with such a large drop in cloud reflectance.

Negative Feedback

With fast-sinking clouds, our circulating cells program reaches equilibrium in eight hundred hours of simulation time. With the 350 W/m² arriving continuously from the Sun, the surface air temperature settles to 261 K.

If we increase the power arriving from the sun, it seems reasonable to suppose that the surface temperature of our planet will rise. Indeed, before we added clouds to our simulation, we could use Stefan's Law to answer this question. The planet surface absorbed all the Sun's heat and the surface and tropopause radiated it all back into space, so if we increased Solar power by 4%, the absolute temperature of the surface and the tropopause would increase by 1%. But with clouds reflecting light from the Sun, we can no longer assume that all the Sun's heat will be absorbed, nor even that a constant fraction of it will be absorbed.

We ran our fast-sinking clouds simulation repeatedly from the same CS_0hr starting conditions, each time with a different Solar power. Each time we stopped the simulation after a thousand simulated hours, so that we could be sure it had reached equilibrium, and recorded the surface air temperature. We obtained the following graph.



Without clouds, a doubling of Solar power would cause the surface temperature to increase by roughly 20%. Here we increase Solar power from 200 W/m² to 400 W/m² and the surface temperature increases by only 1.5%. The following graph shows how the cloud depth increases with Solar power, thus decreasing the fraction of Solar power that penetrates to the surface.



The Sun's light, arriving at the surface, causes evaporation. This evaporation leads to clouds. But these same clouds reflect the Sun's light back into space. Thus one effect of Sunlight arriving at the surface is to reduce the amount of Sunlight arriving at the surface. The effect of clouds is an example of negative feedback. This negative feedback reduces the sensitivity of surface temperature to Solar power by more than a factor of ten.

Fast-Sinking Clouds

In our previous post we allowed the clouds in our simulation to sink to the surface at 3 mm/s. We implemented this sinking by allowing an average of 0.001% of each cell's water droplets to drop down out of the cell every second (0.1% every 100 s). Today we repeat our experiment from the same starting point, but this time the gas cells lose 0.1% of their water droplets per second, which corresponds to droplets sinking at 300 mm/s. Here is the state of the atmosphere after thirteen thousand hours.



Although our screen shot is taken at thirteen thousand hours, the atmosphere converges to its equilibrium state in a mere eight hundred hours. Our previous simulation converged only after eight thousand hours. The following graph shows surface gas temperature and cloud depth versus time.



The following table compares the equilibrium state of the atmosphere at the end of our two experiments.



The faster-sinking clouds cause the surface to warm by 5.3 K. The Solar power penetrating to the surface increases by 13 W/m² because the clouds are slightly thinner. You may recall that our current simulation of clouds does not implement their absorption and emission of long-wave radiation, so we are working with transparency fraction set to 0.0, indicating an atmospheric gas that is opaque to long-wave radiation. The only place for this artificial atmosphere to radiate is at the tropopause. So we expect to see the tropopause radiating the same amount of heat that penetrates to the surface: the heat leaving the system must be equal to the heat entering. And indeed this is the case to within a couple of Watts per square meter.

We see that faster-sinking clouds cause the world to warm up, and this is in keeping with our expectation. The icy surface must warm up so that evaporation will keep up with the greater rate of return of water to the surface.

UPDATE: It turns out that our code was allowing clouds to sink only when they took part in a circulation, which resulted in them sinking roughly a hundred times slower than they should have, so our effective sinking rate here was more like 3 mm/s. When we correct our error, so that the clouds really do sink at 300 mm/s, the surface temperature warms by roughly 7 K. [07-JAN-12]

Slow-Sinking Clouds

In Falling Droplets, we concluded that 10-μm water droplets will sink at 3 mm/s in air at pressure 100 kPa. The lowest atmospheric cells in our Circulating Cells program are at 100 kPa, and they are roughly 300 m high, so we see that it will take a hundred thousand seconds for a droplet to fall the height of the cell. Cells higher up are taller, but the gas within them is thinner. A droplet must fall more quickly through thinner air before its weight is matched by air resistance. For simplicity, we will assume that the time it takes a 10-μm droplet to fall the height of a cell is the same regardless of altitude.

As we found in Simulation Time, our program checks each gas cell every one hundred iterations on average, which corresponds to every 100 s. If it takes a droplet one hundred thousand seconds to fall the height of a cell, and the droplets in the cell are evenly distributed, 0.1% of the droplets will sink out of the cell every 100 s. If the cell rests upon a surface block, these droplets will return to the surface. We now have a way for water to leave the surface, by evaporation, and a way for water to return to the surface, by sinking. If the gas cell rests upon another gas cell, the droplets enter the cell below, where they may evaporate.

In Circulating Cells Version 9.1, we specify the sinking speed of droplets at 100 kPa with sinking_speed_mps in units of meter per second. We set sinking_speed_mps to 0.003 m/s and loaded CS_0hr into our array, which is the starting condition we used in Cold Start.

The planet warms quickly in the steady light of the Sun. After two hundred hours, the atmosphere is full of clouds and the planet starts to cool. The clouds sink towards the surface. After four thousand hours, they are thin enough that the sun starts to warm the surface. After eight thousand hours, this warming is stopped by the formation of new clouds. After a thirty thousand hours, the atmosphere settles to the steady state shown below, which you will find saved as a text array here.



The graph below plots temperature and cloud depth versus time for the first thirty thousand hours.



After thirty thousand hours, the sand and water surfaces are both at 260 K (−13°C), and the lower gas cells are at 255 K (−18°C). The average cloud depth is 3.2 mm and the average power reaching the surface is 120 W/m².

The combination of evaporation and sinking gives rise to an equilibrium in which the clouds allow just enough heat to reach the surface so that evaporation balances the return of water to the sea in the form of sinking droplets. This balance between evaporation and sinking controls the temperature of the planet surface. In our next post, we will increase the sinking speed by a factor of a hundred and see how this affects the surface temperature. We expect the surface temperature to go up, because only then will evaporation keep up with the increased loss by sinking.

UPDATE: It turns out that our code was allowing clouds to sink only when they took part in a circulation, which resulted in them sinking roughly a hundred times slower than they should have, so our effective sinking rate in this simulation was more like 0.03 mm/s. When we correct our error, so that the clouds really do sink at 3 mm/s, the surface temperature warms by roughly 7 K. [07-JAN-12]

Falling Droplets

In Clouds Without Rain we saw immortal clouds circulating above a frozen planet, reflecting the Sun's heat back into space. We concluded that it is rain that saves our planet from freezing. It is rain that clears the skies so that the Sun's heat can reach us.

We must implement rain in our simulation, so that water vapor has some way of returning to the surface. Let us begin by considering how fast water drops fall through air. A falling drop accelerates until air resistance matches its weight. At that point, it continues to fall but it does not accelerate. It has reached its terminal velocity. In The Terminal Velocity of Fall for Water Droplets in Stagnant Air, Gunn et al. describe their apparatus for measuring the terminal velocity of water droplets, and present their measurements in graphs and tables. (The paper, published in 1948, is an enjoyable read that you can download here.)

We can calculate the terminal velocity of rigid, spherical objects using Stokes Law. Gunn et al. show that Stokes' Law applies well to water droplets of diameter less than 100 μm (one tenth of a millimeter). You may recall that the droplets in our simulated clouds are roughly 10 μm in diameter (one hundredth of a millimeter). For the droplets are small enough, surface tension is able to maintain a spherical shape in the face of air resistance.

But for droplets larger than 100 μm, Stokes Law over-estimates the terminal velocity. Larger droplets assume flattened shapes as they fall, and they are in constant motion, so that the air resistance they encounter is far greater than it would be for a rigid sphere. When the diameter exceeds 5 mm, the motion of the drop becomes so vigorous that the drop breaks into smaller drops.

The following graph shows the Gunn et al. measurements of terminal velocity, plotted against droplet diameter. We see that the maximum terminal velocity for the largest possible water droplets is around 10 m/s. For diameters less than 0.1 mm, Gunn et al. assure us we can use the terminal velocity given by Stoke's Law, so we also plot the terminal velocity calculated from Stokes' Law.



The 10-μm droplets in our simulated clouds will fall at a mere 3 mm/s through our gas cells. Given that our cells are a few hundred meters high, it will take a day or two for a cloud to fall from one cell to the cell below. Slow as this may be, the sinking of clouds does provide a way for water to move from one cell to another, and ultimately to return to the planet surface. In our next post, we will see how sinking clouds affect the result of our Cold Start simulation.

Cold Start

In our previous post, we presented our simulation of clouds without rain. We started the atmospheric gas, the sandy island, and the watery sea, at a uniform 280 K (7°C). Water evaporated from the sea. The sand heated up in the sun. Hot air rose above the island and sucked moist air in from the sea. Clouds formed above the island, spread through the atmosphere, reflected the heat of the sun, and the world froze.

What if we start with a frozen world and a dry atmosphere? In our simulation of evaporation rate, no water will evaporate from a sea at 250 K (−23°C), so no clouds will form. We ran CC9, starting with the CS_0hr array, to find out what would happen. Our starting point is a uniform 250 K with no water vapor. We run with 350 W/m² continuous heat from the Sun.

After 20 hrs, the sandy island has warmed to 276 K (3°C). At 30 hrs, the average cloud depth is 0.03 mm, which is so thin that we don't bother plotting the clouds as white cells. But at 40 hrs we start to see the first thin clouds, and the average power arriving from the Sun drops to 335 W/m². At 50 hrs, the island reaches 283 K (10°C). From here on, it cools. At 100 hrs, the average cloud depth is 3.5 mm and only 120 W/m² is arriving from the Sun. The sea reaches 267 K (−6°C), which is the warmest it will ever get. By 200 hrs, cloud depth is 7.2 mm and power arriving from the Sun is only 40 W/m², as recored in CS_200hr.

We can see where the simulation is going to end up: a world kept frozen by immortal clouds. Regardless of our starting point, immortal clouds reflect the Sun's heat and cause the world to freeze.

Clouds Without Rain

Today we present Circulating Cells Version 9 (CC9), and we use it to find out what would happen if we had clouds without rain. The simulation implements the following features of clouds.

(1) Evaporation from surface water, as in Evaporation Rate.
(2) Condensation in rising air, as in Condensation Point and Condensation Rate.
(3) Cooling and warming by latent heat of evaporation, as in Latent Heat.
(4) Reflection of incoming sunlight, as in Simulated Clouds, Part I.

The simulation does not yet implement the following features of clouds.

(5) Absorption and emission of long-wave radiation, as in Simulated Clouds, Part II.
(6) Cooling and warming by latent heat of fusion, as in Latent Heat.
(7) Rain and snow.

If we set the simulated atmosphere's transparency fraction to 0.0, we make the atmospheric gas opaque to long-wave radiation. No radiation escapes into space from the surface blocks nor from the rows of gas cells below the top row, regardless of the distribution of clouds within the atmosphere. The top row of cells, which is our simulated tropopause, does all the radiating of heat into space. Although this opaque atmosphere is not realistic, it does mask the fact that our clouds do not in themselves absorb or emit long-wave radiation, allowing us to proceed with a simulation that is at least self-consistent. Thus the copy of CC9 that you can download today has the transparency fraction set to 0.0 by default.

We ignore the warming of rising air by freezing water droplets, and the cooling of falling air by melting ice crystals. We will add ice crystals to our simulation later. For now, we trust that the error caused by our omission is not so great as to overturn the observations we make today.

By ignoring rain and snow, we are ignoring a feature of clouds that is so important to our climate that our simulation produces an entirely fantastic result. To watch the simulation in action, download CC9 and follow the instructions at the top of the code to run the program on your computer. Get the CWR_0hr array file and load it with the Load button. You will see an atmosphere at a uniform 280 K, and down at the bottom, an island of sand in a sea of water, also at 280 K. Press Run and the simulation will begin. The CC9 code runs in "Day" mode by default, with 350 W/m² arriving continuously from the sun.

Without rain and snow, any and all moisture that enters the atmosphere at the beginning of the simulation remains in the atmosphere for as long as the simulation runs. There is no means by which moisture can return to the surface of the planet. So long as the lower atmosphere is warm enough to absorb water vapor, however, the clouds can appear and disappear. The moisture they contain can either take the form of water vapor, as it will when the surrounding gas is warm, or it can take the form of water droplets, as it will when the surrounding gas is cold.

We represent clouds in our simulation with cells that are shaded white to gray. The thinnest clouds are white and the thickest are black. A cloud with 1 mm of water is white. A cloud with 12 mm of water is black. After 30 hours, the first white clouds appear over the island, the result of moist air from the sea being heated by the island and rising towards the tropopause. When it rises, it cools, and water vapor condenses to form the first clouds.

At 40 hours, the island reaches its peak temperature of around 311 K. After that, the clouds become more numerous. They reflect the Sun's light back into space. The surface begins to cool. After 150 hrs we end up with the following display.



There is fog over the sea and part of the island. There are thick clouds up in the tropopause. The average heat arriving at the surface from the Sun has dropped from 350 W/m² to only 50 W/m². The following graph shows how the atmosphere cools in the first 500 hrs.



Let us refer to the combined thickness of the clouds above a surface block as is its cloud cover. In our simulation, each 3 mm of cloud cover reflects 63% of incoming sunlight. If we press the Data button, a text window opens and here we will see a line of numbers printed every hour of simulation time. The first number is the time in hours, the second is the average cloud cover in millimeters. The third number is the average sunlight power penetrating to the surface through the cloud cover in Watt per square meter. After that we have four temperatures in Kelvin: average sand temperature, average water temperature, average surface gas temperature, and average tropopause temperature. We used these printed lines to obtain the data for the plot above.

After 3000 hrs, the tropopause has dropped to 158 K (−115°C) and the surface air is at 184 K (−85°C). The average cloud cover is 25 mm. Only 0.7 W/m² arrives at the surface. You can see this for yourself by loading CWR_3000hr into the simulation. Even at 158 K, the tropopause is still radiating 35 W/m², which is far more than the 0.7 W/m² reaching the planet surface. The tropopause will keep cooling until it reaches 60 K, at which point it will be radiating 0.7 W/m². Of course, at that point, nitrogen will condense into liquid.

If clouds remained aloft in the atmosphere indefinitely, the Earth would freeze. But in reality, clouds are forever falling towards the ground. They are made of droplets and crystals that are heavier than air. Rain and snow are what stop clouds from turning the Earth into a planet of frozen seas.

Summary to Date

Once we were satisfied that our simulation handled convection properly, that we could relate the program iterations to the passage of time, and that all the heat entering the simulated system was accounted for by radiation from the top, we added blocks of either water or sand beneath the bottom gas cells, so as to simulate the planet surface. In Back Radiation we showed how the heat capacity and radiation produced by a semi-transparent atmosphere keeps the planet surface warm at night. In Island Inversion we see the surface of an island heating up ten times more than the surrounding ocean, while at night a layer of air a few hundred meters above the island is warmer, rather than cooler, than the air resting upon the island. Thus we see our simulation is consistent with our observations of surface cooling, including even temperature inversion.

Well-satisfied with our simulation of a dry atmosphere, we now turn to the simulation of a wet atmosphere, in which evaporation will cool the ocean and lead to the formation of clouds. To simulate cloud formation, we must have equations for the rate of evaporation from a water surface, the rate at which water vapor will condense out of rising air, the rate at which it will evaporate again in falling air, the cooling effect of evaporation upon the water surface, the warming effect of condensation upon the rising air, the amount of sunlight that will be reflected by existing clouds, and the amount of long-wave radiation that these same clouds will absorb and radiate. We obtained these relations in a series of posts Evaporation Rate to Consensation Rate. We have yet to consider the downward drift of water droplets that leads to their combining together and forming rain. But after so many posts of mathematics and empirical relations, we thought it was time to get back to the simulation, and so we will start our simulation of clouds without allowing rain, and perhaps we will see how important rain is for our climate.

We are running CC9 right now, and will present it later this week, once I have made a reasonable effort to eliminate errors from my implementation of evaporation, condensation, and reflection. The clouds are going round right now, as gray-shaded cells, and the effect is entertaining. Ultimately, you may recall, our objective is to see how a change in the transparency of the dry atmosphere affects the surface temperature of the planet, so that we can determine the effect of CO2 doubling within a system dominated by the effect of cloud formation and rain.

Condensation Rate

in Condensation Point we considered the temperature at which water vapor will begin to condense into water droplets, thus making a cloud. We did not consider how fast this condensation will take place. Consider air with 20 g/kg of water vapor (that's 20 g of water vapor mixed with each 1 kg of dry air to make 1.020 kg of moist air). This air rises rapidly, expands, and cools to a point where its saturation concentration of water vapor is only 10 g/kg. Does the excess 10 g/kg condense into droplets immediately, or does it take some time, in the same way that the original evaporation took time?

As we saw in Latent Heat, the evaporation of water requires 2.2 kJ of heat for each gram of evaporating water. Because we must put energy into the water to make it evaporate, evaporation takes place slowly. In the case of condensation, however, the exact opposite is the case: condensation liberates 2.2 kJ of heat for each gram of water that condenses. Condensation takes place much more quickly, but it cannot take place instantly. In order for condensation to take place, water vapor molecules must bump into one another and stick together. A dust particle helps accelerate the condensation process by providing a surface upon which water molecules can condense. Until such time as all condensation is complete, the water vapor concentration remains greater than the saturation concentration, and we say the water vapor is supersaturated.

The cloud chambers of early high energy physics experiments used supersaturated water vapor to detect charged sub-atomic particles. A cloud chamber consists of a piston with a glass top. We fill the piston with moist air and pull the piston down rapidly, so that the air cools by adiabatic expansion and becomes supersaturated. When a charged particle, such as a cosmic ray, passes through the chamber, water condenses into a trail along its path. Indeed, cosmic rays may play a part in promoting cloud formation in our atmosphere. The CLOUD experiment is an effort by high energy physicists to apply their experience with cloud chambers to the study of cosmic rays and cloud formation, especially cloud formation at high altitudes where the air is thin and the water vapor is scarce.

Even in a cloud chamber, however, supersaturated water vapor does not endure for long. A useful cloud chamber has a piston going up and down several times a second because the water vapor condenses on its own within a fraction of a second. In our Circulating Cells program, we will check the water vapor concentration of the cells every hundred seconds or so. For the purpose of our simulation, therefore, we will assume that condensation within a cell is complete within a hundred seconds. When we find a cell with 20 g/kg of water vapor and a saturation concentration of 10 g/kg, we will allow 10 g/kg to condense into droplets.

Not only do we expect to encounter moist air rising and cooling, we will also have cloudy air falling and warming. As it warms, the saturation concentration increases, so it is possible for some or all of the water in the droplets to evaporate again. Because evaporation rate is proportional to the surface area of water, the tiny droplets of a cloud will evaporate quickly. The 20-μm diameter droplets of a cloud provide 3000 cm² of surface area for each gram of water they contain. A 1-cm deep puddle, meanwhile, provides only 1 cm²/g. We expect cloud droplets to evaporate three thousand times more quickly than a 1-cm deep puddle. A 1-cm deep puddle will evaporate in less than ten thousand seconds, so a cloud will evaporate in less than thirty seconds. For the purpose of our simulation, therefore, we will assume that the evaporation of cloud droplets is complete within a hundred seconds.

Combining these two assumptions together, we see that whenever our simulation encounters a gas cell with water vapor concentration greater than the saturation concentration, we will remove the excess water vapor and turn it into cloud droplets. Conversely, whenever we have cloud droplets with water vapor concentration less than the saturation concentration, we will remove however many cloud droplets we can until the water vapor concentration is again equal to the saturation concentration.

Simulated Clouds, Part II

In Part 1, we gauged the thickness of a cloud by how deep a layer of water it would make if we combined all its water droplets into a pool of the same area as the cloud. A thin cloud might contain 1 mm of water, while a thick storm cloud might contain 100 mm.

We also concluded that even the thinnest of clouds is opaque to long-wave radiation, and therefore a good radiator of its own heat. Meanwhile, clouds do not absorb short-wave radiation from the sun at all because water is transparent to sunlight. Instead, they reflect sunlight back into space. For the purpose of our Circulating Cells simulation, we decided that each 330 μm thickness of water will reflect 10% of sunlight. Perhaps that's too much reflection, perhaps it's too little. We can adjust the 10% reflection depth later if we need to.

Suppose we have a 1-mm cloud layer up near the tropopause, and a 10-mm cloud layer nearer the ground. The combined thickness of both clouds is 11 mm, from which we deduce that only 3% of sunlight will penetrate to the planet surface. This is a calculation we can perform easily in our simulation. We add the thickness of the clouds above each surface block, and apply our formula for reflection to obtain the fraction of sunlight arriving at the surface.

More complicated than the incoming sunlight is the absorption and radiation of heat by separate cloud layers. The surface radiates heat as if it were a black body, but our simulated atmospheric gas has a transparency fraction, which tells us the fraction of long-wave radiation passing through the gas. The rest of the radiation is absorbed. Suppose our transparency fraction is 60%, then 60% of the heat radiated by the surface will reach the bottom layer of cloud, where all of it is absorbed. The cloud itself radiates heat in proportion to the fourth power of its temperature, as if it were a black body, and of this heat 40% is absorbed immediately by the gas above, below, and even at the center of the cloud. The remaining 60% passes down to the surface and up to the upper layer of cloud. The upper layer of cloud absorbs all the radiation from below, and itself radiates heat in proportion to the fourth power of its temperature, as if it were a black body. Of the heat radiated by the upper cloud, 60% will pass back down to the bottom layer of cloud and out into space.

Thus we see that we have long-wave radiation flowing in both directions because of the clouds. If we had just one, thick, cloud layer, our calculation would be simpler. But we have fifteen rows of cells in our simulation, so we could have seven layers of cloud, each separated by a row of gas cells. Our way of handling this problem will be as follows.

For each column of cells, we start at the top and make our way down to the surface. When we encounter a cloud, we calculate how much heat it radiates downwards from its bottom surface. We proceed until we reach another cloud, and here we allow the downward heat to be absorbed at the top surface of the cloud. We continue to the bottom surface of the cloud, and keep going with the same procedure until we get to the surface. By this time we have added up the total cloud thickness and we can determine how much sunlight has reached the surface as well.

Now we start from the surface and go upwards. The surface radiates heat, and this is absorbed by the bottom surface of the lowest cloud. The top surface of this cloud radiates heat upwards. If there is another cloud above, its bottom surface will absorb the upward-going heat, but if there is no other cloud, the heat passes into space.

During this entire process, we keep track of the amount of heat that is added or subtracted from the surface and from each gas cell. Once we are done, we adjust their temperatures to account for the heat lost or gained.

Thus we see that our clouds will introduce new sources of radiation into space that are at a lower altitude than the tropopause that is currently doing all the radiating into space of our simulated atmosphere. On the other hand, the clouds obscure the hottest radiating surface of all, which is the ground.

Our calculation of up-welling and down-welling radiation might slow down our simulation a great deal. But we're not in any hurry, so we won't worry about the computation time.

Simulated Clouds, Part I

When water condenses within a rising body of air, it forms a cloud of liquid droplets. A thickness of more than 20 μm of liquid water is opaque to long-wave radiation. In Clouds we showed that even a sparse cloud is a near-perfect absorber of long-wave radiation. By radiative symmetry, clouds are also near-perfect emitters of long-wave radiation. At the same time, we showed that clouds do not absorb short-wave radiation, such as sunlight. They either reflect it or allow it to pass through without absorption.

We will soon implement cloud formation in our Circulating Cells program. We must decide how to implement their absorption and emission of long-wave radiation, and their reflection of sunlight.

Looking at our graph of saturation concentration, we see that air with 50% humidity at 300 K contains around 25 g/kg of water. Suppose this air rises and a mere 1 g/kg of water vapor condenses. Our gas cells have mass 330 kg/m², so when 1 g/kg of water condenses, there will be 330 g of water over each square meter of the cell's base area. This 330 g, if spread over a square meter, has depth 330 μm. According to our absorption spectrum for water, 330 μm of liquid water is more than enough to absorb all long-wave radiation, but not enough to absorb even 1% of sunlight.

The condensed water forms a cloud of water droplets. Cloud droplets are typically twenty micrometers in diameter. Our 330 g/m² will form roughly a hundred billion such droplets. Sunlight passing vertically down through the cloud will encounter roughly thirty such droplets. Each drop will reflect and refract the light. We estimate that 10% of the descending sunlight will be reflected back out into space by such a cloud, while 90% will continue onwards. When 10 g/kg of water condenses, we will have 3.3 kg/m² of water vapor, and sunlight will encounter 300 droplets instead of 30. The fraction of light passing through the cloud will be 0.9¹⁰ = 35%, while 65% is reflected.

Thus we have a way of taking the concentration of condensed water in a gas cell, and calculating the fraction of light it will reflect back into space. We also have a simple way of handling the absorption and emission of long-wave radiation by clouds: any cloud in our simulation will be a both a perfect absorber and a perfect emitter of long-wave radiation.

Latent Heat

In Evaporation Rate we considered the rate at which water evaporates from the sea, and in Condensation Point we considered the amount of water that will condense from humid air when it cools down. Today we consider the heat absorbed by evaporating water, and the heat liberated by condensing water vapor.

It takes 2.2 MJ of heat to evaporate one kilogram of water. This heat is called the latent heat of evaporation. Two million Joules is enough energy to raise a 100 kg load to the top of a two thousand meter mountain. It is the energy released by the explosion of a stick of dynamite, or the energy we obtain from eating two jelly donuts.

For the purpose of our simulation, let us suppose that only the top one meter of water supplies the heat of evaporation. The heat capacity of water is 4.2 kJ/kg, so our surface blocks of water will have heat capacity of 4.2 MJ/m². In an earlier example, we found that roughly 1.8 kg of water will evaporate every hour from each square meter of a lake at 290 K (14°C). The latent heat carried away by the evaporating water will come from the heat of the water it leaves behind, so the lake surface will cool by roughly 1°C/hr.

As we saw in Back Radiation, the lake absorbs heat from the sun during the day, and always radiates heat upwards. In Surface Cooling, Part I, we showed how a water surface heats up by less than 1°C during the day. A lake does not get hot enough with respect to the air above to cause significant convection. Thus heat loss by a water surface is dominated by radiation and evaporation.

When water vapor condenses from cooling, humid air, it releases its latent heat into the air around it. The volume occupied by the water vapor decreases by a factor of a thousand then it condenses, but at the same time its latent heat warms up the air, causing the air to expand. In Condensation and Convection we found that the expansion due to warming dominates the contraction due to condensation by almost an order of magnitude. A single gram of water vapor condensing out of kilogram of air causes the air volume to increase by 1%. When air expands, it becomes buoyant, so it will have latent heat of fusion. This is the heat required to melt ice, which is liberated when the water freezes. Water's latent heat of fusion is roughly 330 kJ/kg. If we have one gram of water freezing in 1 kg of air, the air will warm by roughly 0.3°C.

We can now implement in our Circulating Cells program the evaporation of water from the planet surface, its subsequent condensation into clouds of droplets in rising gas cells, and its eventual freezing into ice crystals. These clouds will, however, have a strong effect upon the manner in which the atmosphere radiates heat into space.

In Thick Clouds we saw how low, thick clouds block the sun's light from reaching the ground, thus causing it to cool down. In High Clouds we saw how thin, high clouds allow the sun's light to pass through, but block radiation by the planet surface, thus causing the surface to warm up.

Before we can implement clouds properly in our simulation, we must consider how to model their effect upon sunlight and radiation.

Condensation Point

Suppose a body of moist air rises from the surface of the sea. The weight of air pressing down upon it decreases as it rises. Its pressure drops. It expands and cools adiabatically (see Adiabatic Balloons). So long as no condensation occurs, its temperature drops by 1°C for each 100 m that it ascends (see Tempearture, Pressure, and Altitude). Will the water vapor eventually condense into droplets?

If we know the initial concentration of water vapor in grams of water per kilogram of air, this concentration will remain constant as the air moves upwards. As the temperature of the air drops, however, perhaps there will come a time when the concentration of water vapor exceeds the saturation concentration, and at that point droplets will form. In Evaporation Rate we presented a graph of saturation concentration versus air temperature. But the data points of this graph correspond to measurements taken on the surface of the Earth, where air pressure is 100 kPa. What will the saturation concentration be at the lower pressures that apply to our rising body of air?

The pressure exerted by a gas is the force exerted by its molecules bouncing off whatever surface they encounter. The pressure of moist air is the sum of the pressures exerted by its nitrogen, oxygen, water, and all other molecules. The pressure exerted by the nitrogen molecules is the partial pressure of nitrogen. The pressure exerted by the water molecules is the partial pressure of water. It turns out that the maximum possible partial pressure of water molecules depends only upon temperature. This maximum is the saturation pressure of water at a particular temperature. Regardless of the other gases that might be mixed with the water vapor, the saturation pressure is always the same at a particular temperature. The graph below gives saturation pressure versus temperature, as indicated by an empirical formula we found here.



Water vapor is a gas just like nitrogen and oxygen. Its pressure depends only upon its volume and temperature. Water vapor in moist air will be at the same temperature as the air. It will share the same volume as the air. If the air pressure halves, so does the partial pressure of water vapor. For concentrations below a few percent, the concentration of water vapor at various air pressures is given by:

x = p_wR_w/pR = 0.62 p_w/p,

where x is the concentration of water vapor, p_w is its partial pressure, R_w is its specific gas constant, or 462 J/kgK, p is the air pressure, and R is the specific gas constant for air, or 287 J/kgK.

Consider moist air near the surface of the Earth at temperature 300 K, pressure 100 kPa, and water vapor partial pressure 2 kPa, which corresponds to concentration 12 g/kg. The water vapor pressure is roughly half the saturation pressure of 3.8 kPa shown on our graph. Suppose our moist air rises to 2000 m. Its cools to 280 K (1 K per 100 m) and its pressure drops to 80 kPa (adiabatic expansion of air). The concentration of water vapor remains 12 g/kg and its partial pressure drops slightly to 1.6 kPa. At 280 K, however, the saturation pressure has dropped all the way to 1 kPa, which corresponds to a concentration of only 7.6 g/kg. Thus each kilogram of air contains 4.4 g more water than it can hold as water vapor. This excess water must condense to form water droplets.

We would like a simple formula that will allow us to calculate the amount of water that must condense from moist, rising air in our Circulating Cells program. We combine the saturation concentration approximation of our Evaporation Rate post with the specific gas constants of air and water vapor, and with the assumption that the water vapor concentration is small, to arrive at the following approximation.

x_s = (T−250)²p/8000

Here x_s is the saturation concentration of water vapor in g/kg, p is the air pressure in kPa, and T is the temperature of the air in K. At 280 K and 80 kPa, this formula gives us 9 g/kg, which corresponds to a partial pressure of 1.2 kPa. This 1.2 kPa is close enough to the 1.0 kPa shown in the graph above.

The partial pressure of water vapor in moist air decreases as the air rises. But at the same time, the rising air cools by adiabatic expansion, and this cooling depresses the saturation pressure of water vapor so rapidly that condensation will eventually take place. With our approximate formula for saturation concentration with pressure and temperature, we will be able to simulate the condensation of water in moist, rising air.

Evaporation Rate

We are preparing to add evaporation from surface water to our Circulating Cells program. Water will leave the surface and enter the atmosphere as water vapor. The rate at which water evaporates depends upon the humidity and movement of the air above. The following empirical equation, which we found here, tells us the approximate rate at which water will evaporate into air, assuming the air is at roughly the same temperature as the water.

w = (0.007 + 0.005v)(x_s − x),

where w is the evaporation rate in grams per second for each square meter of water surface (g/m²s), v is the velocity of the air in meter per second (m/s), x_s is the saturation concentration of water vapor in grams of water per kilogram of dry air (g/kg) for air at the same temperature as the water, and x is the actual concentration of water vapor in grams per kilogram of dry air (g/kg) in the air above the water.

In our simulation, we know the temperature of the surface water, and when we simulate a planet with a water surface using CC8, we find that the surface gas cells are within a few degrees of the temperature of the surface water. Our previous work on impetus for circulation suggests that the velocity of our gas cells is of order 4 m/s. When we implement evaporation, we will keep track of the water vapor concentration in each cell, so we will know x. What remains for us to determine is x_s, the saturation concentration of water vapor in air at the surface temperature.

The following graph shows measured values of saturation concentration in g/kg for a range of temperatures in Kelvin, based upon data we found here. To see the same plot in Centigrade, see here.



Also plotted on the graph is a parabolic approximation to the measured data, which is based upon two reference points: 0 g/kg at 250 K and 45 g/kg at 310 K. This approximation is good enough for our purposes, and will simplify our program. Thus our evaporation equation becomes:

w = [(T−250)²/80 − x] / 40

For example, if we have dry air over a lake at 290 K (14°C), water will evaporate at 0.5 g/m²s. In one hour, 1.8 kg of water will evaporate from each square meter. Our gas cells have mass 330 kg/m², so after an hour over the lake, the gas will acquire water vapor concentration 5 g/kg, which is well below the saturation concentration of 20 g/kg given by our approximation. Its relative humidity will be 25%.

Island Inversion

We invite you to download Circulating Cells, Version 8.4 by clicking here so that you can watch it simulate air movement above an island in the sea. Start the program and set it to Cycle mode with Q_sun set to 700 W/m². Download this file and read it into the simulation with the Load button. You will see the an island of sand at the center of the surface blocks, surrounded by water on the left and right. The saved state of the cell corresponds to midnight, so you can start the simulation right away.

Just before dawn, at solar time 5.5 hr, you will see that the temperature of the air resting upon the sand of the island is slightly cooler than the air above. The following figure is a close-up of the air above the sand, in which ran the program with max_T set to 300 K and min_T set to 260 K in the source code so as to make the cool layer more obvious. Note that the orange-lined surface blocks are sand and the blue-lined ones are water.



Our simulation produces the inversion of atmospheric temperature that we discussed in Surface Cooling, Part IV. In that post, we proposed that the leaves of a forest would cool at night by radiation. Air in contact with the leaves would descend to the ground and drag warmer air down from above. We suggested that this process might cool the first ten to a hundred meters of air above the treetops, producing temperature inversion. Perhaps that is indeed what happens over a forest. But in our simulation, whenever the surface is cooler than the air resting upon it, we set the heat transfer by convection and conduction to zero. How, then, does inversion occur over our simulated island?

The sandy island cools by roughly 50°C to −12°C at night. At this temperature, it radiates only 260 W/m². Of this, 130 W/m² is absorbed by the bottom layer of the atmosphere, because we have transparency fraction set to 0.5. Meanwhile, the bottom layer of our simulated atmosphere radiates heat both night and day. At the start of the night, its temperature is around 300 K and it radiates 230 W/m² to the sand below, which is half the heat a black body at that same temperature would radiate. By radiation alone, we see that the cells above the sand are losing 100 W/m².

The mass of our cells is 330 kg/m², and their heat capacity at constant pressure is 1 kJ/kg, so 100 W/m² will cool them by roughly 1°C/hr. This is what we see during the night above our island. Inversion does not occur over the water because the water surface in our simulation has ten times the heat capacity as the sand, and so cools ten times less at night. The water continues to warm the lower atmosphere with its radiation during the night. Thus we see how back-radiation and a surface with low heat capacity work together to produce temperature inversion.

Back Radiation

In our Rotating Greenhouse post, we use CC5 to simulate the alternation between day and night by varying the Solar power delivered to the gas cells resting upon our simulated planet surface. But we did not simulate the surface itself, nor did we distinguish between the temperature of the surface gas and the radiating temperature of the planet surface: we used the same temperature. But the CC8 program we introduced in our previous post does simulate the planet surface, so we can see how the temperature of the sand itself varies with day and night.

During the day, most of the heat passing into the surface gas cells does so by convection. But convection occurs only when the gas above is cooler than the surface below. In our discussion of atmospheric inversion we saw how the ground can be colder than the surface air at night, which can lead to a pocket of cold air sitting near the ground, with warmer air up above. In our simulation, we set the convection transfer to zero when the surface is colder than the surface gas.

At night, therefore, a sandy surface will radiate its heat into space, and receive no warmth from the sun. But it will receive warmth from the atmosphere, in the form of the back-radiation we described in our previous post. During the day, we found that our surface gas was radiating 226 W/m² down to the surface. This radiation will slow the cooling of the surface at night.

We ran our simulation with Cycle heating on a sandy planet surface, 700 W/m² solar heat during the day, daylight fraction set to 0.50, convection coefficient 20 W/m², and transparency fraction 0.50. You will find the equilibrium state of the cell array at midnight stored in a text file here. The following graph shows the average temperature of the sand blocks, the surface gas cells, and the tropopause gas cells during two complete day-night cycles. We plot the deviation of each temperature from its average value during the cycles, which is why we call the plots "anomalies".



The temperature of the surface sand varies by almost 50°C, dropping as low as −12°C just before dawn. The temperature of the air a hundred meters above the sand, at the center of the bottom row of gas cells, varies by 9°C, dropping as low as 23°C. The tropopause responds far less to the day-nigh cycle, with a variation of only 2°C. These results are consistent with our observations of the desert, which we discussed at length in our Surface Cooling posts.

When we turn off the back-radiation in our simulation, the temperature of the surface sand drops by another 50°C at night, in a manner reminiscent of the Moon. And so we conclude that our atmosphere, by means of back-radiation, keeps us warm at night.

Simulated Planet Surface

Our Circulating Cells Version 8.3 simulates the planet surface with a row of blocks. You can download the latest code here. These blocks can be sand or water. If they are sand, they have low heat capacity and warm up quickly in the Sun's light. If they are water, they have high heat capacity and warm up slowly. By clicking upon one of the blocks, we change it from one type to the other.

In the long run, we will implement evaporation from the water blocks, but for now we concentrate upon the heat exchange between the surface and the atmosphere. In previous versions of our program, we allowed sunlight to pass directly into the surface gas cells. Now we allow sunlight to pass all the way through the entire atmosphere to be absorbed at a solid or liquid surface. Real water reflects 4% of short-wave radiation, and sand reflects something like 10%, but our simulated water and sand absorbs all short-wave radiation.

Both sand and water are near-perfect emitters of long-wave radiation, so we allow our surface blocks to radiate heat according to Stefan's Law. We also allow heat to leave the surface blocks by convection. We determine the convection heat loss by multiplying the temperature difference between the surface and the gas by a convection coefficient. This heat leaves the surface block and enters the gas cell above.

As we described in our previous post, our simulated atmosphere is partially-transparent, to an extent specified by the transparency fraction, τ. The gas above a surface block absorbs a fraction 1−τ of the block's radiation, and the remainder passes out into space. We add the absorbed heat to the gas cell above the surface block.

Now we come to a component in the heat exchange between the atmosphere and the surface that we have not simulated or calculated before. The atmosphere itself will radiate heat downwards towards the surface, and the surface, being a perfect absorber of such radiation, will absorb all of it. The heat radiated downward by the atmosphere is often called back-radiation or downward long-wave radiation. To calculate the back-radiation, we use the same equation we applied to the tropopause in our previous post. When the transparency fraction is 0.5, the gas radiates half as much heat as a black body at the same temperature.

We ran our simulation with Day heating of 350 W/m², all surface blocks made of sand, convection coefficient 20 W/m²K, and transparency fraction 0.50. The following figure shows the equilibrium state of the array. The surface blocks are color-coded for temperature in the same way as the gas cells, but they have an orange border to mark them as sand. A water cell has a blue border. You will find the equilibrium state of the array saved as a text file here.



As in our previous simulations, the temperature drop from the surface gas cells to the tropopause gas cells is very close to 50 K. The sandy surface settles to 303.0 K, at which temperature it radiates 480 W/m². Of this, 240 W/m² passes directly into space and 240 W/m² is absorbed by the gas above. The tropopause settles to 249.0 K and radiates 110 W/m² into space. The total radiation into space is 350 W/m², which is the amount that is arriving from the sun, so our planet is in thermal equilibrium.

The 110 W/m² radiated by the tropopause must pass up through the atmosphere by convection. The surface gas is at an average temperature of 298.5 K, radiating 226 W/m² back to the surface. Thus a net 14 W/m² passes from the surface to the atmosphere by radiation. The remaining 96 W/m² passes into the atmosphere by convection at the surface. The surface is on average 4.5 K warmer than the gas, for which we expect only 90 W/m² to flow by convection. But the gas cells warm by roughly 8 K while they sit upon the sand. When they first arrive from above, they are almost 10 K cooler, and 200 W/m² flows into them by convection. Just before they rise up, they are only 2 K cooler, at which point only 40 W/m² flows into them. When we get the program to print out the convection rate, we obtain an average of 96 W/m², so all the heat from the Sun is accounted for.

We note that almost all the heat flowing from the surface to the atmosphere is carried by convection. The heat radiated by the surface and absorbed by the atmosphere is nearly balanced by the radiation returned by this same atmosphere. The difference is only 14 W/m², compared to 96 W/m² passing into the gas by convection. In our next post, we will simulate night and day over a sandy desert and see if we come up with reasonable variations in temperature at the sandy surface, the air above the surface, and the air high up in the tropopause.

Simulated CO2 Doubling

In Planetary Greenhouse we considered an atmosphere transparent to some long-wave radiation and opaque to others. In Circulating Cells Version 8.2, which you can download here, we simulate such an atmosphere with the new transparency fraction parameter.

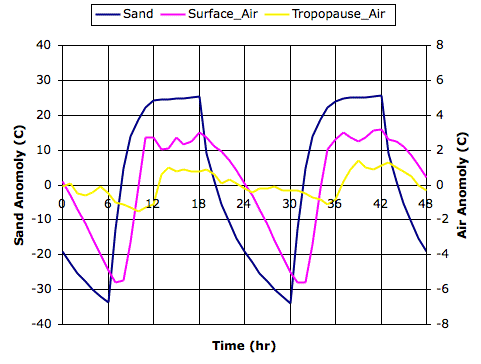
For the moment, we ignore the temperature difference that must exist between the planet surface and the lower atmosphere (see Surface Cooling, Part VI). We assume that the solid or liquid surface beneath one of the bottom gas cells will be at the same temperature as the gas itself. Ever since our Earth Radiator post, we have assumed that the surface of a planet is a black body radiator. If a bottom cell is at 300 K, the surface below will be at 300 K also, and by Stefan's Law it will radiate 460 W/m². At 303 K, the radiated power increases to 480 W/m². Black-body radiation increases as the fourth power of the temperature, so a 1% increase in temperature causes a 4% increase in radiated power.

The absorption spectrum of the Earth's atmospheric layers varies in a complex and dramatic way with wavelength, as you can see here. What made our Total Escaping Power calculation so complicated was that we had to deal with the partial absorption of some wavelengths by each atmospheric layer, and therefore the partial emission of these same wavelengths by the same atmospheric layers. We want to avoid the complexity of partial absorption at a given wavelength, so we assume that the gas in our CC8 simulation has a spectrum that vacillates between perfect transparency to perfect opacity, and does so every fraction of a micron on the wavelength scale. As a result of this vacillation, a gas cell will absorb none of the radiation at a particular wavelength, or all of it. When we look at the fraction of black-body radiation that passes through a cell, this fraction is a constant property of the cell, regardless of its temperature or pressure. We call it the transparency fraction in the CC8 program, and here we will call it τ.

By the principle of radiative symmetry, each gas cells will radiate heat at the same wavelengths it absorbs. But because all the cells around it have the same absorption spectrum, none of the heat radiated by a cell will escape into space, except for the heat radiated by the cells in the top row, which we call our tropopause. These cells radiate directly into space. The power they radiate is the power that a black body would radiate, multiplied by 1−τ.

The incoming heat from the Sun, meanwhile, passes straight through our atmosphere, because we assume that the gas is perfectly transparent to short-wave radiation. The Sun's heat warms the planet surface, which for the moment we assume is something like sand. The sand heats up rapidly until it is losing heat by radiation and convection at the same rate it is gaining heat by absorption of the Sun's light. Some heat it radiates directly into space. The rest passes into the lower atmosphere and must be transported up to the tropopause by convection, where it is radiated into space.

Bottom Gas Cell Temperature = T_B
Planet Surface Temperature = T_S = T_B
Stefan's Constant = σ = 5.7 × 10⁻⁸ W/m²/K⁴
Emitted Surface Radiation = σ(T_S)⁴
Escaping Surface Radiation = τσ(T_S)⁴
Top Gas Cell Temperature = T_T
Emitted Tropopause Radiation = σ(1-τ)(T_T)⁴

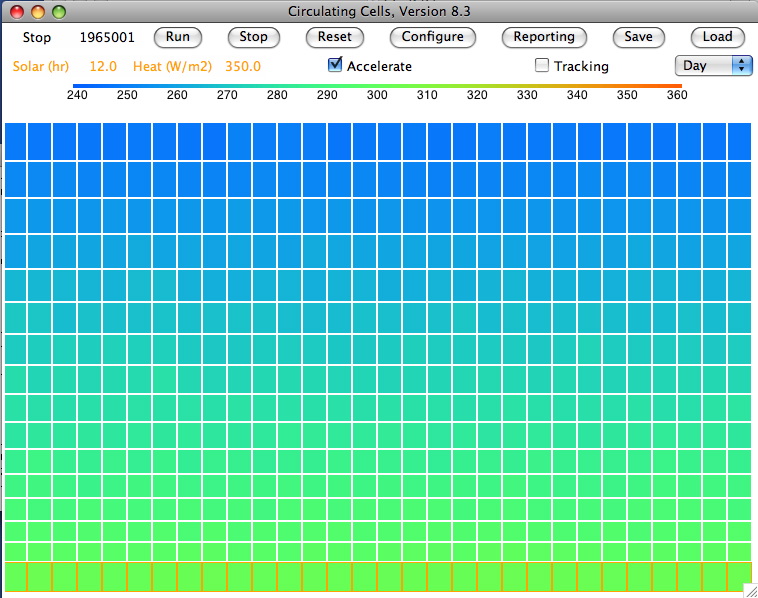
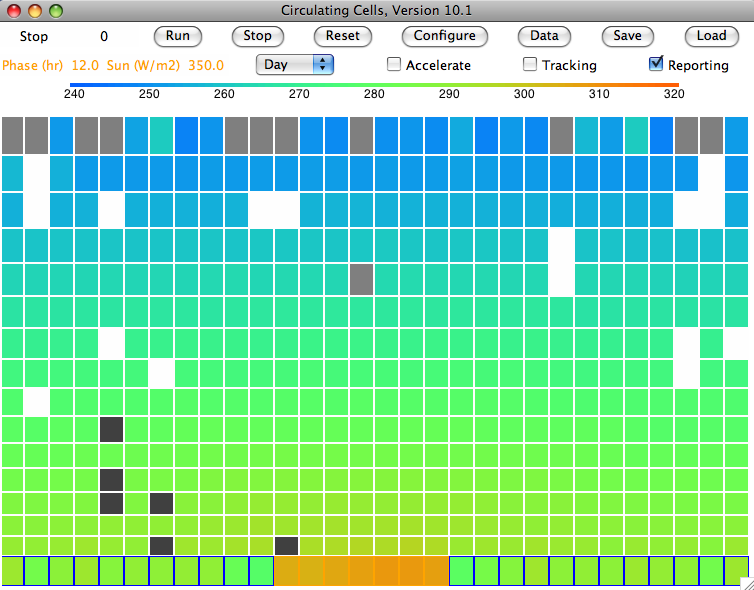
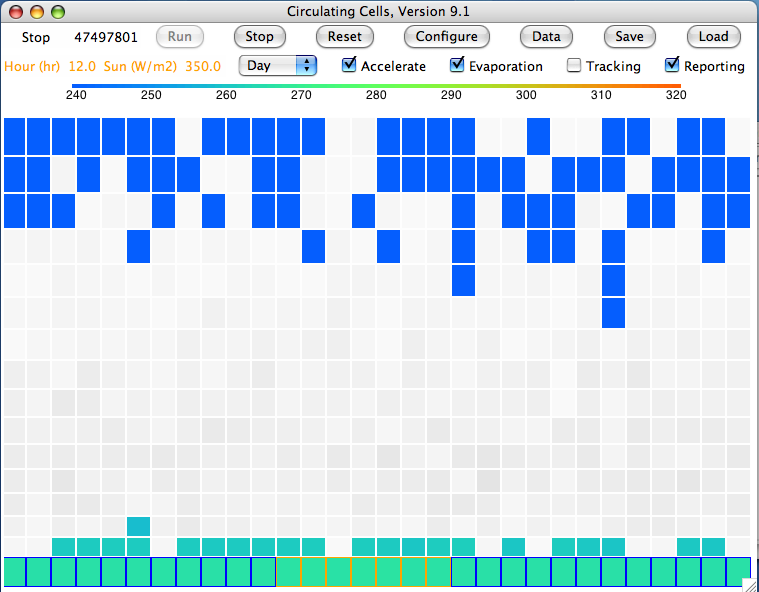
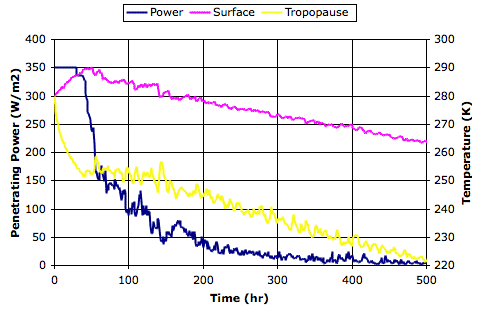
We set τ=0.50 and ran CC8 with Day heating and the Sun's power set to 350 W/m². After ten million iterations we are confident that we have reached equilibrium, and we obtain this array. The average temperature of the bottom cells is 301.1 K (28°C) and of the top cells is 252.1 K (−21°C). The heat radiated by the surface is 468.5 W/m², of which 234.2 W/m² escapes directly into space. That leaves 115.7 W/m² of the Sun's heat to be transported up through the atmosphere. The heat radiated by the tropopause is 115.1 W/m², leaving 0.7 W/m² unaccounted for, which is well within the range of our rounding errors and the random fluctuations in our cell temperatures.

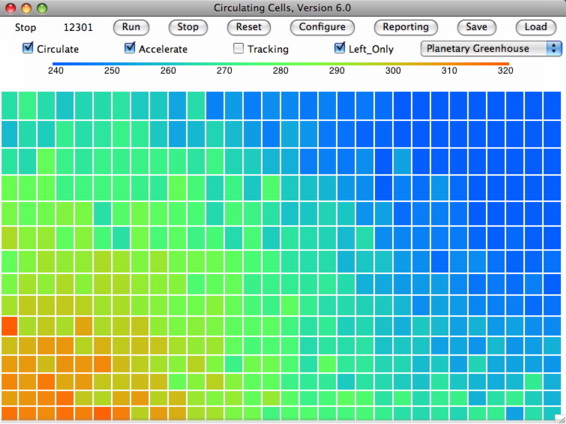
In our previous post, we ran our simulation for an opaque atmosphere, which corresponds to τ=0.00, and the surface temperature rose to 355 K (59°C). We see that τ=0.50 allows the surface to cool by 31°C to 28°C. In With 660 ppm CO2, we showed that doubling the CO2 concentration in the Earth's atmosphere will cause a 2% drop in the total escaping power. So now we set τ=0.49, so as to cause a 2% drop in the power escaping directly from our simulated planet surface into space. We arrive at a this array, in which the surface has warmed by 0.9°C to 302.0 K and the tropopause has warmed by 0.4°C to 252.5 K.

As a check, we run with τ=1.00, in which case the atmosphere is perfectly transparent and the surface radiates all its heat directly into space. The surface cools to 280 K (7°C). The atmosphere assumes the dry adiabatic lapse profile. But now we turn on the cell mixing by setting the mixing fraction to 0.2, and after a few hundred thousand iterations we see the entire atmosphere warm up to 280 K. This is the warm atmosphere we described in our original Greenhouse Effect post and again in Adiabatic Magic. When the atmosphere is not transporting heat to the tropopause, there is no greenhouse effect, and the atmosphere mixes until it arrives at a uniform temperature equal to the surface temperature.

We see that CC8 can simulate the effect of changing the concentration of a greenhouse gas like CO2, simply by making small changes to its transparency fraction. Once we have included evaporation, clouds, and rain into our simulation, we will be able to estimate the effect of changes in CO2 upon the average temperature of our planet surface.

Black-Body Tropopause

Our CC7 program provides six different ways to heat the atmospheric cell array. In CC8, we eliminate most of these and replace them with only three: Day, Night, and Cycle. The others were useful in checking the performance of the simulation, but are no longer necessary. Because we now have a good understanding of the relationship between simulation time, impetus for circulation, and program iterations, we are now able to express the Sun's heat in W/m² instead of the less realistic K/iteration of our earlier programs. We represent the incoming solar power with Q_sun instead of the previous Q_heating. Furthermore, we can use Stefan's Law directly upon the top cells, as if they were black and the gas above them were transparent. Our program now contains a value for Stefan's Constant, which we set to 5.7×10⁻⁸.

For our convenience, we display the time of day in hours in the main window. Time 12.0 hr is noon, when the Sun is certain to shine, and midnight is 0.0 hr. We display the current solar power in W/m². Previously, we applied a sinusoidal variation in the Sun's power during the day, but now we simply turn the Sun's power on to Q_sun during daylight hours, and to zero during the night. As before, however, the Sun will shine for a fraction of the day given by day_fraction.

We run the program with Day heating and the Sun's power set to 350 W/m². We have ke_fraction at 0.0 and we un-check left_only. Our cells have mass 333 kg/m². Their specific heat capacity at constant pressure is 1 kJ/K. Thus the lower cells warm up at 0.001 K/s, which matches our previous Q_heating of 0.001 K/iteration. We allow the array to reach equilibrium, which takes a long time: five million iterations, or one hours on our lap-top. You will find the equilibrium state in Day_1.txt. You can load it into CC8 with the Load button. At equilibrium, the top row's average temperature is 280.0 K. Applying Stefan's Law, the top cells should radiate 350 W/m², which is what we expect, since that's what we are putting in. The surface cell average temperature is 335.4 K, giving us the 55-K drop from the surface to the tropopause. This drop is consistent with our previous results.

We run the program with Q_sun set to 700 W/m² and Cycle heating to simulate day and night. We have day_fraction set to 0.5. After a million iterations we see the temperature of the bottom and top rows varying by a few degrees during night and day, as we did in Rotating Greenhouse.

The equilibrium surface temperature of 59°C (335 K) is much hotter than the surface of the Earth (around 14°C), even though 350 W/m² is the average power of the Sun. The Earth is cooler because its surface and lower atmospheric layers are able to radiate almost half their heat directly into space, assuming there is no cloud cover (see Total Escaping Power and subsequent posts).

Our next step is to allow the surface cells to radiate directly into space, and we will see how the surface cools down as a result. We must implement the surface and tropopause radiation before we can model the effect of clouds.

Cells with Momentum

We invite you to download Circulating Cells 7 by clicking here. Each cell now has vertical and horizontal kinetic energy in the manner we described in Cell Kinetic Energy.

The preservation of momentum after a circulation is controlled by the ke_fraction parameter. By default, this parameter is 0.0, and the simulation will run exactly as before, with the entire impetus for convection being transformed into viscous friction. But with ke_fraction set to 0.9, 90% of the impetus for convection will turn into kinetic energy.

In version 7.0, we have have no graphical illustration of the cell kinetic energy. Perhaps we can use short lines within the cells to indicate momentum in the future. But we can always can stop the simulation and save the array to a text file. The text file tells us the state of each cell. Text files written by 7.0 have a new format, as shown below. But please note that 7.0 can read in text files written by previous versions of the simulation.

row column marking temperature vertical_ke horizontal_ke

In the future, we will add moisture content and cloud concentration to this list of properties. For now, the cells remain dry. The kinetic energy is in units of J/kg, so if we want to know how fast the cell is moving, we take the absolute value of the kinetic energy, double it, and take the square root. If the energy is 32 J/kg, the speed is 8 m/s. The direction is given by the sign of the kinetic energy: positive is up or right.

We have been playing around with CC7, using the Left-Only and Planetary Greenhouse. We set ke_fraction to 0.9 and looked to see if a breeze developed along the lowest row of cells, from right to left. After several hundred thousand iterations, we saved the array to disk and find that all the cells along the bottom row are moving to the left, while all the cells along the top row are moving to the right. By marking cells, we can observe these movements as the simulation runs. We don't see a simple clockwise rotation: there is a lot of random movement on top of the rotation. In the middle rows, the cell movements are as random as they were in our original Left-Side Only simulation with no accounting for momentum. But along the surface and along the tropopause, we appear to have the prevailing breeze we were looking for.

What we have yet to determine is what value of ke_fraction is required to establish a steady breeze, and what fraction is realistic. We invite you to download the code and play with it yourself. We hope the implementation of kinetic energy is correct, but if not we hope you will point out any problems.

UPDATE: There is a flaw in the way we combine cell kinetic energy with impetus for circulation. When we subtract the kinetic energy of a cell from the impetus, this kinetic energy ends up disappearing from the array. We observed a similar program-induced loss of energy in Work by Circulation. Given that the effect of preserving cell momentum was not dramatic, we resolve to remove the kinetic energy calculation from our code, so that ke_fraction will remain zero.

Cell Kinetic Energy

When a block of four cells rotates within our Circulating Cells simulation, the rotation does work, and we call this work the impetus for circulation. We express the impetus for circulation in units of energy per kilogram of gas in the four cells (J/kg). In our CC6 program, we take the impetus for circulation and add it back into the gas as heat. Our assumption is that the impetus is first used to accelerate the gas, and so turns into kinetic energy, but later is dissipated as viscous friction. At the end of our circulation, the gas is once again at rest.

But clearly the gas will not be at rest at the end of a circulation. Once it starts moving, it will tend to continue moving. In our previous post we showed that the cells coming to stop means that our simulation will never allow convection to produce a steady breeze. We would like our simulation to allow a cell to retain some of its kinetic energy after the circulation is complete, and thus allow this kinetic energy to influence subsequent movements of the same cell.

We propose that our upcoming CC7 program should handle kinetic energy in the following way. First, we give each cell two additional numbers that specify its kinetic energy per kilogram in the vertical and horizontal directions. When a cell is moving down, indicate its downward motion by giving its vertical kinetic energy a negative sign. When moving to the left, we give its horizontal kinetic energy a negative sign. The kinetic energy is in units of J/kg, just like the impetus for circulation. The use of a sign to indicate direction does not imply that the kinetic energy is really negative, because kinetic energy cannot be negative.

When four stationary cells rotate, we calculate the impetus for circulation just as we did in CC6. We rotate the cells if the impetus exceeds our impetus threshold. After that, we take a fraction of the impetus, given by the new ke_fraction parameter, and add it to the kinetic energy of each cell. In a clockwise rotation, the bottom-left cell acquires upward kinetic energy, the top-left cell acquires rightward kinetic energy, and so on. What is left of the impetus, we add into the cell temperature as viscous heat. If we set ke_fraction to zero, the simulation will run exactly as it did in CC6, because the entire impetus will turn into viscous heat, and no kinetic energy will be imparted to the cells.

When four cells with kinetic energy rotate, however, we add to the impetus for circulation whatever kinetic energy the cells might have in the direction they will be expected to move.

Suppose we have four cells, three of which are stationary, but the bottom-left one is already moving upwards with kinetic energy 40 J/kg. If the impetus for circulation due to buoyancy and expansion is 2 J/kg, we now add 10 J/kg to account for the fact that the bottom-left cell has 40 J/kg of kinetic energy that favors the rotation. The total impetus is 12 J/kg. Assuming our threshold is below 12 J/kg, the rotation takes place. If our ke_fraction is 0.5, each cell ends up with 6 J/kg in the direction of the rotation. The bottom-left cell ends up with 6 J/kg of upward, vertical kinetic energy, which is far less than the 40 J/kg it started with. Its kinetic energy was used to drive a circulation that might not have taken place at all, and in doing so, the it accelerated and heated three other cells. The bottom-left cell slowed down, but it is still moving up.

If the bottom-left cell also has kinetic energy in the horizontal direction, we ignore this fact, and assume that this horizontal energy will neither hinder nor help the rotation. When the rotation takes place, the kinetic energy of the bottom-left cell in the horizontal direction will remain unchanged.

This is what we plan to do in CC7. We welcome your comments before we proceed. The program is likely to slow down, so we are trying to figure out how to make the calculations faster. Not that any of us is in a hurry, of course.

Left-Side Only

On a sunny day at the beach, the wind tends to blow towards the shore. The land warms up more than the water and warm air rises off the land. The air moving upwards sucks air sideways off the water to make the on-shore breeze. We wonder if our simulation will do something similar if we heat cells only on the left side of the array. The left-side would simulate land, and the right side would simulate water. We might see cells moving along the surface from the right, warming on the left, rising up to the top, and cooling as the move to the right again.

The figure below shows our Circulating Cells simulation program, Version 6.0, which you can download by clicking CC6. With the Left_Only box checked and Planetary Greenhouse heating, the surface cells on the left side receive twice the normal heat from the sun, while those on the right side receive none at all.



We started the simulation by loading the equilibrium state of the array with both sides receiving heat, which we have saved in PGH_Q001_M00. Following our recent discussion of enthalpy, we recognize this symmetric equilibrium state as the one in which all cells have the same enthalpy. Those at the top have more gravitational potential, but less internal heat and pressure energy, so that the sum of all three forms of energy is the same for all cells, or almost the same.

We checked the Left_Only box and increased Q_heating 0.01 K/s. You may point out that the unit of Q_heating should be Kelvin per iteration, not Kelvin per second, but we recall that one iteration corresponds to one second, so the two are equivalent. With Q_heating at 0.01 K/s, the left-side surface cells warm at 0.02 K/s and those on the right do not warm at all.

We ran the simulation for a million iterations and saved the cell array in PGH_Left_Only. The figure above shows the saved state of the cell array, after another ten thousand iterations. The temperature profile is consistent with a large-area circulation of air powered by heating on the left surface. The heated air rises to the tropopause and moves over to the right side as it radiates its heat into space. Once it has cooled, it descends to the right surface and moves along to the left.

We marked a few cells by clicking on them, and watched them go around. We invite you to do the same. The cells circulate in a clockwise direction. They rise to the tropopause on the left, but hardly ever rise to the tropopause on the right. Nevertheless, we don't see individual cells moving steadily in a clockwise direction across the width and height of the array. Often, cells rise on the extreme left and descend upon the center-left. Cells on the right rise up a little and fall again. They slowly drift to the left, but they do a lot of jumping around along the way.

When averaged over thousands of iterations, the combined movement of the cells is a large clockwise circulation, with a net movement of cells from right to left along the surface. But a simulated person standing on the center surface would not feel a steady breeze blowing from the right side. He would instead feel the wind changing every minute or two, and only by looking at the average wind speed would he be able to conclude that the net movement of air was on-shore.

Our simulation assumes that all momentum generated by circulation is dissipated as viscous heat at the end of each circulation. Thus each circulation affects only the temperature of the cells. No cell can build up momentum that encourages further circulation in the same direction.

We conclude that momentum is one of the driving forces behind the on-shore breezes. Buoyancy alone is not sufficient. If we want our simulation to produce steady winds, we must allow circulating cells to retain some of the momentum they gain during circulation, and we must allow this momentum to influence future circulations of the same cell.