Slow-Sinking Clouds

In Falling Droplets, we concluded that 10-μm water droplets will sink at 3 mm/s in air at pressure 100 kPa. The lowest atmospheric cells in our Circulating Cells program are at 100 kPa, and they are roughly 300 m high, so we see that it will take a hundred thousand seconds for a droplet to fall the height of the cell. Cells higher up are taller, but the gas within them is thinner. A droplet must fall more quickly through thinner air before its weight is matched by air resistance. For simplicity, we will assume that the time it takes a 10-μm droplet to fall the height of a cell is the same regardless of altitude.

As we found in Simulation Time, our program checks each gas cell every one hundred iterations on average, which corresponds to every 100 s. If it takes a droplet one hundred thousand seconds to fall the height of a cell, and the droplets in the cell are evenly distributed, 0.1% of the droplets will sink out of the cell every 100 s. If the cell rests upon a surface block, these droplets will return to the surface. We now have a way for water to leave the surface, by evaporation, and a way for water to return to the surface, by sinking. If the gas cell rests upon another gas cell, the droplets enter the cell below, where they may evaporate.

In Circulating Cells Version 9.1, we specify the sinking speed of droplets at 100 kPa with sinking_speed_mps in units of meter per second. We set sinking_speed_mps to 0.003 m/s and loaded CS_0hr into our array, which is the starting condition we used in Cold Start.

The planet warms quickly in the steady light of the Sun. After two hundred hours, the atmosphere is full of clouds and the planet starts to cool. The clouds sink towards the surface. After four thousand hours, they are thin enough that the sun starts to warm the surface. After eight thousand hours, this warming is stopped by the formation of new clouds. After a thirty thousand hours, the atmosphere settles to the steady state shown below, which you will find saved as a text array here.



The graph below plots temperature and cloud depth versus time for the first thirty thousand hours.



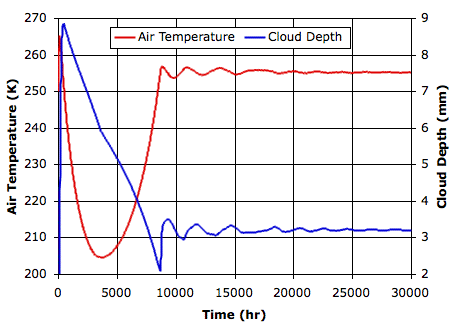
After thirty thousand hours, the sand and water surfaces are both at 260 K (−13°C), and the lower gas cells are at 255 K (−18°C). The average cloud depth is 3.2 mm and the average power reaching the surface is 120 W/m².

The combination of evaporation and sinking gives rise to an equilibrium in which the clouds allow just enough heat to reach the surface so that evaporation balances the return of water to the sea in the form of sinking droplets. This balance between evaporation and sinking controls the temperature of the planet surface. In our next post, we will increase the sinking speed by a factor of a hundred and see how this affects the surface temperature. We expect the surface temperature to go up, because only then will evaporation keep up with the increased loss by sinking.

UPDATE: It turns out that our code was allowing clouds to sink only when they took part in a circulation, which resulted in them sinking roughly a hundred times slower than they should have, so our effective sinking rate in this simulation was more like 0.03 mm/s. When we correct our error, so that the clouds really do sink at 3 mm/s, the surface temperature warms by roughly 7 K. [07-JAN-12]