Vapor Versus Liquid

In our last post, we concluded that the first 100 m of the Earth's atmosphere would absorb all radiation from the Earth's surface. To arrive at this conclusion, we used the well-known absorption spectrum of liquid water, and applied it to water vapor. If the absorption length (or penetration depth) of 10-μm infrared in liquid water is 20 μm, then the absorption length in water vapor a million times less dense will be a million times greater, or 20 m.

We brought this up with an astronomer friend, and he pointed us to the following graph of predicted absorption of infrared light from outer space by the atmosphere above an infrared telescope on Mauna Kea in Hawaii. We obtained the plot here.



According to the authors, the graph assumes the equivalent of 1 mm of liquid water distributed as water vapor in the air above the telescope. Our graph of absorption length in water gives us an absorption length of around 10 μm for 11-μm infrared. Other peoples graphs show the same thing. If we put a 1-mm layer of liquid water above the telescope, the water would absorb 99.995% of infrared arriving from outer space.

But the graph above appears to predict 98% of 11-μm infrared to reach the telescope from outer space. In other words, the graph suggests that our estimate of absorption by water vapor is off by a factor of a thousand. So we are trying to figure out why the predictions of astronomers (who we trust) are so at variance with our own back-of-the envelope calculations (which we sort of trust).

One possible explanation for the difference is that the behavior of water molecules in water vapor is dramatically different from that of water molecules in liquid water. Sites like this one discuss the difference between water vapor and liquid water, but their graphs appear show water vapor absorbing more than liquid water.

Any advice on this matter would be most welcome. We are looking into it.

UPDATE: The absorption spectrum of water vapor is the spectrum of free water molecules. The molecules vibrate in symmetric and clearly defined ways. The absorption frequencies are sharply-defined. In liquid water, the vibrations are influenced by bonds between molecules. These bonds, called hydrogen bonds occur between the slightly positive hydrogen atoms of one molecule and the slightly negative oxygen atoms of another molecule. The hydrogen bonds serve to spread the absorption wavelengths so that they blend together, giving a black liquid at all infrared frequencies. Water vapor, on the other hand, absorbs in narrow bands that do not always overlap, so that there are bands in which the water is not black at all. Indeed, there are windows in the spectrum, where water vapor is transparent.

For a graph of atmospheric transmission including water vapor and carbon dioxide, take a look at page two of this SOPHIA paper. For a seminal paper on water vapor absorption see Elsasser.

Earth Radiator

Following our discussion of black bodies and our calculation of solar heat, we now consider whether or not the Earth acts as a black-body radiator.

In an earlier graph we show how a body at 200 K (−70°C) radiates at infrared wavelengths 6 μm to 60 μm. In another graph we show how a body at 300 K (27°C) radiates at infrared wavelengths 4 μm to 40 μm. In Radiative Symmetry we showed that any particular object must emit and absorb any particular wavelength with equal efficiency. The extent to which the Earth is a black-body radiator at infrared wavelengths between 4 μm to 60 μm is the extent to which it is also a black-body absorber at these same wavelengths.

The Earth's atmosphere contains water droplets in the form of clouds, and also gaseous water in the form of water vapor, which we experience as humidity. As we showed in an earlier experiment, liquid water is black to infrared wavelengths. The following graph plots the absorption length of liquid water with wavelength. The data comes from three papers, Irvine et al, Sullivan et al, Hale et al, and Zolotarev et al, as provided here. We converted "absorption coefficient" in cm⁻¹ into "absorption length" or "penetration depth" in μm.





The absorption length or penetration depth, L, is the depth of water required to absorb 63% of incident radiation. We have A = 1 − e ^x/L, where A is the fraction absorbed and x is depth. (See here for another source of same plot, thanks to Teddy Cheung for link.) After depth 3L, absorption is 95%. As you can see from the graph, the largest value of L for wavelengths 4μm to 60μm is 80μm. Water 240 μm deep absorbs over 95% of all radiation between 4 μm and 60 μm.

Water droplets in clouds are roughly twenty microns in diameter, so each droplet absorbs a significant proportion of infrared radiation. We conclude that clouds are opaque to infrared. But what about water vapor? The following plot, provided by NASA, shows water vapor content by volume with altitude and latitude in the Earth's atmosphere. The color-coding is logarithmic. Light green corresponds to roughly 1 g/m³ (one gram per cubic meter). Black is missing data.





The atmosphere up to altitude 3 km contains at least 1 g/m³ water vapor for all latitudes. Liquid water has density 10⁶ g/m³. Radiation passing through air encounters one million times fewer water molecules per meter than air traveling through water. Suppose we assume a simple linear relationship between the concentration of water molecules and the absorption length. In that case, the absorption length of 1 g/m³ water vapor would be one million times longer than that of liquid water because the concentration of water molecules is one million times lower. Radiation must travel one million times farther in order to encounter as many water molecules as it would in pure water. Thus 240 μm of liquid water would have the same absorption as 240 m of air containing 1 g/m³ of water vapor. A 10-m thickness of the Earth's humid, lower atmosphere would absorb over 95% of infrared radiation between 4 μm and 60 μm.

But our astronomer friends tell us they can see through the atmosphere at infrared wavelengths. Our assumptions about water vapor cannot be correct. We will investigate the absorption spectrum of water vapor in future posts. The Earth's oceans, however, are made of liquid water, and they cover most of the globe. A thin layer of liquid water absorbs all infrared wavelengths. By the principle of radiative symmetry liquid water must be an efficient radiator of infrared wavelengths as well. Whether water vapor absorbs much infrared radiation or not, the Earth will be a good black-body radiator.

Solar Heat

The surface of the sun is at roughly 5800 K. The center of the Sun is much hotter than the surface. The surface is cooler because it radiates its heat, and so draws heat out from the center in a manner reminiscent of the greenhouse effect. Very hot objects tend to act as black bodies, and radiate according to Stefan's Law. Even a piece of polished steel will turn black and start to glow when it reaches 2000 K. As a black body at 5800 K, the Sun radiates 64 MW/m². Its radius is 700,000 km, so its total heat output is 4.0×10²⁶ W.



The Earth orbits the Sun at 150,000,000 km and has radius of 6,400 km. It presents a circular area to the Sun's radiation of 1.3×10¹⁴m² . When it reaches the Earth, the Sun's radiation is spread out across a sphere of the same radius as the Earth's orbit, and so has intensity 1.4 kW/m². The solar heat absorbed by the earth is 1.8×10¹⁷W.

Suppose the Earth itself were a black body. As a black body, it absorbs all heat landing upon it from the Sun. Either it radiates all this heat into space or it doesn't. If it doesn't, it gets warmer. If it gets warmer, it will radiate more heat, according to Stefan's Law. The Earth will eventually get warm enough that it radiates all the heat it absorbs from the Sun. We assume the Earth has already been through this warming process, and is radiating as much heat into space as it receives from the Sun.

The surface area of the Earth is 5.1×10¹⁴m². If the Earth were a black body, it would radiate the solar heat it absorbs when it was at 280 K, or 7°C. In our diagram, we show how all terms in our calculation cancel out, except for the temperature of the Sun, T_s, the radius of the Sun, r_s, and the radius of the Earth's orbit, r_o, resulting in a simple formula. Using this formula, we also arrive at 280 K for the Earth's radiating surface temperature.

As it is, the average temperature of the Earth's surface is 287 K, or 14°C. At first glance, the Earth appears to behave like a black body. But is it really?

ASIDE: The Sun delivers 1.8×10¹⁷W to the Earth, and the Earth's surface area is 5.1×10¹⁴m², so the average power received from the sun at the Earth's surface is 350 W/m². (Well, its 353 W/m² with our numbers, but we have rounded to two significant figures.)

Black Bodies

All objects that are above absolute zero temperature tend to radiate heat. The maximum amount of heat, P_BB that a body at temperature T can radiate per square meter of surface area is given by Stefan's Law.

P_BB = 5.7×10⁻⁸ T ⁴

(Note: Here we measure T in Kelvin, K. We have 0 K = −273°C and 0°C = 273 K. At 0 K an object has no heat at all, and therefore radiates no heat. The constant has units W/m²K⁴)

A body that radiates this maximum amount of heat is a black body. Such a body will radiate its power at a range of wavelengths as given by Plank's Law. The graph below shows the distribution of radiated power with wavelength for black bodies at 6000 K, which is the approximate temperature of the surface of the Sun, and 200 K, which is about as cold as it ever gets on the surface of the earth. The vertical axis is normalized power density, which we obtain by taking the power density at each wavelength and dividing by the maximum power density. The power density for a small range of wavelengths λ to λ+δ is the power radiated within this small range divided by the width of the range, δ, and so has units W/m²/m. Note that the wavelength axis has units μm but is plotted with a logarithmic scale.



An object at 6000 K radiates 810,000 times as much power per square meter as an object at 200 K (−73°C). The graph shows how the 74 MW/m² emitted by an object at 6000 K and the 91 W/m² emitted by an object at 200 K are distributed with wavelength. The wavelength of greatest power emission is proportional to temperature, according to Wein's Displacement Law.

λ_max = 2.9×10³/T m.K

In Radiative Symmetry we showed how the Second Law of Thermodynamics dictates that a body's efficiency as a radiator at any particular wavelength is exactly matched by its efficiency as an absorber at that same wavelength. When a body absorbs all radiation of a particular wavelength we say it is black to that wavelength. A body that is black to a particular wavelength will radiate as much heat as a black body at that wavelength. A body that is transparent to a particular wavelength will radiate no power at that wavelength. A body that reflects half of a particular wavelength will emit half as much power as a black body at that wavelength.

The graph above shows that the peak emission wavelength for a body at 6000 K is 0.5 μm (green light), and for a body at 200 K is 15 μm (infrared). Almost all the power emitted at 6000 K lies between 0.2 μm (ultraviolet) and 2 μm (near infrared), and at 200 K lies between 6 μm (infrared) and 60 μm (far infrared).

If we want to determine graphically the proportion of power radiated in two or three different wavelength bands, we can count squares under a linear plot of power density, such as the one below for 6000 K, which is sunlight. You will find a similar plot for atmospheric temperatures here.



Visible light lies in the range 0.4 μm (royal blue) to 0.7 μm (ruby red). Counting squares under the graph, we find that roughly 15% of sunlight's power is in the ultraviolet, 40% is visible, and 45% is in the infrared.

In our next post we will consider how the atmosphere absorbs radiation from the earth but is transparent to radiation from the Sun, leading to the greenhouse effect.

The Greenhouse Effect

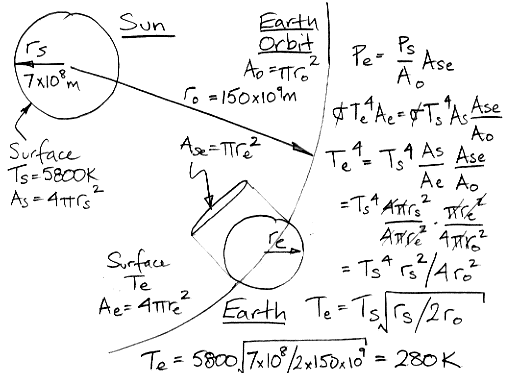
When we wrote the first draft of this post, every explanation for the greenhouse effect that we had found on the web contradicted either the second law of thermodynamics, or the laws of black body radiation, or our own laboratory experiments. At first we thought these contradictions meant that the greenhouse effect did not exist, and we were not alone in coming to this conclusion. Our initial title for this post was "Refutation of the Greenhouse Effect". But we were mistaken. The greenhouse effect is a simple phenomenon that occurs when we have the correct planetary surface and atmosphere.

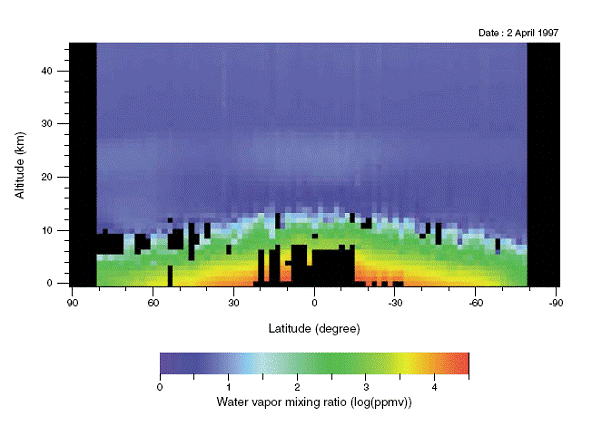
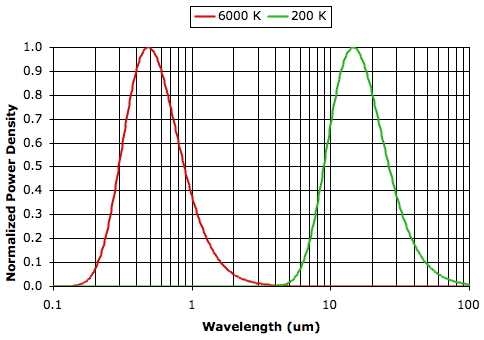
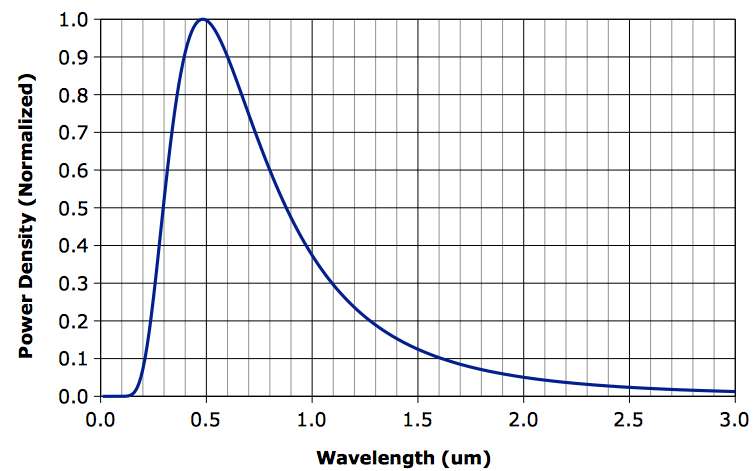
The greenhouse effect is the "heating of the surface of a planet or moon due to the presence of an atmosphere containing gases that absorb and emit infrared radiation." In the context of the theory, these gases are called greenhouse gases. In the case of Earth's atmosphere, the greenhouse gases include water vapor, carbon dioxide, and methane. As we described in A Radiation Experiment, most of the heat arriving from the Sun is of wavelength less than 2 μm, while most of the radiation emitted by the Earth is of wavelength greater than 2 μm. Greenhouse gases, water vapor in particular, absorb a small fraction of the radiation arriving from the Sun, but a large fraction of the radiation emitted by the Earth.

Suppose the atmosphere consisted only of nitrogen, oxygen, and argon. These gases are transparent to both the Sun's and the Earth's radiation. As we showed in Radiative Symmetry, transparent gas cannot radiate heat. So an atmosphere of nitrogen, oxygen, and argon would not radiate heat. There would be no radiation of heat into space by the upper atmosphere. Without such radiation, the atmosphere would be calm and still, and its temperature uniform.

Suppose we now add greenhouse gases to the atmosphere. These gases provide a means for the atmosphere to radiate into space the heat it acquires from the surface of the Earth. Convection is the dominant source of atmospheric heating near the Earth's surface. But radiation is a significant source of heat transfer between layers of the atmosphere. The Second Law of Thermodynamics dictates that all gases are exactly as effective at radiating heat as they are at absorbing heat. The Second Law further dictates that no gas can distinguish between the heat it acquired by absorption of radiation and the heat it acquired by convection. Because of greenhouse gases, a packet of air in the upper atmosphere radiates heat into space. It cools. As it cools, it becomes more dense. It sinks back to Earth. A new packet of warm air rises to take its place. As air rises, it expands and cools, but it is the cooling by radiation at the top of the atmosphere that drives the circulation of air between the lower and upper atmosphere. This radiating atmosphere is turbulent and cooler at the top than the bottom.

Suppose we warm a brass disk with an incandescent lamp and cover the disk with a film of water that cannot evaporate. Does the water film cause the disk to warm up or cool down? In A Radiation Experiment and The Cling-Film Diaper we showed that the disk cools down. It cools down because the water film is a far more effective infrared radiator than brass. Water vapor is also an effective radiator of infrared, and there is plenty of water vapor in the Earth's atmosphere. If the Earth were made of brass, water vapor in the atmosphere would allow the Earth to radiate heat more effectively, and so would act to lower the temperature of the Earth, not warm it up. But the Earth is not made of brass. Two thirds of it is covered with water. Unlike brass, the oceans are excellent radiators of heat.

Consider a planet, such as the Earth, that is covered for the most part with oceans and yet somehow, for the sake of argument, has an atmosphere that is transparent to both the sun's and the ocean's radiation (that is to say, the atmosphere contains no water vapor, despite being covered with water). The ocean will warm up in the light of the sun until it reaches a certain temperature, T_t. The atmosphere will warm up to the same temperature through its contact with the ocean. At this temperature, the ocean is radiating as much heat as it receives from the sun. The atmosphere, being transparent, radiates no heat. The upper regions of the atmosphere do not radiate heat. They do not cool down. The atmosphere's temperature is uniformly T_t, and the atmosphere is calm.

We now add water vapor to the atmosphere, which will occur naturally through evaporation from the oceans, provided T_t is high enough. And let us assume, again for the sake of argument, that there are no clouds formed from this water vapor, even though this is an unrealistic assumption. The water vapor makes the atmosphere opaque to radiation from the ocean, but the atmosphere remains transparent to radiation from the sun. The radiating surface of the planet is no longer the ocean, but the upper reaches its humid atmosphere. It is the upper atmosphere that must be at temperature T_t in order to radiate heat at the same rate that the ocean is absorbing heat from the sun. Of course, the upper atmosphere was already at T_t before we added the water vapor, so its temperature does not change. Now we must consider how the heat that the ocean absorbs from the sun will get to the upper atmosphere, where it can be radiated into space. According to the Second Law of Thermodynamics, the ocean will have to be warmer than the upper atmosphere in order for heat to flow to the upper atmosphere. Thus the ocean warms up to some new temperature T_g > T_t, and it is this warming that is called The Greenhouse Effect.

UPDATE [01-JAN-16] Of course, it is unrealistic to suppose that any atmosphere containing water vapor, and radiating heat into space, will contain no clouds. The warm air rising from the surface of the Earth expands as it rises, because its pressure drops. As it expands, it cools down. As it cools down, its water vapor condense into clouds. A thick cloud can reflect 90% of the sun's radiation. If the Earth were to be covered by thick clouds, its surface would cool dramatically. We calculate it would cool by almost 100°C. But if the Earth cooled by 100°C, there would be very little evaporation from the frozen oceans, and therefore insufficient water vapor in the atmosphere to cover the planet with thick clouds. We see that the Earth cannot be too warm, for it would then be covered by clouds and it would cool down, nor can it be too cold, for it would then have a clear sky and warm up. The result is that the Earth's surface settles to temperature at which cooling by clouds is in equilibrium with warming by the sun and by the greenhouse effect. We explore this equilibrium with calculations and simulations in our later posts.

Cling-Film Diaper

In our first demonstration of radiative cooling by a water film, we applied the water film to the top surface of a brass disk, which we heated from above with a lamp. The experiment requires a thin water film, or else the film will interfere with dissipation of heat by convection, thus slowing down the cooling effect of the film. In this second demonstration, we cover the bottom surface of the brass with a water film, and observe the radiative cooling more easily. We hold the water on the bottom surface of the disk with a diaper made out of kitchen cling-film.



We allow the disk to warm up beneath our lamp. It warms to 49.4°C. We inject water into the diaper. The disk cools to 42°C at first because the water we added was at 42°C. After that, the brass warms up again, reaching a new equilibrium temperature of 47.0°C. The new equilibrium is 2.4°C cooler than the equilibrium without the water film. For a more detailed description of the experiment, see here.

The diaper stops the evaporation of water. Water is a poor conductor compared to brass, so covering the bottom surface with water will only decrease the heat lost by convection and conduction. Water is transparent to the 1-μm infrared radiated by the lamp, but it is black to the 10μm infrared radiated by warm bodies. A black body radiates heat more efficiently than a shiny body. We cover the brass with water and it radiates more heat, so the disk cools down.

And so we obtain the same result again: water acts as a radiative cooler for warm objects that are heated by visible and near-infrared light.

Radiation Experiment Results

The photograph below shows the apparatus we used in A Radiation Experiment.



The table below gives the equilibrium temperatures we obtained with various disk covers, water layers, and lamp covers. For more details, including annotated graphs of temperature versus time, see here.



Here are two highlights from the results. First, a 100-μm film of water on the top surface of our brass disk, contained beneath a cover of kitchen cling-film so that it cannot evaporate, causes the disk to cool by 1.7°C. The water film is a far more efficient radiator than shiny brass. Second, we observe negative feedback during the radiative cooling. Most of the heat from the lamp leaves the disk by convection through the top surface, so as the water film cools the top surface by radiation, the convection slows down, and heat is held back inside the disk. As a result, we see a gradual decline in temperature instead of a first-order exponential step. (You can see this decline after Point 10 in this graph.) The negative feedback, and the fact that a thicker film of water acts as a thermal insulator, make our observation of radiative cooling at the top surface hard to perform. With cling-film and a syringe, we can now reproduce the effect at will. But a better choice would be to coat the bottom surface of the brass with water, and that's what we will do next.

Nevertheless, what we have shown is that a water film cools down an object that is being heated by visible and near infrared light, but which is itself a poor radiator of far infrared. We have also shown that simple systems like our brass disk and lamp can exhibit negative feedback.

A Radiation Experiment

We say an object is perfectly black if it absorbs all electromagnetic radiation that lands upon it, regardless of wavelength. As we showed in Radiative Symmetry, a perfect absorber is also a perfect radiator. Black bodies radiate more heat per unit surface area than any other type of body.

Hotter bodies radiate heat using shorter wavelengths. The graph below shows the distribution of radiated power with wavelength for black bodies at 300 K and 3000 K.



The absorption spectrum of water is such that a 20-μm film of water will absorb 95% of the heat radiated by a black body at 300 K, but less than 1% of the heat radiated by a body at 3000 K. Room temperature is roughly 300 K. An incandescent lamp filament reaches roughly 3000 K.

We took a shiny brass disk and let it warm up beneath an incandescent lamp with various treatments of its top surface. In some experiments, we covered it with a film of water. Sometimes we covered the water with a clear plastic sheet. The plastic is transparent to visible light. It may or may not be transparent to radiation from the disk and the lamp. Sometimes we covered the lamp itself with the same type of plastic sheet. For a more detailed description of our apparatus and procedures, see here.

In each experiment, we record the equilibrium temperature of the brass disk. We will present our results in our next post. In the meantime, we invite you to consider our various arrangements and see if you can anticipate our results.

Radiative Symmetry

In our previous posts (Absorption, Not Reflection and Glass Houses) we showed that heat enters the atmosphere by convection and absorption of radiation, and leaves by emission of radiation.

Let us examine this process of absorption and emission in more detail. Suppose a planet were surrounded by a transparent atmosphere. An atmosphere consisting entirely of oxygen and nitrogen would meet our requirements. Both gases are transparent to visible and infrared light, so they would absorb no radiation from the sun or from the planet. Heat would enter a transparent atmosphere only by convection from the planet's surface.

If heat is to leave this transparent atmosphere, it must do so by radiation. But can a transparent gas radiate heat? Imagine that we put a cubic meter of our transparent gas in a room with reflecting walls (we could use surface-coated mirrors). The cubic meter of gas is contained in a transparent balloon. Also in the room is a large, black box. We suck all the air out of the room with a vacuum pump. At the beginning of our experiment, the gas and the black box are at the same temperature. The black box radiates heat. This radiation passes through the vacuum and the transparent gas, reflects off the walls, and is re-absorbed by the black box.

Now, let us assume that our transparent gas radiates heat. If so, this radiation will be absorbed by the black box. The black box will warm up because is is absorbing the heat it radiates itself as well as the heat radiated by the gas. The gas, meanwhile, must cool down, because it is radiating heat but absorbing none at all, on account of its being transparent. The gas continues to cool down and the black box continues to heat up. Heat is passing, of itself, from one body to a hotter body.

The second law of thermodynamics states that heat cannot, of itself, pass from one body to a hotter body. A transparent gas that radiates heat violates this law. All gases, and indeed all objects, must absorb and emit radiation with the same ease. Any difference between a gas's ability to absorb radiation of a particular wavelength and its ability to emit radiation of the same wavelength amounts to a violation of the second law of thermodynamics.

The second law dictates that a transparent gas cannot radiate heat. The transparent atmosphere around our imaginary planet does not radiate heat. It retains all the heat it acquires by convection from the planet's surface. It continues to absorb heat by convection until the entire transparent atmosphere is at the same temperature as the planet surface, and at that point convection stops and the atmosphere is in thermal equilibrium with the planet surface.

If the atmosphere of the earth were made up only of nitrogen and oxygen, the entire atmosphere, from the troposphere to the exosphere, would be warm.

But the earth's atmosphere is not warm. The surface of the earth has an average temperature of 14°C. The atmosphere at altitude 10,000 m is at around −40°C. The earth's atmosphere is not warm because it radiates heat. It radiates heat because it is not transparent. It is not transparent because it contains carbon dioxide and water, both of which are good absorbers of infrared light, and therefore good emitters of infrared light also.

Glass Houses

In Absorption, Not Reflection we showed that heat leaves the atmosphere almost entirely by radiation. Conduction of heat through columns of air is insignificant compared to radiation absorbed by carbon dioxide and water in the atmosphere.

Heat cannot leave the atmosphere by convection, but it does enter by convection. The ground warms up in the light of the sun. Air in contact with the ground warms up. It becomes less dense, and rises. It is replaced by cool air from above, which soon warms up and rises itself.

Lack of convection is responsible for the warming of greenhouses. Heat from the sun enters the greenhouse and warms the floor. The floor warms the air. But the air cannot rise out of the greenhouse, and so the same body of air continues to warm up.

We demonstrated the greenhouse effect in our laboratory. We used a rock salt crystal as a roof for a black-walled space. We heated the space with a 60-W incandescent bulb. At first, we removed two walls and raised the roof to allow air to flow freely, as shown here. The black-walled space warmed up from 19°C to 26°C (with a few hiccups along the way because we had to replace the bulb). We lowered the rock salt crystal onto the space and added the two remaining walls, as shown here. The air inside the space was trapped. The temperature rose from 26°C to 30.5°C.



We used rock salt because it is transparent to both visible and infrared light. Our 60-W bulb filament is a around 3000 K, with peak emission wavelength of 1 μm. Our black-walled space is at around 300 K, with peak emission wavelength of around 10 μm. Rock salt is transparent to both frequencies. For a more detailed description of our apparatus and methods, see here.

The warmth in a greenhouse is due to the heating of trapped air by the sun. Outside greenhouses, heat enters the atmosphere by convection. Conduction plays a role only at the surface, where air in contact with the ground gains heat by conduction, thus initiating convection.

Absorption, Not Reflection

Carbon dioxide absorbs infra-red light. Infra-red photons are just right for exciting the atomic bonds within the carbon dioxide molecule. After absorbing an infra-red photon, the carbon dioxide molecule vibrates. The molecule is now hotter. That's what heat is: vibration of atoms.

Carbon dioxide does not reflect infra-red light. Nor does it scatter infra-red light. It absorbs infra-red light and warms up.

Our atmosphere contains carbon dioxide, roughly 0.04% by volume. This carbon dioxide absorbs infra-red radiation from the earth and the sun. Some calculations suggest that the column of air above each square meter of the earth absorbs of order 2 W of infra-red radiation from the earth. If we assume that the atmosphere is, on average, losing heat as fast as it is gaining heat, then we must ask ourselves how this 2 W is leaving the atmosphere.

The 2 W might leave by convection, in which warmer air rises. But there is nowhere for the air to go once it gets to the top of the atmosphere, so convection cannot remove the heat from the atmosphere.

The 2 W might leave by conduction, in which molecules collide with their neighbors. But air is a thermal insulator, and a 1-km column of air with a 10°C temperature difference from one end to the other will conduct only 0.0002 W of heat for every square meter of its cross-sectional area.

By elimination, the 2 W must leave the atmosphere by radiation, in which a vibrating atom emits a photon and so loses heat. This photon may be absorbed by the atmosphere before it travels more than a few hundred meters. It may be absorbed by the earth. Or it may escape the atmosphere and propagate into outer space, in which case its absorption will be greatly delayed.

So, heat leaves the atmosphere almost entirely by radiation.

PS. I am going somewhere with this argument, but I'm hoping to build up some suspense along the way.

Add a Heater, Chill the House

A fundamental assumption of the AGW (Anthropogenic Global Warming) hypothesis is that when a new source of heat appears in the atmosphere, the average temperature of the entire atmosphere will rise. In particular, AGW states that increasing CO2 (carbon dioxide) concentration will absorb heat emitted by the earth's surface, thus creating a new heat source in the atmosphere, and this new heat source will cause global warming. As we have said before, this hypothesis has no empirical basis. The hypothesis may sound eminently reasonable, but that's what we demand of a hypothesis: it must be eminently reasonable so that we are motivated to test it. Until we have performed the experiments, however, a hypothesis remains a hypothesis.

The first house I lived in with a real fireplace was in Boston. It was −20°C outside in the winter of 2000. I built a big fire in the living room, telling my children that they would be extra-warm that night, because the fire was going to warm up the whole house. I piled on the wood, until the fireplace was a blaze of flame over a bed of coals. The living room was hot and dry. I was well pleased with my efforts. But when I put the kids to bed, I found that their room was cold, too cold for them to sleep comfortably. Before I lit the fire, their room had been warm.

This outcome was surprising to me, but I have observed the same thing many times since, also in our new house, where we have a wood stove in the living room. Indeed, if I want my children's bedrooms to be warm, I know I have to refrain from lighting a fire in the living room.

Either that, or I have to move the thermostat out of the living room.

The climate is a far more complex system than my house. It may be that more CO2 will warm up the world. On the other hand, it may be that more CO2 will bring about the next ice age. More likely, in my opinion, is that more CO2 will have no measurable effect at all upon the global temperature. I could make a compelling argument for any of these outcomes. But, as we have said already, a compelling argument doth not a scientific theory make.

UPDATE: For our warm-climate readers, see comments for explanation of "thermostat".