Total Escaping Power

Our current approach to modeling the Earth's greenhouse effect is to divide the Earth's atmosphere in to 3-km layers. So far, we have considered how each of the first seven layers absorbs and emits long-wave radiation. Our study of these seven layers has been motivated by a desire to calculate the total heat radiated into space by the Earth and its atmosphere, and ultimately to estimate the strength of the relationship between the Earth's surface temperature and the concentration of CO2 in its atmosphere.

In previous posts, we simplified our discussion by assuming that each atmospheric layer was either perfectly transparent or absolutely opaque at each wavelength. This assumption, combined with an examination of the absorption spectra, allowed us to say that all radiation passing through one layer would be sure to pass through all higher layers as well. Furthermore, our assumption allowed us to ignore the fact that most upward radiation is not vertical, but at some angle to the vertical. Radiation traveling at 60° to the vertical will pass through 6 km of air as it ascends through a 3-km layer, and so is more likely to be absorbed by the layer. But if we assume that the 3-km layer is either perfectly transparent or absolutely opaque, we conclude that radiation of a particular wavelength will either pass entirely through the layer or be entirely absorbed by the layer, regardless of its direction of travel.

Today we present our first layered-atmosphere computer model. The model does not assume that each layer is either transparent or opaque. When we calculate the power escaping into space from layer A at temperature T between wavelengths 10.0 μm and 10.1 μm, we proceed as follows. We start with the black-body radiation power density at wavelength 10 μm and temperature T. This power density is almost constant in the narrow range 10.0 μm to 10.1 μm, so we multiply the power density at 10.0 μm by 0.1 μm and obtain a good estimate of the power radiated between 10.0 μm and 10.1 μm. Now we multiply this power by the fractional absorption of layer A at 10.0 μm. The principle of radiative symmetry dictates that the efficiency with which a body emits radiation at a particular wavelength, as a fraction of the power emitted by a black body, is exactly equal to the efficiency with which it absorbs that same wavelength. So we now have the power radiated by layer A between wavelengths 10.0 μm and 10.1 μm. By assumption, whatever is not absorbed by the layer above A will escape into space, so we multiply the power radiated by A by the fractional transmission at 10.0 μm (that's one minus the fractional absorption at 10.0 μm) of the layer immediately above, and so arrive at the power between 10.0-10.1 μm that escapes from layer A into space.

To obtain the total power escaping into space from each layer, we add up the power escaping in all the 0.1-μm bands from 5 μm to 30 μm, which is the extent of our absorption spectra. We will include the surface of the Earth as its own layer. As we have in the past, we will assume the Earth's surface is a black-body radiator. Thus our program will calculate for us the total power escaping from the Earth into space, and allow us to see how much of this power is radiated by the surface and by each atmospheric layer.

Although we have dropped the transparent-opaque simplification, we retain two of its corollaries. First, we ignore the fact that most upward radiation is not vertical. Second, we assume that any radiation that manages to pass through the layer immediately above will be sure to pass through all remaining layers. These assumptions will effect our estimates, but we believe the effect will be less than 10%. In the future we may enhance our model to remove these assumptions, but for now we will start with a simple model.

We wrote our computer model in TclTk. You will find it here. The program takes as its input this file containing the names of the layers, their temperatures, and their absorption spectra. It produces the following output.

------------------------------------------------
      Name    Temp       BB     Layer   Escaping
------------------------------------------------
   Surface    290.0    401.1    349.0     89.7
      0-km    280.0    348.5    225.3     58.8
      3-km    270.0    301.3    150.0     49.8
      6-km    250.0    221.5     81.5     44.4
      9-km    230.0    158.7     31.2     15.4
     12-km    220.0    132.8     16.3      5.8
     15-km    220.0    132.8     13.1      4.2
------------------------------------------------
Total:                                   268.2
------------------------------------------------

The "Layer" column is the power radiated upwards by each square meter between 5 μm and 30 μm. The "Escaping" column is the power that escapes. We used 290 K for the surface temperature, which is 17°C. The total power escaping into space is 268 W/m². We don't have radiation from the 18-km layer, because we use this layer only as an absorber for radiation from the 15-km layer. The atmosphere above 15 km plays little or no part in atmospheric convection because it is above the tropopause.

We see immediately that the power escaping from the 15-km layer is only 1.5% of the total escaping power, and twenty times less than the power escaping from the Earth's surface. The top three layers of the atmosphere combined contribute less than 10% to the total escaping power. These are the layers in which radiation is dominated by CO2. In the lower layers, radiation is dominated by water vapor.

Before we proceed with exercising our model, however, we must correct a deficiency in our existing spectra. Our spectra extend from 5 μm to 30 μm, but it turns out that a significant portion of the heat radiated by the Earth's atmospheric layers is radiated in the range 30 μm to 60 μm, as you can see in the graph below. (In case you are interested, we obtained the curves of this graph using this program.)



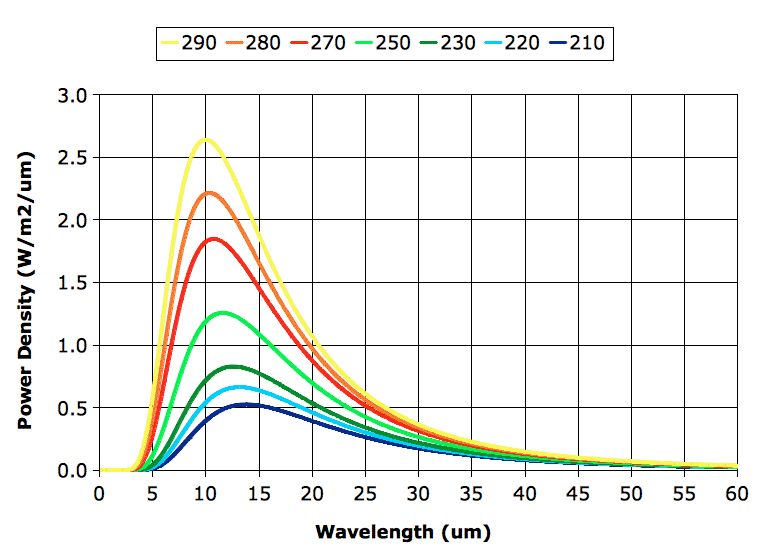
The "BB" column in our table gives the power a black body would radiate, as calculated using Stefan's Law. Our calculation assumes the Earth's surface is a black body, so when we see 401 W/m² in the "BB" column, we expect to see the same value in the "Layer" column. But we don't, and the reason we don't is because our calculation adds up only the power radiated by each layer in the range 5 μm to 30 μm. A black body at 290 K radiates only 349 W/m² in this range. The remaining 52 W/m² it radiates in the range 30 μm to 60 μm.

We must go back to the Spectral Calculator and extend our spectra to 60 μm. While we are there, we will obtain the spectra for 660 ppm CO2 and 165 ppm CO2 as well.