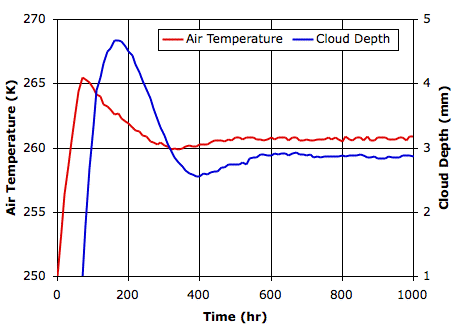
Although our screen shot is taken at thirteen thousand hours, the atmosphere converges to its equilibrium state in a mere eight hundred hours. Our previous simulation converged only after eight thousand hours. The following graph shows surface gas temperature and cloud depth versus time.
The following table compares the equilibrium state of the atmosphere at the end of our two experiments.

The faster-sinking clouds cause the surface to warm by 5.3 K. The Solar power penetrating to the surface increases by 13 W/m2 because the clouds are slightly thinner. You may recall that our current simulation of clouds does not implement their absorption and emission of long-wave radiation, so we are working with transparency fraction set to 0.0, indicating an atmospheric gas that is opaque to long-wave radiation. The only place for this artificial atmosphere to radiate is at the tropopause. So we expect to see the tropopause radiating the same amount of heat that penetrates to the surface: the heat leaving the system must be equal to the heat entering. And indeed this is the case to within a couple of Watts per square meter.
We see that faster-sinking clouds cause the world to warm up, and this is in keeping with our expectation. The icy surface must warm up so that evaporation will keep up with the greater rate of return of water to the surface.
UPDATE: It turns out that our code was allowing clouds to sink only when they took part in a circulation, which resulted in them sinking roughly a hundred times slower than they should have, so our effective sinking rate here was more like 3 mm/s. When we correct our error, so that the clouds really do sink at 300 mm/s, the surface temperature warms by roughly 7 K. [07-JAN-12]

There is something that sounds a little strange. As far as I know an heavy rainfall acts a temperature decrement as it tends to adiabatic saturation value. It seems you obtain a different result. Why?
ReplyDeleteMichele
I'm not sure what you mean by "adiabatic saturation value". There is no rain in my simulation, only the sinking of droplets to the surface. In this case, they are sinking at 300 mm/s, which corresponds to droplets 100 μm in diameter (see graph here). The faster sinking shifts the equilibrium temperature upwards because evaporation can be faster without shutting out the Sun completely.
ReplyDeleteI am used to defining the cooling down produced by the summertime rain as “adiabatic saturation temp” instead of “wet-bulb temperature”. That’s I refer to the temperature that a volume of air would have if cooled adiabatically to saturation at constant pressure by evaporation of water into it, when all needed latent heat is supplied by the volume of air. (http://en.wikipedia.org/wiki/Wet-bulb_temperature).
ReplyDeleteMichele