Condensation Point

Suppose a body of moist air rises from the surface of the sea. The weight of air pressing down upon it decreases as it rises. Its pressure drops. It expands and cools adiabatically (see Adiabatic Balloons). So long as no condensation occurs, its temperature drops by 1°C for each 100 m that it ascends (see Tempearture, Pressure, and Altitude). Will the water vapor eventually condense into droplets?

If we know the initial concentration of water vapor in grams of water per kilogram of air, this concentration will remain constant as the air moves upwards. As the temperature of the air drops, however, perhaps there will come a time when the concentration of water vapor exceeds the saturation concentration, and at that point droplets will form. In Evaporation Rate we presented a graph of saturation concentration versus air temperature. But the data points of this graph correspond to measurements taken on the surface of the Earth, where air pressure is 100 kPa. What will the saturation concentration be at the lower pressures that apply to our rising body of air?

The pressure exerted by a gas is the force exerted by its molecules bouncing off whatever surface they encounter. The pressure of moist air is the sum of the pressures exerted by its nitrogen, oxygen, water, and all other molecules. The pressure exerted by the nitrogen molecules is the partial pressure of nitrogen. The pressure exerted by the water molecules is the partial pressure of water. It turns out that the maximum possible partial pressure of water molecules depends only upon temperature. This maximum is the saturation pressure of water at a particular temperature. Regardless of the other gases that might be mixed with the water vapor, the saturation pressure is always the same at a particular temperature. The graph below gives saturation pressure versus temperature, as indicated by an empirical formula we found here.



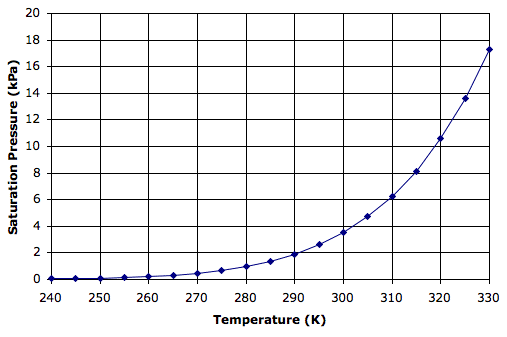
Water vapor is a gas just like nitrogen and oxygen. Its pressure depends only upon its volume and temperature. Water vapor in moist air will be at the same temperature as the air. It will share the same volume as the air. If the air pressure halves, so does the partial pressure of water vapor. For concentrations below a few percent, the concentration of water vapor at various air pressures is given by:

x = p_wR_w/pR = 0.62 p_w/p,

where x is the concentration of water vapor, p_w is its partial pressure, R_w is its specific gas constant, or 462 J/kgK, p is the air pressure, and R is the specific gas constant for air, or 287 J/kgK.

Consider moist air near the surface of the Earth at temperature 300 K, pressure 100 kPa, and water vapor partial pressure 2 kPa, which corresponds to concentration 12 g/kg. The water vapor pressure is roughly half the saturation pressure of 3.8 kPa shown on our graph. Suppose our moist air rises to 2000 m. Its cools to 280 K (1 K per 100 m) and its pressure drops to 80 kPa (adiabatic expansion of air). The concentration of water vapor remains 12 g/kg and its partial pressure drops slightly to 1.6 kPa. At 280 K, however, the saturation pressure has dropped all the way to 1 kPa, which corresponds to a concentration of only 7.6 g/kg. Thus each kilogram of air contains 4.4 g more water than it can hold as water vapor. This excess water must condense to form water droplets.

We would like a simple formula that will allow us to calculate the amount of water that must condense from moist, rising air in our Circulating Cells program. We combine the saturation concentration approximation of our Evaporation Rate post with the specific gas constants of air and water vapor, and with the assumption that the water vapor concentration is small, to arrive at the following approximation.

x_s = (T−250)²p/8000

Here x_s is the saturation concentration of water vapor in g/kg, p is the air pressure in kPa, and T is the temperature of the air in K. At 280 K and 80 kPa, this formula gives us 9 g/kg, which corresponds to a partial pressure of 1.2 kPa. This 1.2 kPa is close enough to the 1.0 kPa shown in the graph above.

The partial pressure of water vapor in moist air decreases as the air rises. But at the same time, the rising air cools by adiabatic expansion, and this cooling depresses the saturation pressure of water vapor so rapidly that condensation will eventually take place. With our approximate formula for saturation concentration with pressure and temperature, we will be able to simulate the condensation of water in moist, rising air.