With Q_heating at 0.01 K, our simulation heats each cell in the bottom row by 0.01 K per iteration. With T_balance at 250 K each cell in the top row cools by 0.01 K per iteration. Our simulation assumes an ideal gas, so the heat required to warm or cool a cell by 0.01 K is always the same. At equilibrium, the heat entering must be equal to the heat leaving. We expect the top row converge to 250 K.
But the top row of CC3 converged to only 240 K. At 240 K, each top cell cools by only 0.0085 K per iteration. With circulation turned off, however, and only mixing to transport heat, the top row of CC3 did converge to exactly 250 K. We concluded that something was amiss with our circulation routine: it was making heat disappear.
In Work by Convection we showed how the expansion of warm, rising air does more work than is required to compress cool, falling air. The excess work manifests itself immediately as an upward force on the rising air. We could harness this force with a wind turbine. Otherwise the rising air will accelerate into a turbulent flow. Over time, viscous friction will transform this kinetic energy into heat. We discussed this phenomenon in Dissipation by Convection, and concluded that work by convection is what powers storms and winds.
Suppose we have a block of four cells in our simulation, at the bottom of the cell array. The lower-left cell is at 320 K while the upper-right is at 300 K. We rotate the block clockwise. The lower-left cell rises. Its pressure drops by 3.3 kPa, this being the weight per square meter of a single cell in CC3. If the cell expands adiabatically, its final temperature will be 320 K × 0.9903 = 316.90 K. Meanwhile, the upper-right cell falls. Its pressure rises by 3.3 kPa. Its final temperature will be 300 K ÷ 0.9903 = 302.94 K. One cell cooled by 3.10 K while the other warmed by 2.94 K. The two remaining cells, which do not change pressure, neither warm nor cool.
Both cells have the same mass, and the ideal gas inside has constant specific heat capacity Cp = 1.003 kJ/kg. One cell lost 3.10 kJ/kg while the other gained 2.94 kJ/kg. The difference is 160 J/kg. This 160 J/kg is the work done by the circulation. We did not account for this work in CC3. Each time a block rotated, the work by circulation disappeared.
Our CC4 program provides several new features. You can save the array temperatures to a text file, and load them also. You can track the movements and temperature of marked cells with the Tracking option. Within the code, we have greatly expanded the explanatory comments and we have simplified some of the routines and global variables to make future enhancements easier. But most important, CC4 accounts for the work done by circulation, as you can see for yourself in the circulate routine. The Viscosity option indicates whether or not we account for the dissipation of work by viscosity.
When CC4 rotates four cells, it calculate the work available just as we did above. We assume this work goes into accelerating the air within the cells and ends up dissipating as viscous friction within the four cells. The simulation adds the viscous heat to the four cells equally. The following graph shows the temperature profiles we obtained from CC4 after a million iterations for various values of mixing fraction (M) and heating rate (Q). Click on the graph for better resolution.
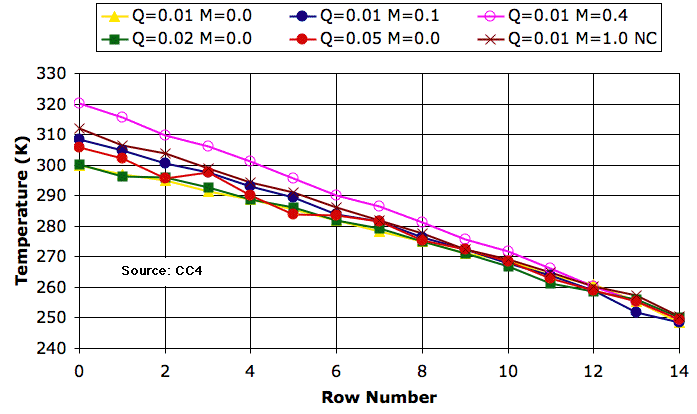
The top row converges to 250 K in each case. With no mixing, the bottom row is 50-K warmer than the top. With mixing fraction 0.1, the bottom is 58 K warmer than the top. With mixing fraction 0.4, it is 70 K warmer. The effect of mixing is almost exactly the same as it was for CC3. Also in the graph, you can see the profile that results when we turn off the circulation (NC) but set mixing fraction to 1.0. Heat is transported by mixing alone and the bottom is 62 K warmer than the top.
We conclude that the incorrect convergence of CC3 was indeed the result of our ignoring work by circulation. Indeed, we can obtain the CC3 results with CC4 simply by turning off CC4's viscous friction adjustment.

Kevan,
ReplyDeleteif you want we can refer to the works but we need to take into account all the done ones. As the rising/falling cell isn’t at rest we must operate with the fluid/gas dynamics.
The momentum equation in the steady state for the unidirectional and inviscid case tell us
ρu • δu/δz = - ρg - δp/δz = - ρ(g + RδT/δz)
Thus, the cell is pushed upward if δT/δz > - g/R and downward if δT/δz < - g/R. Anyhow the motion and its sense is only affected by the vertical temperature gradient . The climatic experts say that the atmosphere becomes convective upward when is δT/δz < - g/Cp and that strongly contradicts the momentum equation of gas dynamics. How is it possible?
The cell at 320 K is the most energized of the group and, rising, executes the work needed to push down the cell at 300 K.
Both the gravity force and the pressure gradient operate and the total mechanical work done by the external forces on the cell is the sum of the gravitational one ΔWg = - ρgΔz and of the thermodynamic work of displacement ΔWth1 = - ρRΔT. So the total work done by the cell is ΔW1 = - ρgΔz1 - ρRΔT1 . The total work is used in pushing down the cell at 300 K that’s ΔW2 = ρgΔz2 - ρRΔT2.
The group of four cells doesn’t exchange work with the surrounding, then it must be ΔW1 + ΔW2 = 0 and so, being Δz2 = - Δz1, will be also ΔT2 = - ΔT1.
The energy equation states in general for the inviscid fluid in steady state, taking into account only the convective terms, that (CpT + u²/2 + gz) must be constant, as already said before. So it is again abs(ΔT2)=abs(ΔT1)=gΔz/Cp
All that without the viscosity that can be introduced taking into accont its influences into the momentum and enerigy equations of gasdynamics.
In your computing is missing the work done by/on the pressure gradient and gravity. That causes the differences between the two ΔT.
Michele
Dear Michele,
ReplyDeleteI'm looking at your < with −g/Cp and I think you may have one of them the wrong way round. Anyway, heat escapes from the Earth's atmosphere at all altitudes. Perhaps the escaping power allows convection for dT/dz > −g/Cp (that is, a slower drop in temperature with altitude). We'll see in later versions of the simulation.
In your work done by each cell, I think you should have ΔW2 = −ρgΔz2 − ρRΔT2 (gravity term has a minus sign too). Also, I'm assuming that ρ is the mass per cell. In that case we get:
−ρgΔz1 − ρRΔT1 −ρgΔz2 − ρRΔT2 = 0
When we decide whether or not to rotate cells in CC4, we do not assume that Δz2 = - Δz1. We account for the fact that the center of mass of Cell 2 will be slightly lower than the initial height of Cell 1, because Cell 2 is colder. Furthermore, there is another cell that changes altitude: the one that slides from on top of Cell 1 to be on top of Cell 2. We assume that the fourth cell slides sideways on a base that is horizontal, but we know even this is not true, because there is heating and circulation in the rows below.
But even more important: the altitude of cells outside our block of four will change when we circulate. We do not take account of these movements outside when we circulate inside.
When our simulation converges, however, the altitude of the rows remains constant on average. Thus we know that the sum of all the Δz terms for all the cells, accounting for those inside and outside, will be zero on average. So we can ignore the Δz terms and the effect upon our convergence will be exactly zero.
That is what we do in the simulation: we ignore work done raising and lowering the centers of mass.
When we calculate the temperature change due to adiabatic expansion we assume a certain change in pressure, which is accurate because our cells are of fixed weight. We assume uniform pressure through the cell, which is not realistic, but that's the basis of our simulation: uniform temperature and pressure within each cell.
You seem to be ignoring the momentum of the cells because you say their energy is only gravitational and thermodynamic. Suppose the four cells were at rest to begin with, and all get to the same velocity u at the end of the movement.
−RΔ(T1+T2+T3+T4) = 2u^2 + Δ(z1+z2+z3+z4)
We set the z terms to zero for the reasons given above. They add up to zero when we include the effect of circulation upon cells outside our block of four.
But we cannot ignore the kinetic energy term, which is always positive. My claim is that this kinetic energy will be dissipated as viscous heat within the block of cells. So we divide it by four and put it back into the cells equally.
Yours, Kevan
Kevan,
ReplyDeleteYou are right, I quarreled with the signs.
“ δT/δz < - g/Cp”
This is not a my sign, it belongs to literature.
You can see here (http://www.forestencyclopedia.net/p/p426), but it is possible to search more and more others, where is stated that:
1) the atmosphere is instable with a lapse rate superadiabatic δT/δz < - g/Cp
2) the atmosphere is neutral with a lapse rate adiabatic δT/δz = - g/Cp
3) the atmosphere is stable with a lapse rate hypoadiabatic δT/δz > - g/Cp
Analyzing the momentum equation we obtain that:
1) the atmosphere is autoupwelling (read autoconvective) with a lapse rate δT/δz < - g/R
2) the atmosphere is at rest with a lapse rate δT/δz = - g/R
3) the atmosphere is autodownwelling with a lapse rate δT/δz > - g/R
Question:
The effective lapse rate is near adiabatic, the resultant of forces on the cell - ρ(g + RδT/δz) acts downward, then what is the engine of the convection?
I think that the circulating simplifies if computed as the torque of the acting forces which operates with the same lever arm respect to the center of the four cells. The total torque of gravity is zero and so the cw torque on the group would be proportional to (T10 - T00) - (T11 – T01), assuming that is negligible the difference of the distance between the center of mass of the two cells of the same column. The error will vanish iterating.
I am thinking statically, assuming that the motion, when occurs, is very slow so that we can neglect the KE and the viscosity.
Of course it is possible to improve the picture of the process using together all the gas dynamics equations, increasing the complexity of the speech. That’s takes more time.
Michele
Dear Michele,
ReplyDeleteThank you for your continued collaboration on this subject. Your latest comment ended up in the SPAM box again. With any luck, the SPAM filter will learn not to do that. But at least I understand the problem now.
I don't want to guess at why the climate science literature has it wrong. But I agree that they have it wrong.
I like your terminology: "superadiabatic" means δT/δz < - g/Cp. The temperature drop from surface to tropopause is greater.. And "hypoadiabatic" for a lesser temperature drop. So far as I know, the Earth's atmosphere is hypoadiabatic.
Without mixing, I agree that the atmosphere is unstable when superadiabatic. But mixing makes the laps rate superadiabatic, as we have seen.
You ask what is the engine of convection when the laps rate is hypoadiabatic? If I could answer that question with confidence, I would not be building a simulation. My intuition has been wrong so far. I thought mixing would decrease the gradient. It did the opposite.
Nevertheless, here is my answer, based upon intuition. Atmospheric convection is not a steady circulation. It is a chaotic combination of many small circulations. If you remove heat from all rows, you will see that a cell in row 3 will cool until it falls. It cannot remain in row 3 forever. The variation in temperature along the rows will increase until there are some cells cold enough to fall, even though the average laps rate is hypoadiabatic.
That's my guess. I'm hoping the simulation will show us.
I continue to disagree with you about the KE and viscosity. The KE imparted to the cells is the source of convection. Without the KE, there would be no convection and no adiabatic laps rate. Heat would have to travel by mixing and radiation alone. There would be no storms and no tornadoes. So if we ignore this term, however small, we are ignoring from the beginning the force that drives some of the most interesting phenomena we want to investigate.
Furthermore, if you say that the temperature change for gas at 320 K going from 103.3 kPa to 100 kPa is the same magnitude as for gas at 300 K going from 100 kPa to 103.3 kPa, we know that is wrong. There is a small difference, and this difference accumulates as cells rise up, until 15% of the incoming energy disappears. I think 15% is significant.
I want our simulation to identify and deal with the work by circulation. In future versions of the code, we may try to remember the momentum of individual cells, which may lead to larger circulations beyond a single block. In that case, we will need to know how the momentum is affected by each circulation. It is the work available from convection that tells us how much momentum can be imparted.
You say the motion is slow. Well, let's take a look at that. On average, T1+T2 decreases by 0.06 K in a circulation. The rising cell has cooled by 0.06 K more than the falling cell has warmed. Thus we have 0.06 * Cp = 60 J/kg available for KE, and we must multiply by the mass of the first cell. We distribute this 60 J/kg among the four cells, so each kilogram of gas receives 15 J. The cells begin to move at 5 m/s.
That's not insignificant. After ten such circulations, if you ignore the KE, the cells are moving at 50 m/s. Pretty soon they will be supersonic, because they don't slow down even when they reach the tropopause. Only viscosity slows them down.
Yours, Kevan
CORRECTION: After ten circulations they will be moving at 15 m/s. It will take around 4000 circulations to reach supersonic speed. Kevan
ReplyDeleteJust a point about the viscosity.
ReplyDeleteIf we was analyzing some experimental data all the hypothesis are allowable as we don’t know what could affect the results. In a numerical simulation the output must be coherent with the input: no viscosity input, no viscosity output. I think it is a fundamental principle for a correct methodology.
I insist on my idea about the ΔT. The rising cell uses its thermodynamic energy for to execute the adiabatic expansion work (CvΔT) and the work against the gradient of pressure (RΔT) obtaining the increase (gΔz)of its mechanical energy and because the energy conservation must be CvΔT + RΔT + gΔz = 0 for any displacement of the cell.
I suggest another test for the global test of the simulation.
Setting T_bottom = 100 bar and T_top = 0.25 bar we would obtain anything analogous to the Venus’ atmosphere, i.e. a ΔT = 500 – 600 K. It seems to me that the convergence is different. It is needed a long time. I start now the compute and I will see a few hours later what will occurs.
Michele
I have set p_bottom = 100 bar, p_top = 0.25 bar, Q_heating = 0.06, row number = 31. About five hours later there isn’t convergence but T_bottom – T_top varies between 500 and 540 K, T_mean (16th row) between 235 and 255 K. In practice the Venus’ parameters.
ReplyDeleteIndeed, we have the following conditions:
adiabatic atmosphere T_b – T_t = T_b*(1 – (p_t/p_b)^R/Cp) = T_b*f(p)
adiabatic lapse rate T_b – T_t = gH/Cp
convective flux T_b – T_t = Q_c/h = x*Q_tot /h
radiative balance at the top T_t = (x*Q_tot/σ) ¼
where H is the troposphere height, h is the convective coefficient, x is the % of total flux emitted by the tropopause.
So, the problem in well known. The condition of adiabatic atmosphere , i.e. f(p), seems not to affect the equilibrium thermodynamic and radiative of the atmosphere. But I think that the pressure does to affect the parameter x %.
Michele
Dear Michele,
ReplyDeleteI can see the value of your principle of simulation. But I think it is contradicted by the example I gave with the propellor in a box. The box's walls are rigid. The bearings have no friction. I turn the propellor. The gas in the box offers resistance. I do a certain amount of work turning the propellor. If the gas is very viscous, the propellor will turn more slowly. If it is hardly viscous at all, the propellor will turn more quickly. Either way, by assumption, the amount of work I do is the same, and this work turns into heat in the gas.
In other words: I don't need to know the viscosity of the gas to tell you how much it warms up. The same thing happens in our circulation of cells. I know there is excess work and that this work accelerates the cells. If I assume the cells remain within the rigid boundaries of the block of four cells, and I assume that time enough elapses that they come to a stop, their energy must be dissipated as viscous heat, regardless of the viscosity.
Of course, the viscosity cannot be zero, but the viscosity of air is very far from zero. If you turn off a fan in a closed room, it takes less than a minute for the air to come to a stop. It comes to a stop because of viscosity.
Your calculation of work done increasing gravitational potential is incomplete: you must add the work done raising all the cells above the block of four. Furthermore, you cannot assume that the bottom of the block of four cells is flat, because cells below have been raised and lowered. We could account for all the gravitational changes, by giving each cell a precise height. But I believe I showed that in the end this added complexity would come to zero because the average altitude of the rows is not changing at convergence.
Of course, if the program does not converge, we will have to consider the different altitudes of cells in the same row.
Yours, Kevan
Dear Michele,
ReplyDeleteI revisited my post on Venus. I see that I used the ideal diatomic gas equation to calculate the surface pressure. But most of the atmosphere of that planet is CO2, for which the ratio Cp/Cv is smaller because of its larger number of degrees of freedom. Consequently, the adiabatic compression equation is closer to p^−0.25.T^1.25. Thus our simulation, using the diatomic gas equation won't be accurate. But I see that it comes up with roughly the correct result anyway.
Yours, Kevan
I wanted simply to see what could occurs if the Heart’s p_bottom was 100 bar. It seems that we had analogous condition than Venus only taking account of convection.
ReplyDeleteMichele
Dear Michele,
ReplyDeleteYes: I like your experiment very much. I did not comment upon it further because I wanted to try it myself. I see that you increased the number of cells vertically to account for the greater pressure drop. We have been using 15 rows for a factor of two change in pressure. On venus, the factor is closer to 1000, which is 10 factors of 2, so we may need 150 rows to give a good result. I thought I would try 150 rows, but decrease the size of them on the screen. It may be that the convergence is better with more rows.
Also: I tried to look up "Heart's Pressure" before, but could find nothing about it. Can you explain to me?
Yours, Kevan
I agree with you. The convergence will get better increasing the row number, but reading the string of reporting data will be impossible. I think that would be better in this case to send at the screen only the values of the rows 1 (T_bottom), (jmax+1)/2 (T at pmean) and jmax (p_top) that are the most interesting.
ReplyDelete"Heart's Pressure"
I don’t understand you question. Would you reformulate it?
Michele
Dear Michele,
ReplyDeleteGood point about the results line. I'll work on that now.
You said, " if the Heart’s p_bottom was 100 bar." And I wanted to know what "Heart's" meant.
Yours, Kevan
Some time ago I read on line
ReplyDeletehttp://scienceofdoom.com/2010/08/16/convection-venus-thought-experiments-and-tall-rooms-full-of-gas/
http://arthur.shumwaysmith.com/life/content/the_arrogance_of_physicists
http://moyhu.blogspot.com/2010/06/venus-models-and-adiabatic-pump.html
animate debates about the causes of the very high Venus’ ground temperature.
Somebody argued about what could be occur if the Heart’s atmosphere had a mass 100X the actual one, i.e. if the Heart’s p_bottom was 100 bar.
I was just asking you simulation out of curiosity.
Michele
Dear Michele,
ReplyDeleteI'm still not sure what "Heart" is. Are you referring to the organ in the body that pumps blood? Is "Heart" the surname of a scientist?
Our simulation does not work well with the 10 kPa to 9,300 kPa pressure differential of Venus. Each cell in our array represents the same mass of gas. If I divide into 120 cells, we get each cell representing a pressure drop of 77 kPa. The top cell spans the range 77 kPa to 10 kPa, which is a factor of 7 in pressure. With T_balance = 240 K, I see row 0 settle to 670 K, row 110 settle to 439 K, and row 119 settle to 250 K. We get 200 K drop in the final 9 rows. Furthermore, the effective radiating temperature of the top row is 260 K, which is 20 K too high.
Yours, Kevan
Gosh, my language issues are more serious than I thought. Indeed I would refer to planet Earth. Thanks for the way of making me understood about my mistake. It will come in useful in the following.
ReplyDeleteI also tried with 121 rows and the temperatures trended to diverge whereas they converged with 31 rows. From what this could depend on?
If we consider Q_heating is the heat flux wasted at the top of the column when T_top = T_initial, then a lower T_balance requires a lower heat flux Q_h1 = Q_heating*(T_balance/T_initial)^4 that has to be the same at the bottom and the top for a correct convergence of the simulation. Surely that will be useful for the eventual balance of the heat fluxes.
Michele
Dear Michele,
ReplyDeleteI see: Heart = Earth. I should have guessed. Thank you again for making the effort to speak English.
My simulation with 120 rows and Q_heating 0.01 converged. Were you using a larger value of Q_heating? If so, the variation in temperature between cells in the same row starts to get large compared to their absolute temperature. The average row temperature fluctuates by 100 K or even 200 K. But the simulation never "diverges" in the true sense of the word: the temperature does not rise to infinity or sink to zero.
I don't understand why we would consider Q_heating to be the "heat flux wasted at the top of the column when T_top = T_initial." I think you see a relationship between thermodynamic equilibrium and gravitational equilibrium that I don't see, so I don't understand your argument.
Yours, Kevan