In a debate that took place in the comments, one of our readers claimed that a temperature difference must always exist between the bottom and the top of an atmosphere. Air is always circulating to some degree, he said, and any air that rises must cool adiabatically. He asserted that the temperature as we ascend through the atmosphere will be related to the pressure by the equation of adiabatic expansion. In Adiabatic Magic, however, we showed that our reader's claim violated the Second Law of Thermodynamics. Spontaneous adiabatic circulation of air in the atmosphere is impossible.
If spontaneous, adiabatic circulation is impossible, there must be some physical process that stops it from happening. Although we have proved that some such process must exist, we have not yet described the process. We will attempt to do so today.
Consider the following diagram. We have a column of air 5 km high, enclosed in a box. The temperature of the air is uniformly equal to 250 K. Because of the weight of the air, the pressure at the bottom is twice the pressure at the top. We have a balloon of air at the top, and another at the bottom. Each balloon is insulating and reflecting, so no heat passes in or out. Each balloon is flexible, so the pressure of the gas inside is always equal to the pressure outside.
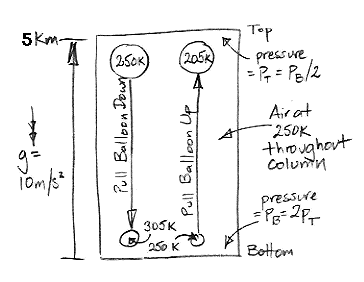
We attach a string to the upper balloon and start to pull it down. As it descends, the air around it pushes in upon it with greater pressure so as to compress its volume. The air inside undergoes adiabatic compression. Its pressure, p, and temperature, T, are such that the product p 0.4T −1.4 remains constant.
We pull the balloon all the way down to the bottom of the column. Its pressure has doubled, so its temperature must rise from 250 K to 305 K. Our balloon has grown smaller, so the surrounding atmosphere must have expanded, and therefore cooled. But suppose our column is enormous compared to the balloon, so the cooling of the air outside the balloon is negligible. The air inside is at 305 K, and that outside remains at 250 K. The density of the air outside is 305/250 = 1.2 times greater than that of the air inside. Every kilogram of air in the balloon occupies the same volume as 1.2 kg of air outside the balloon.
By the principal of buoyancy, every kilogram of air in the balloon will experience an upward force equal to the weight of 0.2 kg of air. If we assume gravity is 10 m/s/s, we see that we must hold the balloon down with a force equal to 2 N/kg (two Newton per kilogram of air inside) or else it will rise, and it won't stop until it gets to the top again.
This buoyancy force was zero when we started pulling the balloon down, and at the end it was 2 N/kg. The average force would be close to 1 N/kg, which we apply over 5 km, so we must do roughly 5 kJ/kg of work to pull the balloon down.
Now suppose we pull the lower balloon up from the bottom at the same time. The net change in the volume of the rest of the column is is now zero, so we really can say that the outside air remains at 250 K. This other balloon, when it reaches the top of the column, will have expanded. It's pressure has halved, so its temperature must drop from 250 K to 205 K. It's density is 1.2 times greater than the air around it, so it will experience a negative buoyancy force of 2 N/kg. If we don't pull it up, it will sink all the way to the bottom again. In drawing it up, we must do 5 kJ/kg of work.
We must do 5 kJ of work to raise a single kilogram of air from the bottom to the top, and 5 kJ to lower another kilogram from the top to the bottom. Thus we see that the spontaneous circulation of air suggested by the Adiabatic Magic hypothesis is indeed impossible. It is buoyancy that stops the magic. We need a source of work to cause circulation, and no such source exists in our column of air at a uniform temperature.
One source of the necessary work is a heat engine in which we supply heat at a higher temperature to the bottom of the column and extract heat at a lower temperature from the top. Any time we have a source of heat at a higher temperature, and a place for the heat to flow to at a lower temperature, we can make a machine that does work. In the atmosphere, this machine is implemented, albeit inefficiently, by convection. We discussed work by convection earlier, but we we will return to it in future posts.
UPDATE: I originally made the column 10 km high, but Michele pointed out that I had my math wrong. The column should be 5 km high. Indeed, it turns out that the heigh of the column for which we have half the pressure at the top is a function of temperature only, which did not occur to me until I tried to duplicate Michele's calculation. See comments for details.

Kevan,
ReplyDeleteAllow me to point that in an isothermal column 10 km high and at 250K the pressure at bottom is nearly four times than at top. But this doesn’t affect what you say in the rest of your post.
I think your isothermal condition isn’t necessary as the works of weight and buoyancy to raise a single kilogram of air from the bottom to the top and to lower the same or another kilogram from the top to the bottom are always identical because the gravitational field is conservative. That’s however evolves its temperature.
Michele
Dear Michele,
ReplyDeleteI was mistaken. The pressure ratio is constrained by the temperature, in exactly the way you suggest. Let me do the math here for the benefit of other readers.
Referring back to Atmospheric Pressure, our constant f = p/ρ is of course equal to RT, where R is the gas specific gas constant for air, and is 287 J/kgK. Our equation for pressure with height becomes p = p_B exp(−gy/RT). (Note that "exp" is "e to the power of" because I can't do superscripts in these comments).
Pressure drops by 50% when −gy/RT = −0.7, which means the height at which the pressure has dropped by 50% must be −0.7RT/g. If we choose T = 250 K, we get half the pressure at an altitude of 5 km, and as you say: one quarter the pressure at 10 km.
This result holds regardless of how much air we push into my sealed column. The more air we push in, the greater the density of the air, and the more rapidly the pressure drops as we ascend, so the ratio of the top and bottom pressure remains the same.
If we want the top pressure to be half the bottom pressure, we have to set the gas at twice the temperature: 500 K.
So, thank you for pointing out my mistake. I will update the post to warn future readers.
Yours, Kevan
Kevan,
ReplyDeleteThinking back over the matter, the works needed to bring the same balloon from the bottom to top and then to get back it to bottom are identical; but the works needed for the two balloons (rising and sinking) are different.
The force acting on the balloon is F = gV(de-di) = gVdi(de/di-1) = gVdi(Ti/Te-1) and the one acting on unity of mass of air contained by the balloon is F* = g(Ti/Te-1).
For the rising balloon and isothermal atmosphere, you have outside of balloon p/pb = de/db = exp(-gz/RT) and inside Ti/Te = Ti/Tb = (p/pb)^1/k = exp(-gz/cpT).
In the case of sinking balloon is p/pt = de/dt = exp(g(H-z)/RTe) and Ti/Te = exp(g(H-z)/cpT).
The above symbols are: g gravitational acceleration (10 m/s2), V bolloon volume, d density, i internal, e external, b bottom, t top, T temperature (Te=250K), p pressure, z altitude, H column height (10000 m), R = cp-cv gas constant, cp heat capacity of air (1000 J/kg).
The rising work is the definite integral of g(exp(-gz/cpT)-1) over 0 to H, equal to -17580 m2/s2, and the sinking work is that of g(exp(g(H-z)/cpT)-1) over H to 0, equal to -22960 m2/s2.
Of course, unless I have not been wrong in some point.
Michele
Dear Michele,
ReplyDeleteI'm at CERN right now, 100 m below the ground, working on some electronics. But I could not resist checking your integrals. I am delighted with the form you arrived at: so elegant to have the force per kilogram equal to g(Ti/Te - 1). That's beautiful.
When I integrate over 10 km for the upward balloon I get 17580 J/kg just as you do. Over 5 km I get 4680 J/kg, which is close to my estimate of 5 kJ. For the upward balloon I get the same result, when integrating your equation. In fact, substituting y = (H-z) we see the integrals must be the same, because the limits for y become 0 to H.
I will say that I had to do the integral sums over and over again in my notebook because I kept getting them mixed up. So I may be mistaken. But please check for me.
Yours, Kevan
Kevan,
ReplyDeleteIt is necessary to set attention to the fact that the argument of the exponential is negative for the upward balloon and positive for that downward.
So the definite integrals would be for the first case
W* = – cpT(exp(-gH/cpT) – 1) – gH
and for the second case
W* = – cpT(exp(gH/cpT) – 1) +gH
They are effectively different.
Michele
Dear Michele,
ReplyDeleteI now get the same answer as you: 22,500 J/kg for pulling the balloon down by 10 km. For 5 km I get 5.3 kJ/kg to pull it down, and 4.7 kJ/kg to pull it up.
The difference now makes sense to me. On the way down, the biggest difference in temperature occurs when the density is highest, thus increasing the lift. On the way up, the biggest difference in temperature occurs when the density is least.
I like the way you arranged the equations: you get rid the 0.4, 1.4, and 2/7 fractions by referring back to Cp, Cv, and R. I will try to do that from now on.
Yours, Kevan
Kevan,
ReplyDeleteYou arrive more quickly to the same result thinking in energetic terms.
Upward.
Eb = CpT; Et = CpTexp(-gH/CpT) + gH; W* = Et – Eb = CpT(exp gH/CpT) – 1) + gH
Downward.
Et = CpT + gH; Eb = CpTexp(gH/CpT); W* = Eb – Et = CpT(exp(gH/CpT) – 1) – gH
Michele
Dear Michele, That's lovely. In general, I try to steer away from using the Energy Short-Cut in my calculations. In my experience, non-scientists get confused about energy. Many people seem to think that energy is something that exists as a substance or a field or something, so they have Creatures of Pure Energy in Star Trek. Having said that, I fully appreciate that your second derivation is complete and elegant, and I admit that it did not occur to me until you pointed it out. Yours, Kevan
ReplyDelete