During the day, most of the heat passing into the surface gas cells does so by convection. But convection occurs only when the gas above is cooler than the surface below. In our discussion of atmospheric inversion we saw how the ground can be colder than the surface air at night, which can lead to a pocket of cold air sitting near the ground, with warmer air up above. In our simulation, we set the convection transfer to zero when the surface is colder than the surface gas.
At night, therefore, a sandy surface will radiate its heat into space, and receive no warmth from the sun. But it will receive warmth from the atmosphere, in the form of the back-radiation we described in our previous post. During the day, we found that our surface gas was radiating 226 W/m2 down to the surface. This radiation will slow the cooling of the surface at night.
We ran our simulation with Cycle heating on a sandy planet surface, 700 W/m2 solar heat during the day, daylight fraction set to 0.50, convection coefficient 20 W/m2, and transparency fraction 0.50. You will find the equilibrium state of the cell array at midnight stored in a text file here. The following graph shows the average temperature of the sand blocks, the surface gas cells, and the tropopause gas cells during two complete day-night cycles. We plot the deviation of each temperature from its average value during the cycles, which is why we call the plots "anomalies".
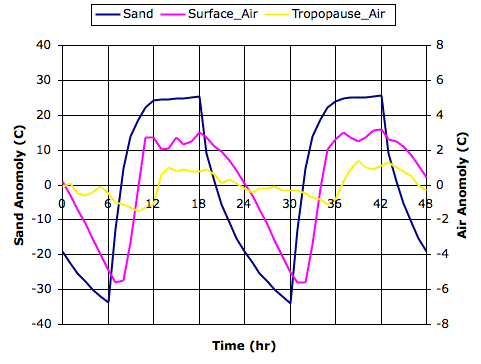
The temperature of the surface sand varies by almost 50°C, dropping as low as −12°C just before dawn. The temperature of the air a hundred meters above the sand, at the center of the bottom row of gas cells, varies by 9°C, dropping as low as 23°C. The tropopause responds far less to the day-nigh cycle, with a variation of only 2°C. These results are consistent with our observations of the desert, which we discussed at length in our Surface Cooling posts.
When we turn off the back-radiation in our simulation, the temperature of the surface sand drops by another 50°C at night, in a manner reminiscent of the Moon. And so we conclude that our atmosphere, by means of back-radiation, keeps us warm at night.

Hi Kevan, a long time has passed, I hope that you are well.
ReplyDeleteI have something to object about your relationship
“Emitted Tropopause Radiation = σ(1-τ)(TT)4”
(by the way, how do you get the superscripts and the subscripts, as the tags ”sup” and ”sub” don't work?)
You correctly affirm that the troposphere is convective and that, therefore, the tropopause is the sink for the whole heat that is not expelled in the space by the surface radiation. Then the tropopause is the region of the atmosphere where the arriving heat is converted to radiation by the CO2 and then it is disposed of to space.
Viewing the Earth’s and Venus’ temperature profiles ”(see here for example)” we read that both the planets have a convective layer above the surface where the atmospheric gases rise by buoyancy.
The spectra of brightness temperature ”(see here for example)” point up that the minimal values of the temperatures, which occur at the top of the convective layers having their bottom closer to ground, are due to CO2 and they coincide with the real temperatures. (By the way, notice that Earth without oxygen would be Venus-like also if its pressure is circa one hundredth).
Then I think that the emitted tropopause radiation is not only affected by the troposphere absorption because the sensible and latent heat exchanged at the surface (a not negligible amount) wouldn’t be taken into account and so the emitted tropopause radiation is the sole CO2 bandwidth around the 15 microns at the tropopause temperature (the about 15 W/m² that you obtained). That’s, all the energies wasted to heat within the atmosphere are collected into the tropopause by the convection (which sweeps the whole troposphere) and then they are converted and disposed of. In other words the CO2 cools, it doesn’t warm.
I diffusely argued on the matter with Patric027 at
http://skepticalscience.com/news.php?p=1&t=54&&n=803
I would know your opinion about it.
Michele
Dear Michele,
ReplyDeleteWelcome back, and thank you for your interesting question. Indeed, it is true that increasing the carbon dioxide content of the atmosphere increases the efficiency with which the tropopause will radiate heat into space. And we see this in the Total Escaping Power values that we calculated in With 660 ppm CO2.
Our Total Escaping Power calculation used the spectra of gases at realistic concentrations in six layers of the atmosphere, so that each higher layer was thinner than the last, and allows radiation from lower layers to pass through to space.
There are two effects, therefore, when we double the CO2 concentration. One is the effect you describe, where the upper layers of the atmosphere radiate more. According to our calculations, the atmosphere from 9 km to 18 km altitude radiate 0.8 W/m2 more into space. The other effect is to increase the absorbing power of the lower layers, so that the surface of the Earth radiates less heat directly into space. We calculated that 7.2 W/m2 less heat would escape from the surface and the first 9 km of the atmosphere.
The surface alone will radiate 1.6 W/m2 less, but it's the lowest layer of the atmosphere that sees the greatest decrease in escaping power: 3.3 W/m2 less.
Thus my answer is: you are right that the increased CO2 causes the tropopause to radiate more power at the same temperature, but this effect is outweighed by the decrease in heat escaping directly from the surface.
I looked a the skeptical science link you sent me. Here's what one guy said to you, "you are using imprecise concepts, or at least imprecise language, which may lead you to confusion." He then goes on to quote formulas and make imprecise arguments, but fails to do any calculations.
Yours, Kevan
Are you sure that the Kirchoff law is applicable to a gas in convective motion which experiences a continuous change of its temperature?
ReplyDeleteThe required LTE doesn’t exist and Kirchoff is unlikely to hold.
What is and/or becomes heat within the convective troposphere remains heat and it is transferred by convection until the isothermal tropopause where the LTE is now possible and then the heat can be converted to radiation by the CO2 and so disposed of. Otherwise the sensible and latent heat yielded to the atmosphere by the surface couldn’t be eliminated as it doesn’t take place in the process of emission – absorption – reemission and so on of the radiative transfer. I think that, perhaps, your balance at the tropopause has to be reviewed.
Michele
Dear Michele,
ReplyDeleteYes, I'm quite certain that Kirchoff's Law applies, regardless of movement or changes in temperature. It applies to any material at any moment in time. If it did not, then you could create a machine that violated the second law of thermodynamics. In our radiative symmetry post, we describe Kirchoff's thought experiment, with some gas and a black body inside a box with reflecting walls. It does not matter how much you stir the gas, nor how much heat you deliver to it or take away from it. The exchange of radiation between the black body and the gas is still constrained in the same way. Furthermore, the same radiative symmetry comes out of the quantum-mechanical description of black-body radiation. It applies instantaneously to any atom or substance, regardless of its temperature or movement.
What is LTE?
So, you can see that I remain confident in our radiation calculations, all of which are founded upon the principle of radiative symmetry.
Yours, Kevan
LTE is Local Thermodynamic Equilibrium and it is ‘condicio sine qua non’ because the Kirchoff law is applicable.
ReplyDeleteLTE means constant temperature and constant other thermodynamic properties of the gas and overall constant radiative temperature within all the 4π steradiants around it, as it is assured for the gas contained inside the cavity.
Sorry, I will be absent for some time.
Michele
I have just reentered from vacation and I take back my talk from the point where I had interrupted it.
ReplyDeleteViewing this slide of Venus emission spectra from different latitudes "Figure 1" you can see that the brightness temperature is in the range of 230-260 K excluding the bandwidth centered on 667 cm-1.
Also, viewing this other slide of Earth emission spectra from different latitudes "Figure 2" you can see that the radiance strongly changes unless at 667 cm-1 where it remains constant, about 4 (W/cm²sr)cm.
That’s, the TOA (TopOfAtmosphere) radiation is generally affected by the surface temperature and the Venus’s/Earth’s atmospheres behave as a Gray Body for all the spectral frequencies except that for the CO2 vibrational frequency of 667 cm-1 where the two atmospheres behave as a Black Body which:
- is never passed trough by the radiation
- transfers within it the energy only as heat
- converts the heat to radiation within its skin (where the conduction/convection are no longer effective)
- disposes off it to space.
So, I think that the atmosphere:
- sells of all the wasted energies (that otherwise it would accumulate into it) using the small windows centered on the 15 micron wavelength, i.e., using the CO2, which really cools the atmosphere
- makes up also an impedance for the surface radiation (which is a variable property as the alternate current (the Poynting vector is a complex property)) and thus allows that only its active component escapes to space, whereas its reactive component is continuously exchanged between the surface and the atmosphere without a useful effect.
The parallel radiation – AC holds well. If the reactive component arises we have to increase the forcing (temperature – voltage) if we want continue to obtain the same active component (useful effect), otherwise the active effect tends to vanish.
I think that the exact energy balance at TOA must have two addends:
- sigmaTTOA^4*CO2band% that equals the heat convected to the tropopause by the troposphere
- signaTs^4*(tau)*(1- CO2band%) where, in effect, (tau) is the power factor of the radiation transfer trough the atmosphere.
Michele
How do you deduce the Top of the Atmosphere radiation from your graphs?
ReplyDeleteThe Earth graph shows radiation directly from the planet surface, with drops in power for CO2 and water vapor absorption. It was recorded on clear days. You will find the absorption spectra of the Earth's various atmospheric layers in our Earth's Atmosphere post.
The Venus graph shows something called "emission temperature", which assumes the radiation at each wavelength is emitted by a black body, an assumption that is incorrect, as you have pointed out. Better would be to plot the power emitted, as in your Earth graph.
In any event, the CO2 emission temperature is so low because the atmosphere becomes transparent in at 15 μm (667 cm-1) at a far higher altitude than it becomes transparent for other wavelengths.
So I guess I still don't understand your point. There is nothing in these graphs that is inconsistent with our Total Escaping Power calculations, which show how much power is radiated into space by each layer of the atmosphere.
I simply deduce that, around the 15 μm, the TOA radiation is independent of the latitude and thus it is independent of the surface temperature both for Earth and Venus. In other words the atmospheres behave as a BB at 15 μm and they aren’t affected by the radiative transfer from the surface.
ReplyDeleteIn this bandwidth the atmosphere works for itself disposing of the heat that anywise enter them and assuring its thermal equilibrium.
Otherwise, how does the atmosphere get rid of the sensible/latent heat that it receive?
What happens then to the heat that is convected upwards within the troposphere?
Michele
If you look at the absorption spectra of 3-km layers of Earth's atmosphere, here you will see that the atmosphere is opaque to 15-μm radiation at an altitude of 18 km. Convection stops at an altitude of around 9 km, which we call the tropopause. At higher altitudes, ozone absorbs ultraviolet light from the sun and produces heat. Temperature increases above the tropopause. There is no convection. Heat transfer is by conduction and radiation. We are in the stratosphere. As you suggest, it is CO2 in the top of the stratosphere that radiates the stratospheric heat into space. But this is not the heat absorbed by the surface of the planet. That heat is radiated into space by the surface and the atmosphere below the tropopause.
ReplyDeleteOur calculations in With 660 ppm CO2 show that the atmosphere from 9 km to 15 km radiates more heat when we double the CO2 concentration. The same calculations, however, show a much larger decrease in the heat radiated by the lower atmosphere and the planet surface.
So, in answer to your question "What happens then to the heat that is convected upwards within the troposphere", I feel that we did a thorough job answering that question with our Total Escaping Power series of posts, in which we showed how each layer of the atmosphere on a clear day is more transparent than the layer below, so that each layer can radiated heat through the layer above.
I am a little confused.
ReplyDeleteWhat happened to your claims of Atmospheric Convection post?
Using words and formulas I coherently say only what you graphically say with your diagram. Nothing more.
Michele
Dear Michele,
ReplyDeleteI apologize for your confusion.
The Atmospheric Convection post considers convection in a simplified case, the Extreme Greenhouse, in which the "filter gas" comes to an abrupt end at a certain altitude, and is opaque to all long-wave radiation.
We eventually discover (with your help) that the temperature laps rate is equal to −g/Cp provided the heat transported is greater than zero. On Earth, most of the heat transported by convection radiates away into space before it gets to the tropopause. At the tropopause, the heat transport by convection stops and so does the laps rate.
Yours, Kevan
As far as I know the surface radiation within the bandwidth of 15 μm is completely absorbed and thermalized closest the same surface (because the CO2 extinction coefficient is very very high, that’s, the atmosphere is a BB at 15 μm) and the obtained heat goes upwards by convection.
ReplyDeleteThe radiation re-appears when the upwelling atmospheric gas stops to rise. Then, it reaches the thermal equilibrium and the CO2 (the sole which can do that at the tropopause temperature) converts the heat to radiation escaping to space.
Otherwise the atmosphere couldn’t be thermally cleaned.
Michele
What do you mean by "the radiation re-appears"?
ReplyDeleteThe radiation turns into heat. It spreads to the other gases with which the CO2 is mixed. It spreads to water vapor, which radiates heat at a variety of other wavelengths.
What do you mean by "thermally cleaned"?
“the radiation re-appears”
ReplyDeleteThe radiation can exist solely outside of the BB. The radiation entering a BB vanishes being degraded to heat. It spreads within the BB and it is transferred solely by conduction/convection. It comes back to exist at the opposite face of the BB.
“thermally cleaned”
The heat is the waste of any other form of energy that as to be collected into a rubbish tip (the tropopause) and then disposed of.
Michele
Dear Michele,
ReplyDeleteA perfect black body would radiate only at its outer surface. The atmosphere has no outer surface. It gets progressively thinner as we go up. The thicker layers below radiate heat. Some is absorbed by the layers above, but some escapes into space.
For example, in your description of radiation by CO2, try to calculate the altitude at which CO2 radiates heat into space. There is no altitude at which the CO2 is opaque, while the CO2 above is transparent.
Yours, Kevan
The outer surface of the atmosphere is the tropopause, where the real temperature and the brightness temperature coincide.
ReplyDeleteMichele
Of course the brightness temperature is also independent of the saurface temperature.
ReplyDeleteMichele
The radiation turns into heat. It spreads to the other gases with which the CO2 is mixed. It spreads to water vapor, which radiates heat at a variety of other wavelengths.
ReplyDeleteIf I am not mistaken, the water vapor emits only at the three normal modes of its free molecules (3750 – 3650 – 1600 cm-1), all intramolecular and greater than the 667 cm-1 of the CO2 and so it have nothing to do with the FIR emission. If we refer to the water droplets then the emission is due to the intermolecular bound of the quasi 2.7E21 molecules of a droplet and so it is practically in the continuum. This happens within the middle troposphere as the water droplets don’t exist within the lower and upper troposphere and within the tropopause.
Michele
Dear Michele,
ReplyDeleteI believe you are mistaken about the spectrum of water vapor. Please consult our many posts on the absorption spectrum of water vapor, such as Water Vapor Continuum, and consult our graphs of the absorption spectrum of 3-km atmospheric layers in The Earth's Atmosphere. By radiative symmetry, water vapor must radiate at the same wavelengths that it absorbs. The entire atmosphere is a gray body that absorbs and radiates long-wave radiation of all wavelengths, each to a different degree.
Yours, Kevan
I got the impression there was something strange and I have been doing a little homework.
ReplyDeleteI continue to be confused.
What happened to your UPDATE added to Vapor Versus Liquid post?
Is there a good reason of your new point of view that I cannot find or understand?
Michele
Dear Michele,
ReplyDeleteThe UPDATE is still there. I'm not sure what my "new point of view" is. If you want an introduction to the absorption spectrum of water vapor, I suggest you try Water Vapor Continuum, and the posts that follow it.
Yours, Kevan
On Earth, most of the heat transported by convection radiates away into space before it gets to the tropopause. At the tropopause, the heat transport by convection stops and so does the laps rate.
ReplyDeleteSorry, but I don’t agree with you.
I synthesized my point of view using the attached "Circulating Cell & Energies"
Neglecting the effects of the Earth’s rotation around its axis, i.e. the Coriolis forces, there exists only one circulating cell between the equator and the pole.
The cool air of the pole travels toward the equator as long as it is heated, remaining at the ground. Its gravitational energy (gz) remains constant whereas its thermal energy (CpT) and its total energy (Cpt+gz) increases.
At the equator the warm air rises until the tropopause (at circa 16-18 km) simply converting the thermal energy into the gravitational energy and maintaining constant the total energy.
Then the energized air moves toward the pole remaining at the top of the troposphere, its temperature remains constant whereas its gravitational energy continuously decreases. The height of the troposphere at the pole is about 8 km and hence the air reduces its total energy of about 10000-12000 J/kg (a very important amount). The energy tells us that the atmospheric air radiates to space almost at all within the tropopause during its travel from the equator to the pole.
At the pole the coolest air returns at the ground with a simple conversion of the gravitational energy to thermal energy (the total energy remains constant).
Then another cycle starts, and so on.
In other words the real heat transport by convection occurs within the tropopause where the air is cooled by its radiation to space.
Michele
Dear Michele,
ReplyDeleteIt's good to hear from you. You make an interesting argument, and I like your diagram. You have explained to me why it is that the tropopause is at a lower altitude at the poles. Thank you for that.
I believe you are correct when you say that there is a circulation of gas from the poles along the ground to the equator, up to the tropopause and so back at high altitude to the poles. But this will occur by adding together many circulations that are mostly vertical, so long as these circulations are mostly in the same direction as the large circulation you describe.
But let us assume, for the sake of argument, that air moves only as you describe. If you consult our Total Escaping Power post, you will see that the bottom 3-km layer of the atmosphere, which is the layer moving along the ground towards the equator, radiates almost 60 W/m2 into space, while the tropopause layer, at around 9 km, radiates only 15 W/m2.
Thus, if the air spends half its time near the ground, and half its time in the tropopause, it radiates five times as much heat while it's near the ground, and so my assertion remains correct.
The tropopause is not a sudden end to the atmosphere. It is the altitude at which there is no net heat flow upwards. This occurs in our atmosphere because there is heat generated at higher altitudes by the absorption of UV light by ozone. The stratosphere radiates as much head downwards towards the tropopause as the tropopause radiates upwards. And of course, most of this radiation is done by CO2. But the exchange if of order a few Watt per square meter, which is small compared to the few hundred Watts that the atmosphere below the tropopause radiates into space.
In our simulation, we assume a sudden end to the atmosphere. I believe this simplification is okay for now, but in the future we could make each row of cells more transparent than the one below, and see what difference it makes.
Yours, Kevan
I am content that you like my suggestion. As far as I know nobody has given a similar explanation. I am satisfied.
ReplyDeleteOk, the circulating cell that I had considered is the simplest scheme, bat this is certainly the way with which the equator heats one of the two poles. There are the Hadley and Ferrel cells and also the subtropical and polar jet streams. My cell represents only part of the real motions but it is enough to give an idea of what occurs. This aspect has to be studied deeper.
I think that it is needed that we consider the radiation and the heat exiting/exiting a volume of control. The radiation is partially wasted to heat and remains heat, the rest is transferred as radiation directly as EM waves or it is scattered. All the heat is collected at the top of the troposphere and then it is radiated to space. The mechanism of absorption/emission says in other words that the radiation transfer occurs according to the Beer-Lambert law with a partial wasting.
The idea has to be refined on.
Michele
Dear Michele,
ReplyDeleteYou say, "All the heat is collected at the top of the troposphere and then it is radiated to space."
That is not true. Less than 10% of the heat is radiated into space by the tropopause.
In our Total Escaping Power example, the lowest 3 km of the atmosphere radiates 220 W/m2 upwards. Of this, 60 W/m2 escapes into space. It is not absorbed by the atmosphere above. It never has any interaction with the atmosphere again. Within a thousandth of a second, this 60 W/m2 has passed entirely through the atmosphere and is gone forever.
The atmosphere from 9 km to 12 km, meanwhile, radiates 31 W/m2 and of this, 15 W/m2 escapes into space, while the remaining 16 W/m2 is absorbed by the gas above 12 km.
The tropopause is the highest point of convection. But it is not the only place that radiates heat. In our atmosphere, it radiates less than 10% of the total heat radiated into space.
Yours, Kevan
Always for the sake of argument.
ReplyDeleteI think that the radiative transfer must be compliant with the global energy transfer.
Let’s consider a layer thick dz within the atmosphere. At its bottom there is an enetring flux (W/m²) of heat Q=λδT/δz, of radiation I and of convected energy ρuE=ρu(CpT+gz+ …), whereas at its top exit the heat power Q+(δQ/δz)dz, the radiation I+(δI/δz)dz and the convective power ρu[E+(δE/δz)dz]. Hence the specific energy of the layer varies as δE/δt=δQ/δz+δI/δz-ρuδE/δz.
In steady state there is δQ/δz+δI/δz-ρuδE/δz=0 and if the temperature profile is linear (δQ/δz=0) we obtain that there must be δI/δz=ρuδE/δz=ρu(CpδT/δz+g).
In other words if the air is upwelling we have:
- negative δI/δz with a hyper adiabatic lapse rate, that’s the rising air uses the absorbed radiation to increase its convective energy and the radiative flux decreases because part of it is simply thermalized without re-emission;
- positive δI/δz with a hypo adiabatic lapse rate, that’s the rising air uses its convective energy to increase its radiative flux and it decelerates upward.
Then no conversion of heat to radiation occurs within the troposphere. The air converts all the absorbed heat to gravitational energy within the troposphere and it converts the gravitational energy to radiation within the tropopause.
Michele
Dear Michele,
ReplyDeleteI'm sorry, I'm confused by your conclusion, "Then no conversion of heat to radiation occurs within the troposphere." Have you looked at our Total Escaping Power post? If so, how can you claim that the troposphere does not radiate heat into space? Do you believe that the lower atmosphere is transparent, while the tropopause is opaque? Do you believe that the entire troposphere is opaque?
Water vapor in the lower troposphere is opaque to some bands of long-wave radiation. It therefore radiates heat at these same wavelengths. Some of this radiation is absorbed by the atmosphere above, but not all of it, because the atmosphere above contains less water vapor, and it will not absorb all of the radiation emitted by the water vapor below. We show this to be true by plotting the absorption spectra of the atmospheric layers. Do you disagree with our absorption plots? Are you saying that water vapor absorbs radiation but does not emit radiation? If so, then this would violate the principle of Radiative Symmetry, and therefore the Second Law.
Yours, Kevan
Keep calm, Kevan! The Radiative Symmetry is still perfectly there. In fact, it requires that the gas is both isothermal (δT/δz and then Q=0) and motionless (u=0) and so, in this case, the energies balance simply becomes δI/δz=0, i.e., the entering radiative flux equals the exiting one. Also, if the air is moving we can still have δI/δz=0 if [Q=0 AND (CpδT/δz+g)=0], that’s with an adiabatic lapse rate.
ReplyDeleteWith a not adiabatic lapse rate (but still linear), we have a continuous conversion of radiative energy to convective energy or vice versa and the heat doesn’t play any role in this dynamic creating/absorbing an its own radiation. All that without taking into account the radiative energy losses which thermalize it.
Of course, the remaining radiation (emitted by the surface at the bottom of the atmosphere) passes through the layer according to L&B law, part of the radiation is thermalized and if the lapse rate continues to be linear the heat is converted to convective energy.
Let me to point that. The BB is a surface at the boundary between a body and the neighboring void/gas, it isn’t the volume inside the body! Then, I think we can correctly say of BB only at the top of the troposphere.
Michele
Dear Michele,
ReplyDeleteSorry for delay: have been traveling. Let's look at an atmospheric layer, thickness δz.
Heat flow by conduction upwards = Q in W/m2
Q(z) = −γdT/dz
Q(z+δz) = −γ[dT/dz+δz(d2T/dz2)]
Total long-wave radiation flux upwards = I in W/m2
Velocity upwards = u m/s
Density = ρ kg/m2
Mass flow upwards = ρu in kg/m2
Enthalpy of gas = E = (CpT+gz+ …) in J/kg
Enthalpy in at base = ρuE
Enthalpy out at top = ρu[E+δz(dE/dz)].
Thus: dE/dt = δz(dQ/dz+dI/dz+ρudE/dz)
Given dE/dt = 0 we have:
dQ/dz+dI/dz+ρudE/dz = 0
At z=0, I is around 100 W/m2 (that's the radiation from the planet surface, minus all the radiation down to the planet surface from the atmosphere above) and at z=15 km its around 250 W/m2 (that's the radiation from below 15 km minus the radiation from above 15 km). So we have dI/dz = 0.01 W/m2/m.
The conductivity of air is low, so it seems to me that we can ignore Q.
Thus dI/dz+ρu(dE/dz) = 0
Suppose the velocity of air was 1 m/s upwards, with density 1 kg/m2, then we have:
0.01+dE/dz = 0
Cp(dT/dz) + g = −0.01
dT/dz = (−0.01−g)/Cp = −0.01001 K/m
Radiation of heat directly into space by the atmosphere does increase the lapse rate, but not by much. Cooling by expansion is more significant by a factor of one hundred.
You say: "The BB is a surface at the boundary between a body and the neighboring void/gas", please define what you mean by "the surface" of a black body, and please do so with an equation.
Yours, Kevan
Radiation of heat directly into space by the atmosphere does increase the lapse rate, but not by much. Cooling by expansion is more significant by a factor of one hundred.
ReplyDeleteThat’s right, the atmosphere and the radiation interact very negligibly between each other as regards the exchange of energy. Indeed, the real profile of the temperature shows that the air climbs within the troposphere with an isentropic conversion of its own thermal energy to gravitational energy.
… please define what you mean by "the surface" of a black body, and please do so with an equation.
The BB emits W/m² and so it is a surface that is the boundary of a region from what all the heat isn’t able to exit by means of the usual ways used within the same region (conduction and convection). The region is forced to use the radiation as its “extrema ratio” when it cannot do other to assure the heat transfer.
Michele
Dear Michele,
ReplyDeleteThe mass of the atmosphere is 10,000 kg/m2. By your argument, the fact that the mass of the atmosphere is measured in kg/m2 means that all the mass of the atmosphere is concentrated in an infinitely thin layer called the tropopause, or something else.
The radiation is passing out through the tropopause, but it does not originate in the tropopause. It originates from the ocean, the land, the water vapor in the lower atmosphere, the CO2 in all layers of the atmosphere, and of course from clouds as well.
Your "extrema ratio" argument is not an equation.
Yours, Kevan
We have two radiative fluxes passing through the tropopause: The one emitted by the surface which has passed through the troposphere undergoing some losses and the one created at the isothermal top of the troposphere by the CO2 which is in thermodynamic equilibrium and converts the gravitational energy to radiant energy as previously viewed while it travels from the equator to the pole.
ReplyDeleteI think that the rising air within the troposphere is too committed to convert the thermal energy to gravitational energy because it can be able also to emit. The EM waves simply pass through the tropospheric air losing part of their energy. The measured spectrum of absorption gives us the power that overcome the troposphere, i.e. the emitted power minus the lose one on the way. The EM waves are able to travel in the void and some molecules of the atmospheric gases counteract causing the losses.
Michele
Dear Michele,
ReplyDeleteWhat about the radiation emitted by the CO2 and water vapor in the layer of the atmosphere between 3 km and 6 km? On a clear spring day, this 3-km thick layer is at an average temperature of 270 K. It radiates 184 W/m2. A black body at the same temperature would radiate 301 W/m2. Of the 184 W/m2 it radiates upwards, 40 W/m2 passes all the way through the atmosphere and out into space.
Are you saying that this radiation does not exist? Are you suggesting that the atmosphere can absorb radiation without emitting radiation?
Yours, Kevan
I think the radiation is a phase transition that converts the heat to intra-molecular energy and then to EM waves. There occurs anything analogous to the evaporation. If we consider the rain water, it has a turbulent flow into the hill river, then a laminar flow in the flat lowland and at the end it stays into a closed drainage basin. Really. the flowing water evaporates anywhere, but the evaporating rate increases as the water travels from the hill to the flat and it becomes maximum into the drainage basin, where both the water and the air above are motionless and there is possible that the air becomes saturated of water vapour within the boundary layer.
ReplyDeleteSo, the rising air can radiate but with a rate more lesser than the one given by Planck and SB laws (I think in a negligible way). How is it possible to take into account that?
Also, the radiation power (the Poynting vector) is a complex quantity, then there acts a reactive component (power continuously exchanged without useful effect as transfer or heat) that induces the increase of the apparent power and then of the emitting temperature. What is the role that it can play in the radiative transfer?
I think the Planck and SB laws are not right and they need some corrective additional form.
Michele