Planetary Greenhouse

We now enhance our Extreme Greenhouse to produce a more interesting model. We incorporate the decrease in atmospheric pressure with altitude. We use our understanding of atmospheric convection to determine how atmospheric temperature changes with pressure. We enhance the properties of our greenhouse gas by making it transparent to some long-wave radiation. The result is a simple model of a Planetary Greenhouse, as shown below.



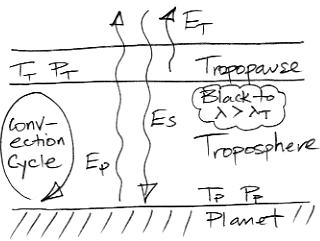
In our new model, the atmosphere continues to infinite altitude, getting thinner and thinner as we go. The lowest layer of the atmosphere is the troposphere. Above the troposphere is the tropopause. The tropopause is the layer that radiates heat into space. Above the tropopause, the atmosphere is so thin that it is transparent.

For now, we ignore day and night, and we ignore clouds. We ignore heat flowing through the solid mass of the planet. Short-wave radiation arriving from the sun passes straight through the atmosphere and is of uniform and constant power E_S. The temperature and pressure at the planet surface are T_p and P_p respectively. A near-adiabatic convection cycle carries heat up through the troposphere to the tropopause, where it is radiated into space. The temperature and pressure of the tropopause are T_T and P_T respectively.

In our Extreme Greenhouse, the atmosphere was entirely opaque to all long-wave radiation. In our new Planetary Greenhouse, the atmosphere is transparent to all radiation with wavelength less than some threshold, λ_T. At greater wavelengths, a trace greenhouse gas in the atmosphere absorbs radiation. The greater the concentration of this greenhouse gas, the shorter the absorption length of the atmosphere for wavelengths greater than λ_T. As we saw in The Upper Gas, the shorter the absorption length, the lower the tropopause pressure. As we saw in Atmospheric Convection, the lower the tropopause pressure, the lower its temperature.

As in our Extreme Greenhouse, we assume that the planet radiates like a black body. The radiation it emits below λ_T passes out into space. This radiated power is E_P. As we described in Black Bodies, we can use Plank's Law to determine the power radiated at all wavelengths, so we can calculate the power radiated below λ_T as a function of T_P.

The atmospheric convection cycle allows us to calculate the temperature of the tropopause given only T_P and the ratio P_T/P_P. The tropopause radiates power E_T into space. Using Plank's Law and radiative symmetry, we can calculate the power radiated by the tropopause as a function of T_T. The atmosphere emits radiation only at wavelengths greater than λ_T.

For thermal equilibrium, we must have the total power radiated outward by the body and the tropopause equal to the total power arriving from the sun. Thus we must have E_S = E_P + E_T. And so we arrive at a robust model of the planetary greenhouse effect when the greenhouse gas has a step-like absorption spectrum. Given only λ_T and P_P, we can plot a graph of E_P + E_T versus temperature. This graph crosses E_S at the equilibrium value of T_P. We wrote a computer program to calculate E_P + E_T versus T_P for a range of tropopause pressures. You will find the program here.

In our next post, we will choose useful values for λ_T and E_S, and we will see how doubling the concentration of our greenhouse gas affects the temperature of the planet.