Evaporation Rate

We are preparing to add evaporation from surface water to our Circulating Cells program. Water will leave the surface and enter the atmosphere as water vapor. The rate at which water evaporates depends upon the humidity and movement of the air above. The following empirical equation, which we found here, tells us the approximate rate at which water will evaporate into air, assuming the air is at roughly the same temperature as the water.

w = (0.007 + 0.005v)(x_s − x),

where w is the evaporation rate in grams per second for each square meter of water surface (g/m²s), v is the velocity of the air in meter per second (m/s), x_s is the saturation concentration of water vapor in grams of water per kilogram of dry air (g/kg) for air at the same temperature as the water, and x is the actual concentration of water vapor in grams per kilogram of dry air (g/kg) in the air above the water.

In our simulation, we know the temperature of the surface water, and when we simulate a planet with a water surface using CC8, we find that the surface gas cells are within a few degrees of the temperature of the surface water. Our previous work on impetus for circulation suggests that the velocity of our gas cells is of order 4 m/s. When we implement evaporation, we will keep track of the water vapor concentration in each cell, so we will know x. What remains for us to determine is x_s, the saturation concentration of water vapor in air at the surface temperature.

The following graph shows measured values of saturation concentration in g/kg for a range of temperatures in Kelvin, based upon data we found here. To see the same plot in Centigrade, see here.



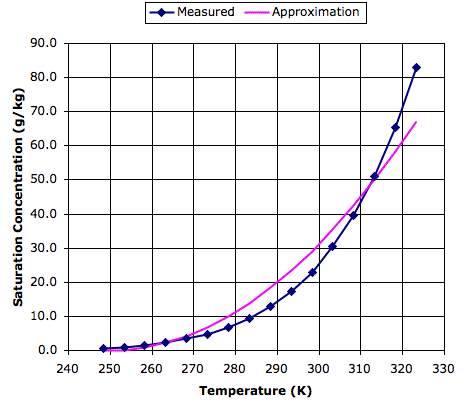
Also plotted on the graph is a parabolic approximation to the measured data, which is based upon two reference points: 0 g/kg at 250 K and 45 g/kg at 310 K. This approximation is good enough for our purposes, and will simplify our program. Thus our evaporation equation becomes:

w = [(T−250)²/80 − x] / 40

For example, if we have dry air over a lake at 290 K (14°C), water will evaporate at 0.5 g/m²s. In one hour, 1.8 kg of water will evaporate from each square meter. Our gas cells have mass 330 kg/m², so after an hour over the lake, the gas will acquire water vapor concentration 5 g/kg, which is well below the saturation concentration of 20 g/kg given by our approximation. Its relative humidity will be 25%.