In our previous post, we concluded that air above the desert cools down by 10°C in the first hour after sunset because cold air descends slowly from above as the day's convection cycle comes to a stop. This explanation is not one of the several you will find on the web if you search for "Why does the desert get so cold at night?" These other explanations talk about dry air allowing heat to radiate away into space. But our calculations in Day and Night showed that the rate at which the Earth and its atmosphere radiate heat is barely adequate to cool the air by half a degree in ten hours, let alone ten degrees in one hour.
One of our readers points us to another night-time cooling phenomenon called "night inversion". According to this description, the air immediately above a forest can be 10°C cooler at night than the air 100 m up. In our explanation of the desert cooling, the cold air above the desert was still warmer than the air higher up, but in this case, the air above the forest is actually colder than the air higher up. We will conclude our Surface Cooling series by offering an explanation for nigh inversion also.
The first 100 m of the atmosphere has heat capacity 100 kJ/K/m2. The forest is a good black body, so it will radiate of order 100 W/m2 directly into space through a clear night sky. A leaf, being roughly 1 mm thick, and consisting mostly of water, has heat capacity roughly 4 kJ/K/m2. When it radiates 100 W/m2 it will tend to cool by more than 1°C every minute. It is the heat capacity of the air around it that will stop the leaf from freezing.
The forest leaves will set up a convection cycle in which air is cooled by the upper leaves, which are the ones radiating into space, and warmed by the surface of the Earth below. The air immediately above the forest will be sucked into this cycle, and the air immediately above that also, so that the very cold air of the tree-tops mixes slowly with the air ten to a hundred meters up, creating a layer of air that is colder and more dense than the air above. The convection cycle transports roughly 100 W/m2. Suppose that the mixing we describe causes 30 W/m2 to be removed from the heat capacity of the first 100 m of air. In that case, the average temperature of the first 100 m will drop by 5°C in six hours.
So we see that radiation by leaves held ten or twenty meters above the ground can cause the first hundred meters of the atmosphere to cool by several degrees compared to the air above, and so create a static, cold layer of air above the forest. If there is any wind, of course, the leaves will no longer need their convection cycle to keep them warm: the wind will warm them, and blow away any cold air as well. The night must be still for such inversion to take place, and air is more often still in a bowl or valley.
Our Surface Cooling posts have introduced us to the heat capacity of the atmosphere, and shown us that traditional explanations for cooling and warming may be unreliable. But we have no proof that it is an exchange of warm air for cold air that causes the sudden drop in temperature at sunset in the desert. Nor do we have any proof that a cold convection cycle in a forest causes night inversion. Both explanations are merely hypotheses. Any help devising experiments to test either hypothesis would be much appreciated. Our ideas so far, which involve helium balloons and battery-powered thermometers, appear impractical, not to mention expensive.
Thursday, December 30, 2010
Tuesday, December 21, 2010
Surface Cooling, Part III
UPDATE: The original version of this post included an argument by Second Law of Thermodynamics that, although correct, did not point out the actual physical mechanism by which desert air cools at sunset. I cut out this argument and added a description of the physical mechanism as suggested by my father.
The air above the desert cools by 20°C at night. But the heat capacity of the air above the desert is so great that it is impossible for it to cool so quickly by radiation into space or by conduction to the ground. We ended our previous post with the suggestion that the drop in temperature over the desert at night is caused not by the cooling of air, but by the replacement of warm air by cold air.
In Biggles Flies South, the author tells us that flying over the desert during the day is exhausting and uncomfortable because the air is so "bumpy". The best time to fly is the early morning, when the air is still and there is daylight to see by. Our understanding of atmospheric convection suggests that the air above the desert will be a succession of convection cycles, something like the drawing below, where small features of the surface end up dictating the boundaries of the cycles, and the cycles are angled sideways by a prevailing wind.
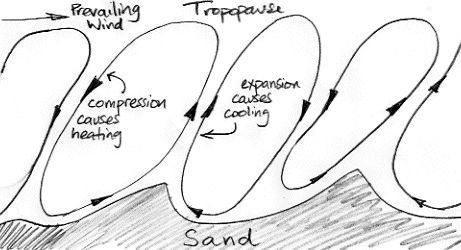
All this convection is caused by the sun heating the desert sand until it warms the air and causes the air to rise. But when the sun goes down, the sand cools off quickly. The circulation will eventually come to a stop, but it's momentum will keep it going for a while. When it is near to stopping, air is descending slowly from above, and comes to a stop. The sand is no longer hot, and no longer warms the air.
When the sun goes down over the desert, the day-time convection of the atmosphere slows to a halt. The slowing cycle brings cold air down from above. This cold air is not warmed by the hot sand as it would be during the day. The temperature drops by ten or twenty degrees in an hour. For the rest of the night, the air is still and cools slowly by radiating into space. Perhaps the temperature will drop by another one or two degrees by dawn.
The air above the desert cools by 20°C at night. But the heat capacity of the air above the desert is so great that it is impossible for it to cool so quickly by radiation into space or by conduction to the ground. We ended our previous post with the suggestion that the drop in temperature over the desert at night is caused not by the cooling of air, but by the replacement of warm air by cold air.
In Biggles Flies South, the author tells us that flying over the desert during the day is exhausting and uncomfortable because the air is so "bumpy". The best time to fly is the early morning, when the air is still and there is daylight to see by. Our understanding of atmospheric convection suggests that the air above the desert will be a succession of convection cycles, something like the drawing below, where small features of the surface end up dictating the boundaries of the cycles, and the cycles are angled sideways by a prevailing wind.

All this convection is caused by the sun heating the desert sand until it warms the air and causes the air to rise. But when the sun goes down, the sand cools off quickly. The circulation will eventually come to a stop, but it's momentum will keep it going for a while. When it is near to stopping, air is descending slowly from above, and comes to a stop. The sand is no longer hot, and no longer warms the air.
When the sun goes down over the desert, the day-time convection of the atmosphere slows to a halt. The slowing cycle brings cold air down from above. This cold air is not warmed by the hot sand as it would be during the day. The temperature drops by ten or twenty degrees in an hour. For the rest of the night, the air is still and cools slowly by radiating into space. Perhaps the temperature will drop by another one or two degrees by dawn.
Wednesday, December 15, 2010
Surface Cooling, Part II
In our Surface Cooling, Part I, we saw that the air above the ocean cools by less than 1°C at night. The air above the desert in Arizona, however, cools by 20°C at night. In Night and Day we saw that the heat radiated into space by the Earth is barely sufficient to cool the atmosphere by 1°C at night, let alone 20°C, so we are left wondering how the air above the desert can cool down so fast.
The table below presents the thermal properties of some common surface materials. We will make use of this table in future posts. Values for composite materials like wet soil are approximate. We picked values that are representative from resources like this, this, and this. Today we will use only the properties of dry sand. In the first column we have the thermal conductivity in Watt per meter per Kelvin (W/mK = W/m°C). A layer of material with thermal conductivity α, thickness d, temperature Tb at the bottom and Tt at the top, will conduct α(Tb−Tt)/d for each square meter of its surface area. A 10-cm thick layer of dry sand that is 20°C cooler on top than bottom will conduct 0.20 W/mK × 20 °C / 0.1 m = 40 W/m2.
Our SC1 program simulates the cooling of the surface of the Earth at night. You can download it and run it yourself, by following the instructions in the code. The program works by dividing the surface material into thin layers and calculating the temperature of each layer in a sequence of small time steps. We assume the material is at a uniform temperature when it begins to cool, and that the heat loss from the upper surface is a constant 200 W/2. In earlier versions of the code, we calculated the surface loss as a combination of radiation into space and convection with the surface air, but our results were pretty much the same, so we reverted to the assumption of constant loss to keep things simple.
The following graph shows what our simulation program tells us happens to dry sand at various depths in millimeters when it starts to cool from the surface at 200 W/m2. We see the surface cools by 13°C in 1000s while the sand 40 mm down cools by roughly 0.1°C.
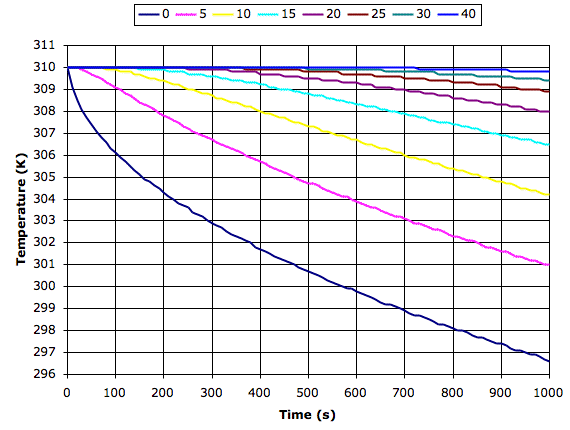
Materials with greater conductivity cool more slowly because heat rises from below to keep the surface warm. If we apply our simulation program to sandstone or asphalt, we find the surface cools down ten times more slowly than the surface of dry sand. So it is above dry sand or soil that we expect to see the greatest drop in surface temperature at night.
Our calculations show that a sandy surface can cool by 20°C at night. They show that one meter down, the heat of the day will hardly affect the temperature of the sand. But they still don't explain why the temperature above the desert sand cools by 20°C at night. The surface of the sand cools down because it loses heat to the air and to outer space. If anything, the cooling sand warms the air. We already know that the heat radiated by the air itself is not sufficient to cause such cooling. Indeed, our calculations show that it is impossible for air above the desert to cool by 20°C at night. And yet we know that a thermometer 2 m above the surface of the desert can register a drop of 20°C.
We conclude that the air above the sand at night cannot be the same air above the sand during the day, and indeed this conclusion leads us to a most satisfactory explanation for cold desert nights.
The table below presents the thermal properties of some common surface materials. We will make use of this table in future posts. Values for composite materials like wet soil are approximate. We picked values that are representative from resources like this, this, and this. Today we will use only the properties of dry sand. In the first column we have the thermal conductivity in Watt per meter per Kelvin (W/mK = W/m°C). A layer of material with thermal conductivity α, thickness d, temperature Tb at the bottom and Tt at the top, will conduct α(Tb−Tt)/d for each square meter of its surface area. A 10-cm thick layer of dry sand that is 20°C cooler on top than bottom will conduct 0.20 W/mK × 20 °C / 0.1 m = 40 W/m2.
Conductivity Density CapacityThe second column gives the density in kilogram per cubic meter (kg/m3). A 10-cm layer of dry sand has mass 0.1 m × 1700 kg = 170 kg/m2. The third column gives the specific heat capacity in Joule per kilogram per kelvin ( J/kgK = J/kg°C). A layer of material with specific heat capacity C, density ρ, and thickness d will require Cρd Joules of heat per square meter of surface area to raise its temperature by 1°C. A 10-cm thick layer of dry sand requires 800 J/kgK × 1700 kg × 0.1 m = 136 kJ/m2 to warm up by 1°C. Alternatively, we must remove 136 kJ/m2 to cool it by 1°C. If this layer loses loses 80 W/m2, it will take half an hour to cool down by 1°C.
Material (W/mK) (kg/m^3) (J/kgK)
Air 0.024 1.2 1000
Asphalt 0.75 1300 920
Copper 390 8900 420
Ice 2.2 910 2000
Mercury 8.7 14000 140
Sand, Dry 0.20 1600 830
Sand, Wet 4.0 2000 2500
Sandstone 1.7 2500 800
Soil, Dry 0.4 1300 1400
Soil, Wet 4.0 1500 2500
Snow, Light 0.10 100 420
Steel 43 7800 460
Water 0.58 1000 4200
Wood, Oak 0.17 770 1700
Our SC1 program simulates the cooling of the surface of the Earth at night. You can download it and run it yourself, by following the instructions in the code. The program works by dividing the surface material into thin layers and calculating the temperature of each layer in a sequence of small time steps. We assume the material is at a uniform temperature when it begins to cool, and that the heat loss from the upper surface is a constant 200 W/2. In earlier versions of the code, we calculated the surface loss as a combination of radiation into space and convection with the surface air, but our results were pretty much the same, so we reverted to the assumption of constant loss to keep things simple.
The following graph shows what our simulation program tells us happens to dry sand at various depths in millimeters when it starts to cool from the surface at 200 W/m2. We see the surface cools by 13°C in 1000s while the sand 40 mm down cools by roughly 0.1°C.

Materials with greater conductivity cool more slowly because heat rises from below to keep the surface warm. If we apply our simulation program to sandstone or asphalt, we find the surface cools down ten times more slowly than the surface of dry sand. So it is above dry sand or soil that we expect to see the greatest drop in surface temperature at night.
Our calculations show that a sandy surface can cool by 20°C at night. They show that one meter down, the heat of the day will hardly affect the temperature of the sand. But they still don't explain why the temperature above the desert sand cools by 20°C at night. The surface of the sand cools down because it loses heat to the air and to outer space. If anything, the cooling sand warms the air. We already know that the heat radiated by the air itself is not sufficient to cause such cooling. Indeed, our calculations show that it is impossible for air above the desert to cool by 20°C at night. And yet we know that a thermometer 2 m above the surface of the desert can register a drop of 20°C.
We conclude that the air above the sand at night cannot be the same air above the sand during the day, and indeed this conclusion leads us to a most satisfactory explanation for cold desert nights.
Wednesday, December 8, 2010
Surface Cooling, Part I
In Day and Night we found that the heat capacity of the atmosphere keeps the Earth warm at night. There are ten tons of air above every square meter of the Earth, and this ten tons has heat capacity 10 MJ/°C. When the atmosphere radiates 200 W/m2 into space, which is typical of a clear sky, its average temperature drops by less than 1°C in twelve hours.
The heat capacity of water, meanwhile, keeps a pond warm at night. In a 1-m deep pond, there is a ton of water beneath every square meter of surface, and this ton has heat capacity 4 MJ/°C. If the water surface radiates 80 W/m2 into space, which is typical when the sky is clear, this radiation will cool the pond by less than 1°C in twelve hours. The water surface will, of course, be losing more heat by atmospheric convection and by evaporation. But in the ocean, where the top ten meters of water are well-mixed by waves, even a surface loss of 800 W/m2 will cool the water by less than 1°C at night.
Here is a twenty-day recording of air and water temperature from an ocean buoy, which we obtained from the National Data Buoy Center. The data is here.
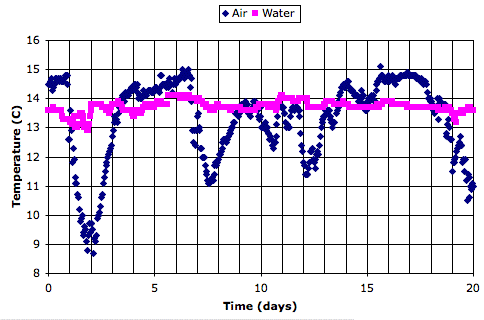
We see that the air temperature varies by 5°C from one week to the next, but by less than 1°C from day to night. The water itself, meanwhile, is hardly affected by the weekly variations, and not at all by the daily variations.
Why, then, does the temperature in Arizona drop by 20°C at night? The surface of Arizona is sand and rocks. These solid, opaque materials transport heat within themselves by conduction alone. During the day, their surfaces get hot. During the night, they cool down. In our next post, we will present the thermal properties of some common surface materials, along with a computer program to calculate how fast these surface materials will cool at night. We will find out whether the thermal properties of sand can explain why the desert is hot in the day and cold at night.
The heat capacity of water, meanwhile, keeps a pond warm at night. In a 1-m deep pond, there is a ton of water beneath every square meter of surface, and this ton has heat capacity 4 MJ/°C. If the water surface radiates 80 W/m2 into space, which is typical when the sky is clear, this radiation will cool the pond by less than 1°C in twelve hours. The water surface will, of course, be losing more heat by atmospheric convection and by evaporation. But in the ocean, where the top ten meters of water are well-mixed by waves, even a surface loss of 800 W/m2 will cool the water by less than 1°C at night.
Here is a twenty-day recording of air and water temperature from an ocean buoy, which we obtained from the National Data Buoy Center. The data is here.

We see that the air temperature varies by 5°C from one week to the next, but by less than 1°C from day to night. The water itself, meanwhile, is hardly affected by the weekly variations, and not at all by the daily variations.
Why, then, does the temperature in Arizona drop by 20°C at night? The surface of Arizona is sand and rocks. These solid, opaque materials transport heat within themselves by conduction alone. During the day, their surfaces get hot. During the night, they cool down. In our next post, we will present the thermal properties of some common surface materials, along with a computer program to calculate how fast these surface materials will cool at night. We will find out whether the thermal properties of sand can explain why the desert is hot in the day and cold at night.
Wednesday, December 1, 2010
Day and Night
In a previous post, we considered the dramatic change in the temperature of the moon as it revolves around the Earth. In the middle of its night, the moon cools to −190 °C. In the middle of its day, it warms to 100 °C. I was in Phoenix, Arizona last week. The sky was clear all day and all night, and the air was dry. In the middle of the night, the temperature dropped to 0°C. In the middle of the day, it rose to 20°C. The day-night variation on the moon is 290°C, but on the Earth it is only 20°C.
The moon's days are one month long. At night, the surface rocks have time to cool down, losing all the heat they gained during the day. They get so cold they draw heat out of the moon's interior, and this flow of heat from the depths of the moon is what stops the moon's surface from dropping below −190°C. During the day, the rocks heat up until they start to radiate almost as much heat as is arriving from the Sun. But some heat flows into the depths of the moon to make up for the heat drawn out during the previous night.
The moon has no atmosphere, so the only thing stopping it from cooling down to absolute zero at night is the heat capacity and thermal conductivity of its surface rocks. On Earth, we have the heat capacity of the atmosphere to keep the surface warm during the night. Above each square meter of the Earth's surface is 10,000 kg of air (see Atmospheric Weight). The heat capacity of dry air is is roughly 1 kJ/K/kg. So the air above each square meter of the Earth has heat capacity 10 MJ. The Earth and its atmosphere radiate something like 250 W/m2 into space. Suppose this 250 W/m2 were extracted uniformly from the entire column of air above each square meter of the surface. It would take 10 MJ ÷ 250 W = 10 hrs to cool the air by 1°C.
We see that the heat capacity of the atmosphere is significant in reducing the temperature changes caused by the setting of the sun or the formation of thick clouds. Indeed, the temperature changes we observe from day to night on Earth are more than ten times greater than our simple heat capacity calculation suggests. Perhaps if we consider the individual 3-km layers of the atmosphere, we will come up with a different answer.
As day turns to night, the Sun no longer warms the Earth, but the Earth and its atmosphere continue to radiate heat into space. The following table gives the escaping power in Watts per square meter from each 3-km layer of the Earth's atmosphere up to the tropopause, as calculated by our TEP2 program under conditions we describe here.
Let us ignore the heat passing up through the atmosphere by radiation and convection, and assume that the Earth's surface starts to lose 80 W/m2 when the sun sets. Suppose the surface itself is water 1 m deep. The heat capacity of water is roughly 4 kJ/K/kg and its density is 1,000 kg/m3. Beneath each square meter is fluid with heat capacity 4 MJ/K. This water will cool by only 1 °C in 10 hrs.
The 0-km layer radiates 46 W/m2 directly into space. The mass of air in this first 3-km layer is a little less than 3,000 kg, with heat capacity roughly 3 MJ/K. At a loss of 46 W/m2, this layer will cool down by only 0.5°C in ten hours.
The changes in temperature we observe at the surface of the Earth from day to night are much greater than we would expect from a consideration of the heat capacity of the atmosphere and total escaping power alone. What is going on when the sun sets, that makes the Earth's surface cool down so fast? We will hope to answer this question in our next post.
The moon's days are one month long. At night, the surface rocks have time to cool down, losing all the heat they gained during the day. They get so cold they draw heat out of the moon's interior, and this flow of heat from the depths of the moon is what stops the moon's surface from dropping below −190°C. During the day, the rocks heat up until they start to radiate almost as much heat as is arriving from the Sun. But some heat flows into the depths of the moon to make up for the heat drawn out during the previous night.
The moon has no atmosphere, so the only thing stopping it from cooling down to absolute zero at night is the heat capacity and thermal conductivity of its surface rocks. On Earth, we have the heat capacity of the atmosphere to keep the surface warm during the night. Above each square meter of the Earth's surface is 10,000 kg of air (see Atmospheric Weight). The heat capacity of dry air is is roughly 1 kJ/K/kg. So the air above each square meter of the Earth has heat capacity 10 MJ. The Earth and its atmosphere radiate something like 250 W/m2 into space. Suppose this 250 W/m2 were extracted uniformly from the entire column of air above each square meter of the surface. It would take 10 MJ ÷ 250 W = 10 hrs to cool the air by 1°C.
We see that the heat capacity of the atmosphere is significant in reducing the temperature changes caused by the setting of the sun or the formation of thick clouds. Indeed, the temperature changes we observe from day to night on Earth are more than ten times greater than our simple heat capacity calculation suggests. Perhaps if we consider the individual 3-km layers of the atmosphere, we will come up with a different answer.
As day turns to night, the Sun no longer warms the Earth, but the Earth and its atmosphere continue to radiate heat into space. The following table gives the escaping power in Watts per square meter from each 3-km layer of the Earth's atmosphere up to the tropopause, as calculated by our TEP2 program under conditions we describe here.
--------------------------------------------------The surface of the Earth radiates 390 W/m2. Of this, 80 W/m2 escapes directly into space. The rest of it is absorbed by the atmosphere. But the atmosphere radiates heat towards the surface also. The 0-km layer (the first 3 km of the atmosphere) radiates 260 W/m2 upwards and downwards. We may have thought only of the upward component in the past, but the downward component exists also, and is equal to the upward component.
Name Temp BB Layer Escaping
--------------------------------------------------
Surface 290.0 401.1 388.8 80.0
0-km 280.0 348.5 262.6 46.1
3-km 270.0 301.3 184.8 39.7
6-km 250.0 221.5 111.5 44.6
9-km 230.0 158.7 50.7 26.4
12-km 220.0 132.8 22.2 10.1
15-km 220.0 132.8 14.4 5.5
--------------------------------------------------
Total: 252.5
--------------------------------------------------
Let us ignore the heat passing up through the atmosphere by radiation and convection, and assume that the Earth's surface starts to lose 80 W/m2 when the sun sets. Suppose the surface itself is water 1 m deep. The heat capacity of water is roughly 4 kJ/K/kg and its density is 1,000 kg/m3. Beneath each square meter is fluid with heat capacity 4 MJ/K. This water will cool by only 1 °C in 10 hrs.
The 0-km layer radiates 46 W/m2 directly into space. The mass of air in this first 3-km layer is a little less than 3,000 kg, with heat capacity roughly 3 MJ/K. At a loss of 46 W/m2, this layer will cool down by only 0.5°C in ten hours.
The changes in temperature we observe at the surface of the Earth from day to night are much greater than we would expect from a consideration of the heat capacity of the atmosphere and total escaping power alone. What is going on when the sun sets, that makes the Earth's surface cool down so fast? We will hope to answer this question in our next post.
Tuesday, November 23, 2010
Adiabatic Magic
A while back, a visitor here tried to persuade us that heat flow through an atmosphere was not required to make it warmer at the bottom than the top. He was convinced that adiabatic circulation would always take place within the atmosphere, regardless of whether or not heat was flowing, and this circulation would always make the bottom warmer than the top. At Science of Doom, meanwhile, several authors try to convince us that the surface of Venus will be super-hot even if it is not being heated by the Sun. They describe some kind of adiabatic process, which we will call adiabatic magic, by which any atmosphere will always be warmer at the bottom than the top, even with no heat flow. Indeed, one author goes so far as to say that heat flow from bottom to top will actually decrease the temperature difference between the lower and upper atmosphere.
We are well aware that air taking part in atmospheric convection will cool down as it rises, and warm up as it falls, but this circulation is powered by heat absorbed from the planet and subsequently radiated into space by the atmosphere. It is not spontaneous or self-generated. The circulation requires that the planet surface be warmed by the sun and that the atmosphere be capable of radiating heat into space at higher altitudes. With no heat flow, there will be no circulation, and no temperature difference between top and the bottom of the atmosphere. In other words: there is no such thing as adiabatic magic, as we will now demonstrate.
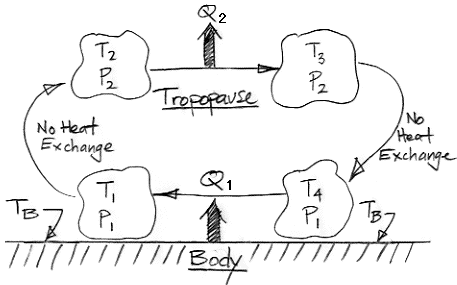
The diagram below shows how we can use adiabatic magic to create a machine that is 100% efficient at turning heat into work. Such a machine is also known as a perpetual motion machine of the second kind.
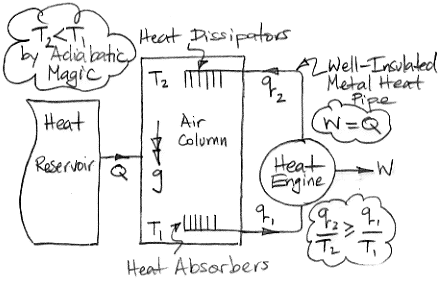
In the center of the diagram is an air column. The action of gravity is indicated by the double-headed arrow with the letter g. The column is high enough that the weight of the air it contains causes the pressure to be greater at the bottom than the top. By adiabatic magic, the bottom of the column is hotter than the top, so T1 > T2. We exploit this temperature difference with a heat engine. Metal veins absorb heat from the air at base of the column. A metal rod, well-clad with thermal insulation, carries this heat to a heat engine. A heat engine is something like a steam turbine, which exploits the flow of heat from hot to cold in order to generate work. Heat flows out of the engine through another metal rod to top of the column. The heat flowing into the engine is q1 and the heat flowing out is q2. The work produced by the heat engine is W. We express the heat flow and work output in Watts.
The First Law of Thermodynamics requires that W = q1 − q2. The Second Law of Thermodynamics requires that the entropy of the heat going in must be less than or equal to the entropy of the heat going out. With the absolute temperature scale, this means that q1 / T1 ≤ q2 / T2. Subject to these constraints, we see that our heat engine can produce work by exploiting the temperature difference between the bottom and the top of the air column.
Of course, we are taking more heat out of the bottom of the column than we are restoring to the top, so the total heat of the column will tend to decrease. We're not sure what the adiabatic magic theory has to say about an air column as it cools, so we are going to avoid this issue by adding heat to the column from a large reservoir. We add exactly as much heat as the column is losing by the action of the heat engine. The heat we add is Q, so Q = q1 − q2 = W.
So now let us consider the air column and the heat engine acting together. They constitute a perpetual motion machine. We see that we have Q entering the machine and W leaving. The machine turns heat into work with 100% efficiency. It is a perpetual motion machine of the second kind.
The adiabatic magic idea is one of a class of impossible ideas: those that propose the spontaneous separation of heat into hot and cold. The above diagram could be adapted to disprove any such idea with equal facility. If someone claimed they had invented a new material that always became hotter at one end than the other, even with no heat flow from one end to the other, we could disprove his claim with the above diagram.
Because adiabatic magic is impossible, we see that a transparent atmosphere can be no warmer at the bottom than at the top. Transparent gas cannot radiate heat into space (see Radiative Symmetry). In the case of Venus, if nothing heats the surface, the gas at the surface will be no warmer than the gas at the altitude to which sunlight does penetrate.
Of course, our atmosphere does radiate heat into space, so the lower air is warmer than the upper air, in order to transport that heat. And Venus's atmosphere gets hotter all the way to the surface, which means it is transporting heat away from the surface and radiating it into space.
We are well aware that air taking part in atmospheric convection will cool down as it rises, and warm up as it falls, but this circulation is powered by heat absorbed from the planet and subsequently radiated into space by the atmosphere. It is not spontaneous or self-generated. The circulation requires that the planet surface be warmed by the sun and that the atmosphere be capable of radiating heat into space at higher altitudes. With no heat flow, there will be no circulation, and no temperature difference between top and the bottom of the atmosphere. In other words: there is no such thing as adiabatic magic, as we will now demonstrate.
The diagram below shows how we can use adiabatic magic to create a machine that is 100% efficient at turning heat into work. Such a machine is also known as a perpetual motion machine of the second kind.

In the center of the diagram is an air column. The action of gravity is indicated by the double-headed arrow with the letter g. The column is high enough that the weight of the air it contains causes the pressure to be greater at the bottom than the top. By adiabatic magic, the bottom of the column is hotter than the top, so T1 > T2. We exploit this temperature difference with a heat engine. Metal veins absorb heat from the air at base of the column. A metal rod, well-clad with thermal insulation, carries this heat to a heat engine. A heat engine is something like a steam turbine, which exploits the flow of heat from hot to cold in order to generate work. Heat flows out of the engine through another metal rod to top of the column. The heat flowing into the engine is q1 and the heat flowing out is q2. The work produced by the heat engine is W. We express the heat flow and work output in Watts.
The First Law of Thermodynamics requires that W = q1 − q2. The Second Law of Thermodynamics requires that the entropy of the heat going in must be less than or equal to the entropy of the heat going out. With the absolute temperature scale, this means that q1 / T1 ≤ q2 / T2. Subject to these constraints, we see that our heat engine can produce work by exploiting the temperature difference between the bottom and the top of the air column.
Of course, we are taking more heat out of the bottom of the column than we are restoring to the top, so the total heat of the column will tend to decrease. We're not sure what the adiabatic magic theory has to say about an air column as it cools, so we are going to avoid this issue by adding heat to the column from a large reservoir. We add exactly as much heat as the column is losing by the action of the heat engine. The heat we add is Q, so Q = q1 − q2 = W.
So now let us consider the air column and the heat engine acting together. They constitute a perpetual motion machine. We see that we have Q entering the machine and W leaving. The machine turns heat into work with 100% efficiency. It is a perpetual motion machine of the second kind.
The adiabatic magic idea is one of a class of impossible ideas: those that propose the spontaneous separation of heat into hot and cold. The above diagram could be adapted to disprove any such idea with equal facility. If someone claimed they had invented a new material that always became hotter at one end than the other, even with no heat flow from one end to the other, we could disprove his claim with the above diagram.
Because adiabatic magic is impossible, we see that a transparent atmosphere can be no warmer at the bottom than at the top. Transparent gas cannot radiate heat into space (see Radiative Symmetry). In the case of Venus, if nothing heats the surface, the gas at the surface will be no warmer than the gas at the altitude to which sunlight does penetrate.
Of course, our atmosphere does radiate heat into space, so the lower air is warmer than the upper air, in order to transport that heat. And Venus's atmosphere gets hotter all the way to the surface, which means it is transporting heat away from the surface and radiating it into space.
Tuesday, November 16, 2010
Condensation and Convection
One of our readers has been asking me about the role of condensation in accelerating convection, as described in papers like this one. So let us dicsuss the effect of evaporation and condensation in convection.
Consider a kilogram of air that has just been warmed at the surface of the Earth, and is now rising towards the tropopause as part of atmospheric convection. This kilogram has temperature 300 K, pressure 100 kPa, and volume 860 l (liters). Let us suppose this air contains 10 l of water vapor. This water vapor has mass 10 g and would occupy 10 ml (milliliters) if it condensed into liquid.
Our rising volume of air expands and cools. Its pressure drops to 50 kPa and its temperature to 250 K. It expands to 1400 l. At this temperature, almost all of our water must condense into liquid. Before condensation, the water occupies 14 l. When it condenses it will turn into microscopic water droplets that occupy only 14 ml. Of course, these droplets will freeze afterwards, but let's ignore that for now, and consider what happens when the water first condenses.
Most likely, the condensation will occur gradually as the air expands, but we will imagine that it happens after the expansion is complete, so we can calculate the net effect of condensation upon the pressure of our gas. At the end of the expansion, our air contains supersaturated water vapor, like the gas in a cloud chamber.
Consider the first gram of water that condenses. Let us assume, for the time being, that this condensation happens instantly, so that our two cubic meters of air has no time to expand or contract during the process. That is to say: we assume the condensation takes place at constant volume.
Before condensation, this one gram occupied 1.4 l in our volume of 1400 l. After condensation, the water droplets occupy a combined volume of only 1 ml. The remaining air and water vapor expand into our 1400 l. As it expands, its pressure decreases by 0.1%.
When water condenses, it gives up its latent heat of evaporation, which is 2 MJ/kg. When the first gram of water condenses, it gives up 2 kJ of heat to our 1400 l of air. The heat capacity of air at constant volume is roughly 700 kJ/kgK, so our kilogram of air warms up by around 3 K. It's pressure increases by 3 K ÷ 250 K = 1.2%.
We see that the first gram of water condensation causes a net increase in pressure of 1.2% - 0.1% = 1.1% in our kilogram of air. Suppose the air all around is dry. It has not been warmed by condensation. It's pressure has not increased. Our two cubic meters pushes outwards with its greater pressure and expands until it's pressure is the same as that of the surrounding air. It will expand by 1.1%. Its 1 kg of mass will occupy the same volume as 1.011 kg of surrounding dry air. It will experience an upward buoyancy force of 11 g weight, or 0.11 N. This force will cause it to accelerate upwards at 0.11 m/s2. Within less than a minute, it will be traveling upwards at a few meters per second. At that point, other forces will come into play to slow it down. We note that we allowed only 1 g of our water vapor to condense. If all 10 g condensed at once, our kilogram of air would experience ten times more lift.
We see that condensation does indeed cause air to rise more quickly than surrounding dry air.
Moist air will expand more than dry air as it rises towards the tropopause. Evaporation, on the other hand, causes air to rise more slowly. Air at the surface of a dry desert heats up fast in contact with the hot sand. It rises quickly. We get dust devils and sand storms. But air on the surface of the ocean does not heat up quickly. Water evaporates from the ocean, cooling the ocean surface and the air, so that the air lingers above the ocean, accumulating more and more water vapor. Eventually, the air will rise, if only because it becomes saturated with water vapor. But we see that water rising from the ocean is not as hot compared to the air above it as is air rising from the desert. The initial rise will be slow compared to the rise over a desert. But if the water starts to condense out of the moist air, and the moist air is surrounded by dry air, the moist air will begin to rise more quickly, sucking more moist air up beneath it.
Thus we expect low-altitude storms over a desert and high-altitude storms over an ocean.
PS. Another writer concludes that the upward force on a cubic yard of air due to condensation will be close to a thousand pounds. He says, "I’m not intending to do the calculations any further here, because it is basic knowledge." Had he performed the calculations, he would have discovered that the effect of water vapor contraction is opposite to his claims (the contraction tends to make the air more dense and therefore sink, while he claimed that the contraction decreases pressure and therefore creates lift) and that his forces were off by four orders of magnitude (the net lift is of order 0.1 pounds per cubic yard, not 700 pounds per cubic yard).
PPS: The debate on this subject continues over at Watt's Up With That?.
PPS. Look in the comments for an explanation of evaporation and condensation on a molecular level.
Consider a kilogram of air that has just been warmed at the surface of the Earth, and is now rising towards the tropopause as part of atmospheric convection. This kilogram has temperature 300 K, pressure 100 kPa, and volume 860 l (liters). Let us suppose this air contains 10 l of water vapor. This water vapor has mass 10 g and would occupy 10 ml (milliliters) if it condensed into liquid.
Our rising volume of air expands and cools. Its pressure drops to 50 kPa and its temperature to 250 K. It expands to 1400 l. At this temperature, almost all of our water must condense into liquid. Before condensation, the water occupies 14 l. When it condenses it will turn into microscopic water droplets that occupy only 14 ml. Of course, these droplets will freeze afterwards, but let's ignore that for now, and consider what happens when the water first condenses.
Most likely, the condensation will occur gradually as the air expands, but we will imagine that it happens after the expansion is complete, so we can calculate the net effect of condensation upon the pressure of our gas. At the end of the expansion, our air contains supersaturated water vapor, like the gas in a cloud chamber.
Consider the first gram of water that condenses. Let us assume, for the time being, that this condensation happens instantly, so that our two cubic meters of air has no time to expand or contract during the process. That is to say: we assume the condensation takes place at constant volume.
Before condensation, this one gram occupied 1.4 l in our volume of 1400 l. After condensation, the water droplets occupy a combined volume of only 1 ml. The remaining air and water vapor expand into our 1400 l. As it expands, its pressure decreases by 0.1%.
When water condenses, it gives up its latent heat of evaporation, which is 2 MJ/kg. When the first gram of water condenses, it gives up 2 kJ of heat to our 1400 l of air. The heat capacity of air at constant volume is roughly 700 kJ/kgK, so our kilogram of air warms up by around 3 K. It's pressure increases by 3 K ÷ 250 K = 1.2%.
We see that the first gram of water condensation causes a net increase in pressure of 1.2% - 0.1% = 1.1% in our kilogram of air. Suppose the air all around is dry. It has not been warmed by condensation. It's pressure has not increased. Our two cubic meters pushes outwards with its greater pressure and expands until it's pressure is the same as that of the surrounding air. It will expand by 1.1%. Its 1 kg of mass will occupy the same volume as 1.011 kg of surrounding dry air. It will experience an upward buoyancy force of 11 g weight, or 0.11 N. This force will cause it to accelerate upwards at 0.11 m/s2. Within less than a minute, it will be traveling upwards at a few meters per second. At that point, other forces will come into play to slow it down. We note that we allowed only 1 g of our water vapor to condense. If all 10 g condensed at once, our kilogram of air would experience ten times more lift.
We see that condensation does indeed cause air to rise more quickly than surrounding dry air.
Moist air will expand more than dry air as it rises towards the tropopause. Evaporation, on the other hand, causes air to rise more slowly. Air at the surface of a dry desert heats up fast in contact with the hot sand. It rises quickly. We get dust devils and sand storms. But air on the surface of the ocean does not heat up quickly. Water evaporates from the ocean, cooling the ocean surface and the air, so that the air lingers above the ocean, accumulating more and more water vapor. Eventually, the air will rise, if only because it becomes saturated with water vapor. But we see that water rising from the ocean is not as hot compared to the air above it as is air rising from the desert. The initial rise will be slow compared to the rise over a desert. But if the water starts to condense out of the moist air, and the moist air is surrounded by dry air, the moist air will begin to rise more quickly, sucking more moist air up beneath it.
Thus we expect low-altitude storms over a desert and high-altitude storms over an ocean.
PS. Another writer concludes that the upward force on a cubic yard of air due to condensation will be close to a thousand pounds. He says, "I’m not intending to do the calculations any further here, because it is basic knowledge." Had he performed the calculations, he would have discovered that the effect of water vapor contraction is opposite to his claims (the contraction tends to make the air more dense and therefore sink, while he claimed that the contraction decreases pressure and therefore creates lift) and that his forces were off by four orders of magnitude (the net lift is of order 0.1 pounds per cubic yard, not 700 pounds per cubic yard).
PPS: The debate on this subject continues over at Watt's Up With That?.
PPS. Look in the comments for an explanation of evaporation and condensation on a molecular level.
Monday, November 8, 2010
Venus
UPDATE: Initial version of this post used diatomic gas equation for the compression of CO2. Have now corrected this oversight, and find that our estimate of Venus's surface temperature is much improved.
One of our readers suggested we consider the atmosphere of Venus. What a good idea. Let's see how well we can estimate Venus's surface temperature using our understanding of atmospheric convection and the greenhouse effect.
According to Wikipedia, Venus's tropopause is at an altitude of 65 km with temperature 243 K (−30°C) and pressure 10 kPa. The surface pressure, meanwhile, is almost a thousand times greater: 9,300 kPa, which is ninety-three times the surface pressure on Earth. Venus's atmosphere is made up almost entirely of CO2, but also contains 150 ppm of SO2 (sulfur dioxide), and this SO2 condenses into liquid droplets so that the atmosphere below the tropopause is filled with pale yellow clouds.
Venus reflects 90% of incident sunlight (it's Bond Albedo is 0.90). The remaining 10% is absorbed. We're not sure what fraction of the Sun's light reaches the surface of Venus, but our guess is 1%. The SO2 clouds refract and reflect light like our own clouds, but SO2 is a pale yellow liquid, not a clear liquid, and will absorb sunlight eventually.
According to Schriver et al., even a 0.5-μm film of SO2 ice will absorb over 20% of long-wave radiation, so a 10-μm droplet of SO2 liquid will absorb it all. The clouds of Venus are near-perfect absorbers of long-wave radiation, and near-perfect radiators too, just like our own water clouds. Unlike the Earth, however, Venus is always entirely covered with clouds. Neither the planet surface nor the lower atmosphere has any opportunity to radiate heat directly into space. Venus radiates heat directly into space only from its cloud-tops and upper atmosphere.
Although most of the sun's heat is reflected back into space, 10% is absorbed, and we estimate that around 1% reaches the surface of the planet. This heat will raise the temperature of the surface until it forces convection. Here is the convection diagram from our Atmospheric Convection post.
Gas warms at the surface. It rises, expands, radiates heat into space, falls, contracts, and warms again. As the gas expands, it gets cooler. As it contracts, it gets warmer. In our simplistic analysis, we assumed that the expansion and contraction were adiabatic, meaning they took place without any heat entering or leaving the gas. In reality, the gas radiates heat to nearby gas, absorbs heat from nearby gas, mixes with nearby gas, and generates heat through viscous friction. But our adiabatic assumption allowed us to estimate the temperature changes using the equation of adiabatic expansion and contraction. For an ideal diatomic gas, such as N2 or O2, p−0.4T1.4 remains constant during adiabatic changes, where p is pressure and T is temperature. For CO2, however, the equation is p−0.3T1.3 at 300 K and p−0.2T1.2 at 1300 K (see here for thermodynamic properties of CO2).
The Earth's tropopause is at altitude 15 km. According to our typical conditions, the tropopause is at 220 K with pressure 22 kPa, while the surface pressure is 100 kPa. Adiabatic compression implies that air descending from the tropopause to the surface will heat up to 340 K. But the Earth's surface is at only 280 K. Air descending 10 km from the tropopause to the surface appears to lose 20% of its heat while contracting to a third of its original volume.
The atmosphere of Venus will heat up as it descends from the tropopause to the surface, and it will be hottest if it does not lose any heat on the way down. The pressure rises from 10 kPa in the tropopause to 9,300 kPa at the surface. The temperature starts at 240 K. Adiabatic compression of an ideal diatomic gas would heat the gas to 1700 K. If we use p−0.25T1.25 as an approximation for CO2, we estimate a final temperature of 941 K.
According to Wikipedia, the surface temperature of Venus is actually 740 K. Carbon dioxide falling 65 km from the tropopause to the surface appears to lose 20% of its heat while being compressed into less than a hundredth of its original volume.
Despite the 20% difference between our calculations and our observations, we see that atmospheric convection makes the surface of Venus incredibly hot while leaving the surface of the Earth delightfully temperate.
If we recall our post on work by convection and another on atmospheric dissipation, we see that a strong convection cycle causes powerful weather. Venus's convection cycle produces an order of magnitude more contraction and expansion than the Earth's. We expect Venus's weather to be an order of magnitude more extreme. And indeed it is.
One of our readers suggested we consider the atmosphere of Venus. What a good idea. Let's see how well we can estimate Venus's surface temperature using our understanding of atmospheric convection and the greenhouse effect.
According to Wikipedia, Venus's tropopause is at an altitude of 65 km with temperature 243 K (−30°C) and pressure 10 kPa. The surface pressure, meanwhile, is almost a thousand times greater: 9,300 kPa, which is ninety-three times the surface pressure on Earth. Venus's atmosphere is made up almost entirely of CO2, but also contains 150 ppm of SO2 (sulfur dioxide), and this SO2 condenses into liquid droplets so that the atmosphere below the tropopause is filled with pale yellow clouds.
Venus reflects 90% of incident sunlight (it's Bond Albedo is 0.90). The remaining 10% is absorbed. We're not sure what fraction of the Sun's light reaches the surface of Venus, but our guess is 1%. The SO2 clouds refract and reflect light like our own clouds, but SO2 is a pale yellow liquid, not a clear liquid, and will absorb sunlight eventually.
According to Schriver et al., even a 0.5-μm film of SO2 ice will absorb over 20% of long-wave radiation, so a 10-μm droplet of SO2 liquid will absorb it all. The clouds of Venus are near-perfect absorbers of long-wave radiation, and near-perfect radiators too, just like our own water clouds. Unlike the Earth, however, Venus is always entirely covered with clouds. Neither the planet surface nor the lower atmosphere has any opportunity to radiate heat directly into space. Venus radiates heat directly into space only from its cloud-tops and upper atmosphere.
Although most of the sun's heat is reflected back into space, 10% is absorbed, and we estimate that around 1% reaches the surface of the planet. This heat will raise the temperature of the surface until it forces convection. Here is the convection diagram from our Atmospheric Convection post.

Gas warms at the surface. It rises, expands, radiates heat into space, falls, contracts, and warms again. As the gas expands, it gets cooler. As it contracts, it gets warmer. In our simplistic analysis, we assumed that the expansion and contraction were adiabatic, meaning they took place without any heat entering or leaving the gas. In reality, the gas radiates heat to nearby gas, absorbs heat from nearby gas, mixes with nearby gas, and generates heat through viscous friction. But our adiabatic assumption allowed us to estimate the temperature changes using the equation of adiabatic expansion and contraction. For an ideal diatomic gas, such as N2 or O2, p−0.4T1.4 remains constant during adiabatic changes, where p is pressure and T is temperature. For CO2, however, the equation is p−0.3T1.3 at 300 K and p−0.2T1.2 at 1300 K (see here for thermodynamic properties of CO2).
The Earth's tropopause is at altitude 15 km. According to our typical conditions, the tropopause is at 220 K with pressure 22 kPa, while the surface pressure is 100 kPa. Adiabatic compression implies that air descending from the tropopause to the surface will heat up to 340 K. But the Earth's surface is at only 280 K. Air descending 10 km from the tropopause to the surface appears to lose 20% of its heat while contracting to a third of its original volume.
The atmosphere of Venus will heat up as it descends from the tropopause to the surface, and it will be hottest if it does not lose any heat on the way down. The pressure rises from 10 kPa in the tropopause to 9,300 kPa at the surface. The temperature starts at 240 K. Adiabatic compression of an ideal diatomic gas would heat the gas to 1700 K. If we use p−0.25T1.25 as an approximation for CO2, we estimate a final temperature of 941 K.
According to Wikipedia, the surface temperature of Venus is actually 740 K. Carbon dioxide falling 65 km from the tropopause to the surface appears to lose 20% of its heat while being compressed into less than a hundredth of its original volume.
Despite the 20% difference between our calculations and our observations, we see that atmospheric convection makes the surface of Venus incredibly hot while leaving the surface of the Earth delightfully temperate.
If we recall our post on work by convection and another on atmospheric dissipation, we see that a strong convection cycle causes powerful weather. Venus's convection cycle produces an order of magnitude more contraction and expansion than the Earth's. We expect Venus's weather to be an order of magnitude more extreme. And indeed it is.
Sunday, October 31, 2010
Self-Regulation by Clouds
On a typical spring day at latitude 30°N, our TEP2 program tells us that the formation of high clouds will tend to warm the Earth's surface by 38°C, while the formation of thick clouds will tend to cool the Earth's surface by 96°C.
Over the past few weeks here in Boston, the warmest days have been those with high, thin clouds, and the coolest have been those with low, thick clouds. But the difference between the warm days and the cold days is only 10°C. Despite alternating clouds, rain, and sunshine, the temperature at a particular location anywhere in the world is almost always within 10°C of its monthly average at mid-day, and these monthly averages vary by less than 1°C from one year to the next.
How can it be that the Earth's surface temperature remains so stable when clouds have such tremendous power to heat and cool the surface? Some kind of self-regulation of cloud formation and evaporation must be taking place. Indeed, at first glance it seems to us that warmth will promote evaporation from the oceans and lead to the formation of the low, thick clouds that cool the Earth, while cold will suppress evaporation, encourage atmospheric convection, and lead to the formation of the high, thin clouds that warm the Earth. So each type of cloud tends to promote the formation of the other, which is a basis for self-regulation.
An example of self-regulation is the action of a thermostat in a house's heating system. When the heater turns on, the house warms up. If the heater stays on, the house will get too hot. The thermostat turns off the heater when the house is warm enough. The house cools down. If the heater stays off, the house will get too cold. The thermostat turns on the heater when the house has cooled enough. The difference between the turn-on and turn-off temperatures is the hysteresis. The temperature half-way between is the set-point.
The heating system in our house can heat the inside to 30°C when the outside is at 0°C. With the heater off, the house will eventually cool to 0°C. But our house is always close to 20°C inside. That's because the set-point of our thermostat is 20°C and its hysteresis is only 1°C.
High clouds at latitude 30°N in spring would heat the Earth to 55°C if the day were long enough and no change to the high clouds took place. Thick clouds would cool the Earth to −79°C. But the mid-day temperature remains within ±5°C of 17°C. The set-point of cloud self-regulation is roughly 17°C and its hysteresis is 10°C. The self-regulation reduces a maximum possible variation of 134°C to an observed variation of 10°C. That's a factor of thirteen reduction through self-regulation.
Our TEP2 program tells us that if we double the CO2 concentration in the atmosphere, the Earth's surface will tend to warm up by 1.5°C. Given the strong self-regulation of warming and cooling by clouds, how much warming will we actually observe if we double the CO2 concentration? It may be that the self-regulation of clouds is entirely independent of the heat retained by extra CO2, so that doubling the CO2 will increase the average temperature of the Earth's surface by a full 1.5°C.
But cloud self-regulation is not independent of the heat absorbed by extra CO2. According to our calculations, doubling the CO2 concentration of the atmosphere causes the atmosphere to retain an additional 5.0 W/m2 of heat. According to our typical atmospheric conditions, air close to the surface contains 1% water vapor, which amounts to roughly 10 g/m3. When this water condenses into water droplets, thus forming a cloud, the water vapor gives up 20 kJ/m3 of latent heat. If this condensation takes place over 1000 s (about fifteen minutes) in a column 1000 m high, it generates 20 kW/m2, which is four thousand times the heat retained by our extra CO2. The heat retained by extra CO2 and the heat produced by condensation are exactly the same type of heat. They are indistinguishable. We think it likely, therefore, that cloud self-regulation will reduce the effect of extra CO2 in the same way that it reduces the effect of cloud variation: by a factor of thirteen. In that case, doubling CO2 concentration will warm up the world by only 0.1°C.
In the presence self-regulation, however, we cannot assume even that CO2 doubling will have a net warming effect. Our calculations show that the extra CO2 causes the heat to be retained mostly between altitudes 3 km and 6 km. In an earlier post we showed how turning on an electric heater in the same room as your home's thermostat will cause the the rest of the house to cool down. It could be that the heat retained by CO2, by virtue of being concentrated in the middle-troposphere, affects cloud self-regulation in such a way as to cause a slight cooling of the surface of the Earth below. Such an outcome seems unlikely, but it is possible.
Another possibility suggested by documents like this one is that the 1.5°C warming from CO2 doubling will in fact be amplified by the self-regulation of clouds, so that we see a 3°C or even 4°C warming due to CO2 doubling. We can think of no examples of such behavior by self-regulating systems, nor do we understand the arguments presented by climatologists who propose such amplification.
In future posts we hope to explore the sources of self-regulation by clouds, and perhaps construct a simple model to investigate how the average temperature of the self-regulated system will be affected by such things as CO2 concentration and the availability of water. Before that, however, we will test our climate model by applying it to day-night variations, and to the planet Venus.
Over the past few weeks here in Boston, the warmest days have been those with high, thin clouds, and the coolest have been those with low, thick clouds. But the difference between the warm days and the cold days is only 10°C. Despite alternating clouds, rain, and sunshine, the temperature at a particular location anywhere in the world is almost always within 10°C of its monthly average at mid-day, and these monthly averages vary by less than 1°C from one year to the next.
How can it be that the Earth's surface temperature remains so stable when clouds have such tremendous power to heat and cool the surface? Some kind of self-regulation of cloud formation and evaporation must be taking place. Indeed, at first glance it seems to us that warmth will promote evaporation from the oceans and lead to the formation of the low, thick clouds that cool the Earth, while cold will suppress evaporation, encourage atmospheric convection, and lead to the formation of the high, thin clouds that warm the Earth. So each type of cloud tends to promote the formation of the other, which is a basis for self-regulation.
An example of self-regulation is the action of a thermostat in a house's heating system. When the heater turns on, the house warms up. If the heater stays on, the house will get too hot. The thermostat turns off the heater when the house is warm enough. The house cools down. If the heater stays off, the house will get too cold. The thermostat turns on the heater when the house has cooled enough. The difference between the turn-on and turn-off temperatures is the hysteresis. The temperature half-way between is the set-point.
The heating system in our house can heat the inside to 30°C when the outside is at 0°C. With the heater off, the house will eventually cool to 0°C. But our house is always close to 20°C inside. That's because the set-point of our thermostat is 20°C and its hysteresis is only 1°C.
High clouds at latitude 30°N in spring would heat the Earth to 55°C if the day were long enough and no change to the high clouds took place. Thick clouds would cool the Earth to −79°C. But the mid-day temperature remains within ±5°C of 17°C. The set-point of cloud self-regulation is roughly 17°C and its hysteresis is 10°C. The self-regulation reduces a maximum possible variation of 134°C to an observed variation of 10°C. That's a factor of thirteen reduction through self-regulation.
Our TEP2 program tells us that if we double the CO2 concentration in the atmosphere, the Earth's surface will tend to warm up by 1.5°C. Given the strong self-regulation of warming and cooling by clouds, how much warming will we actually observe if we double the CO2 concentration? It may be that the self-regulation of clouds is entirely independent of the heat retained by extra CO2, so that doubling the CO2 will increase the average temperature of the Earth's surface by a full 1.5°C.
But cloud self-regulation is not independent of the heat absorbed by extra CO2. According to our calculations, doubling the CO2 concentration of the atmosphere causes the atmosphere to retain an additional 5.0 W/m2 of heat. According to our typical atmospheric conditions, air close to the surface contains 1% water vapor, which amounts to roughly 10 g/m3. When this water condenses into water droplets, thus forming a cloud, the water vapor gives up 20 kJ/m3 of latent heat. If this condensation takes place over 1000 s (about fifteen minutes) in a column 1000 m high, it generates 20 kW/m2, which is four thousand times the heat retained by our extra CO2. The heat retained by extra CO2 and the heat produced by condensation are exactly the same type of heat. They are indistinguishable. We think it likely, therefore, that cloud self-regulation will reduce the effect of extra CO2 in the same way that it reduces the effect of cloud variation: by a factor of thirteen. In that case, doubling CO2 concentration will warm up the world by only 0.1°C.
In the presence self-regulation, however, we cannot assume even that CO2 doubling will have a net warming effect. Our calculations show that the extra CO2 causes the heat to be retained mostly between altitudes 3 km and 6 km. In an earlier post we showed how turning on an electric heater in the same room as your home's thermostat will cause the the rest of the house to cool down. It could be that the heat retained by CO2, by virtue of being concentrated in the middle-troposphere, affects cloud self-regulation in such a way as to cause a slight cooling of the surface of the Earth below. Such an outcome seems unlikely, but it is possible.
Another possibility suggested by documents like this one is that the 1.5°C warming from CO2 doubling will in fact be amplified by the self-regulation of clouds, so that we see a 3°C or even 4°C warming due to CO2 doubling. We can think of no examples of such behavior by self-regulating systems, nor do we understand the arguments presented by climatologists who propose such amplification.
In future posts we hope to explore the sources of self-regulation by clouds, and perhaps construct a simple model to investigate how the average temperature of the self-regulated system will be affected by such things as CO2 concentration and the availability of water. Before that, however, we will test our climate model by applying it to day-night variations, and to the planet Venus.
Labels:
Climate Models,
CO2,
Greenhouse Effect,
Weather
Tuesday, October 26, 2010
Thick Clouds
We have been using our computer program, TEP2 to estimate how much the Earth's surface will tend to warm up if we make certain permanent changes to its atmosphere. In With 660 ppm CO2 we found that doubling the atmosphere's CO2 concentration from 330 ppm to 660 ppm tends to warm the Earth's surface by 1.5°C. In High Clouds we found that the formation of high, thin clouds in a clear sky will tend to warm the Earth's surface by 38°C.
Today we consider the effect of thick clouds. We start with the Earth on a typical clear spring day at latitude 30°N, as represented by our EA1.txt absorption spectra. Our TEP2 program tells us that the total escaping power is 252.5 W/m2. We allow a thick cloud to form from altitude 3 km to 12 km. In Clouds we argued that a cloud this thick will reflect 90% of the Sun's radiation and absorb 100% of the Earth's radiation. We simulate such a cloud by setting the absorption of our 3-km, 6-km, and 9-km layers to 1.0 for wavelengths 5 μm to 60 μm to produce EA4. We apply TEP2 to EA4 and obtain the following output.
As we did in High Clouds, let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. The total power escaping the earth is 252.5 W/m2, so the total power arriving from the Sun must be 252.5 W/m2 also. In the conditions described by EA4, 90% of the heat arriving from the Sun is reflected back into space, so only 25.2 W/m2 is absorbed by the Earth. But the total power escaping the Earth is 136.5 W/m2. When these large clouds form, the Earth will start to radiate 111 W/m2 more than it absorbs. It will cool down. In our TEP2 program, we decrease the temperature of the Earth and its atmosphere until we arrive at the following output.
According to our simulation, the formation of a 9-km thick layer of cloud at altitude 3 km has a cooling effect sixty-four times stronger than the warming effect of doubling the atmosphere's CO2 concentration.
UPDATE: When we look at discussions like this one about clouds, we see that climatologists recognize the power of clouds to cool and warm the Earth. But we don't see them giving us values in Centigrade in the same way that they do for a hypothetical doubling of CO2 concentration.
Today we consider the effect of thick clouds. We start with the Earth on a typical clear spring day at latitude 30°N, as represented by our EA1.txt absorption spectra. Our TEP2 program tells us that the total escaping power is 252.5 W/m2. We allow a thick cloud to form from altitude 3 km to 12 km. In Clouds we argued that a cloud this thick will reflect 90% of the Sun's radiation and absorb 100% of the Earth's radiation. We simulate such a cloud by setting the absorption of our 3-km, 6-km, and 9-km layers to 1.0 for wavelengths 5 μm to 60 μm to produce EA4. We apply TEP2 to EA4 and obtain the following output.
------------------------------------------------This output is exactly the same as the one we obtained for high clouds. Both the high clouds and the thick clouds have the same effect upon the total escaping heat. The difference between high clouds and thick clouds is that thick clouds block 90% of the Sun's heat from reaching the Earth, while high clouds block only 10%.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 388.8 0.0
0-km 280.0 348.5 262.6 0.0
3-km 270.0 301.3 292.0 0.0
6-km 250.0 221.5 214.0 0.0
9-km 230.0 158.7 152.3 120.8
12-km 220.0 132.8 22.2 10.1
15-km 220.0 132.8 14.4 5.5
------------------------------------------------
Total: 136.5
------------------------------------------------
As we did in High Clouds, let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. The total power escaping the earth is 252.5 W/m2, so the total power arriving from the Sun must be 252.5 W/m2 also. In the conditions described by EA4, 90% of the heat arriving from the Sun is reflected back into space, so only 25.2 W/m2 is absorbed by the Earth. But the total power escaping the Earth is 136.5 W/m2. When these large clouds form, the Earth will start to radiate 111 W/m2 more than it absorbs. It will cool down. In our TEP2 program, we decrease the temperature of the Earth and its atmosphere until we arrive at the following output.
------------------------------------------------Here we see the total escaping heat is 26.3 W/m2, which is pretty close to the 25.2 W/m2 arriving from the Sun through the thick clouds. The Earth's surface has cooled by 96°C.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 194.3 80.8 76.0 0.0
0-km 187.6 70.2 59.0 0.0
3-km 180.9 60.7 56.4 0.0
6-km 167.5 44.6 40.8 0.0
9-km 154.1 32.0 28.7 22.3
12-km 147.4 26.8 4.5 2.9
15-km 147.4 26.8 2.1 1.1
------------------------------------------------
Total: 26.3
------------------------------------------------
According to our simulation, the formation of a 9-km thick layer of cloud at altitude 3 km has a cooling effect sixty-four times stronger than the warming effect of doubling the atmosphere's CO2 concentration.
UPDATE: When we look at discussions like this one about clouds, we see that climatologists recognize the power of clouds to cool and warm the Earth. But we don't see them giving us values in Centigrade in the same way that they do for a hypothetical doubling of CO2 concentration.
Monday, October 18, 2010
High Clouds
Sitting on a plane over the Atlantic Ocean last month, I was at 13,000 m looking down on a continuous layer of thin, high cloud. Through occasional openings, the ocean below appeared brightly-lit despite the clouds above it. Today we estimate the effect of such a cloud layer upon total escaping power using our TEP2 program.
Let us place a 1-km thick layer of cloud in our 9-km atmospheric layer. This layer extends from altitude 9 km to 12 km. In our previous post we showed that a 1-km thick layer of cloud absorbs 100% of incident long-wave radiation, but only 10% of incident short-wave radiation. In our atmospheric absorption spectra we simulate such a cloud by setting the absorption of our 9-km layer to 1.0 for wavelengths 5 μm to 60 μm. We start with our EA1 spectra (typical, clear, spring day at 30°N) and produce EA3. We submit EA3 to TEP2 and obtain the following table of escaping power in W/m2. We add the final column by hand, which gives the change in escaping power caused by the introduction of the cloud.
We note that the black-body radiation for our 9-km layer is 158.7 W/m2 (BB column) while the heat that TEP2 calculates by numerical integration is only 152.3 W/m2 (Layer column). Our spectra extend to 60 μm, but the cool cloud (−43°C) radiates some power in the range 60-100 μm. We will accept this 4% error and move on.
The cloud causes the total escaping power to drop by 116 W/m2, or 46%. We now ask how much warmer the Earth's surface will have to get in order to make up a 46% drop in total escaping power caused by the formation of a 1-km layer of cloud at altitude 10 km. The 1-km cloud absorbs some of the heat arriving from the Sun, and we must take this into account somehow when we perform our estimate.
Let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. Because the Earth and its atmosphere radiate a total of of 252.5 W/m2, we suppose that a like amount of heat arrives from the Sun and lands upon the Earth's surface. When we place a 1-km layer of cloud in the way, we estimate that 10% of the Sun's heat will be reflected back out into space. When the cloud layer forms, the heat arriving from the Sun decreases to 227 W/m2 and the heat escaping from the Earth decreases to 136 W/m2.
By experimenting with TEP2, we find that a 13% increase in the absolute temperature of the Earth and its atmospheric layers will produce the following result.
According to our simulation, the formation of a 1-km thick layer of cloud at altitude 10 km has twenty-five times the warming effect as doubling the atmosphere's CO2 concentration.
UPDATE: Michele points out that high clouds will contain microscopic ice particles instead of water droplets. Ice, like water, is also opaque to long-wave radiation and transparent to short-wave radiation.
Let us place a 1-km thick layer of cloud in our 9-km atmospheric layer. This layer extends from altitude 9 km to 12 km. In our previous post we showed that a 1-km thick layer of cloud absorbs 100% of incident long-wave radiation, but only 10% of incident short-wave radiation. In our atmospheric absorption spectra we simulate such a cloud by setting the absorption of our 9-km layer to 1.0 for wavelengths 5 μm to 60 μm. We start with our EA1 spectra (typical, clear, spring day at 30°N) and produce EA3. We submit EA3 to TEP2 and obtain the following table of escaping power in W/m2. We add the final column by hand, which gives the change in escaping power caused by the introduction of the cloud.
-------------------------------------------------------No radiation escapes into space from the Earth's surface or from the first three layers of the atmosphere. A total of 210.4 W/m2 is absorbed by the lower surface of the cloud layer. The cloud layer itself, however, is a fine radiator of heat, and radiates 120.8 W/m2 into space.
Name Temp BB Layer Escaping Change
-------------------------------------------------------
Surface 290.0 401.1 388.8 0.0 -80.0
0-km 280.0 348.5 262.6 0.0 -46.1
3-km 270.0 301.3 184.8 0.0 -39.7
6-km 250.0 221.5 111.5 0.0 -44.6
9-km 230.0 158.7 152.3 120.8 94.4
12-km 220.0 132.8 22.2 10.1 0.0
15-km 220.0 132.8 14.4 5.5 0.0
-------------------------------------------------------
Total: 136.5 -116.0
-------------------------------------------------------
We note that the black-body radiation for our 9-km layer is 158.7 W/m2 (BB column) while the heat that TEP2 calculates by numerical integration is only 152.3 W/m2 (Layer column). Our spectra extend to 60 μm, but the cool cloud (−43°C) radiates some power in the range 60-100 μm. We will accept this 4% error and move on.
The cloud causes the total escaping power to drop by 116 W/m2, or 46%. We now ask how much warmer the Earth's surface will have to get in order to make up a 46% drop in total escaping power caused by the formation of a 1-km layer of cloud at altitude 10 km. The 1-km cloud absorbs some of the heat arriving from the Sun, and we must take this into account somehow when we perform our estimate.
Let us suppose that the Earth radiates as much heat as it absorbs when its surface and atmosphere are as described by EA1. Because the Earth and its atmosphere radiate a total of of 252.5 W/m2, we suppose that a like amount of heat arrives from the Sun and lands upon the Earth's surface. When we place a 1-km layer of cloud in the way, we estimate that 10% of the Sun's heat will be reflected back out into space. When the cloud layer forms, the heat arriving from the Sun decreases to 227 W/m2 and the heat escaping from the Earth decreases to 136 W/m2.
By experimenting with TEP2, we find that a 13% increase in the absolute temperature of the Earth and its atmospheric layers will produce the following result.
------------------------------------------------The total escaping power is now 225 W/m2, which is close enough to the 227 W/m2 arriving from the Sun. When a cloud forms at altitude 10 km, the heat escaping from the Earth will balance that arriving from the Sun only if the Earth's surface warms by 38°C. If, instead of a cloud forming at 10 km, we double the CO2 concentration from 330 ppm to 660 ppm, the same calculation suggests the Earth will warm by only 1.5°C.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 327.7 653.9 629.9 0.0
0-km 316.4 568.3 413.4 0.0
3-km 305.1 491.3 284.7 0.0
6-km 282.5 361.1 169.3 0.0
9-km 259.9 258.7 250.4 201.4
12-km 248.6 216.6 34.6 14.8
15-km 248.6 216.6 23.5 8.7
------------------------------------------------
Total: 224.9
------------------------------------------------
According to our simulation, the formation of a 1-km thick layer of cloud at altitude 10 km has twenty-five times the warming effect as doubling the atmosphere's CO2 concentration.
UPDATE: Michele points out that high clouds will contain microscopic ice particles instead of water droplets. Ice, like water, is also opaque to long-wave radiation and transparent to short-wave radiation.
Thursday, October 14, 2010
Clouds
Clouds contain microscopic droplets of water. The droplets are around 10 μm in diameter and there are hundreds of them in every cubic centimeter (see here). We discussed the absorption of long-wave radiation by water in an earlier post. We presented a graph of water's absorption length versus radiation wavelength. The graph shows that the absorption length for 5 μm to 60 μm radiation is less than 20 μm. A 100-μm layer of water will absorb 99% of long-wave radiation.
Let us consider the fate of a single long-wave photon as it enters a cloud. The photon may pass all the way through the first centimeter of the cloud without touching a single droplet, or it might strike a droplet. If we assume our droplets have cross-section 100 μm2, the chance of our photon striking any particular droplet while passing through the first cubic centimeter is one in a million. The chance of the photon striking any one of a hundred droplets in the same cubic centimeter is a hundred times greater, or one in ten thousand. In every 100 m of cloud, the expected number of droplets our photon will strike is one (that's one in ten thousand per centimeter times ten thousand centimeters).
When the photon strikes a droplet, it can reflect off the surface or it can enter the liquid. According to this graph from Querry et al., the reflectance of water to long-wave radiation is 2% when the photon approaches at 10° to the perpendicular, 10% at 60°, 20% at 70° and 80% at 87°. The chance of a long-wave photon reflecting from a random spot on the surface of a droplet is around 10%. We also note that most reflection takes place when the photon strikes the droplet at a small angle to the surface, so the photon will continue into the cloud after reflection.
If a photon enters a 10-μm droplet, it will pass through something like 10 μm of water and strike the opposite, inner surface. Here it might reflect back into the droplet. But let's keep things simple: if the photon strikes a droplet, it will most likely enter the droplet, pass through 10 μm of water and keep going.
With 100 droplets in each cubic centimeter, our photon must pass through one droplet on average for each hundred meters of cloud. In 1 km of cloud, our photon will pass through ten droplets. In order to pass through the cloud, it will have to pass through roughly 100 μm of water. But we know that 100 μm of water absorbs 99% of all long-wave radiation. So a 1-km cloud is opaque to long-wave radiation.
Clouds have a different effect upon short-wave radiation, such as sunlight. Short-wave radiation reflects off the air-water surface far more readily than long-wave radiation, and once inside, it is more likely to reflect off the internal surface as well (internal reflection within droplets is what causes rainbows). But on the other hand, the absorption length of visible light in water is tens of meters. The water in a thick cloud will not absorb short-wave radiation. Instead, short-wave radiation changes direction as it encounters water droplets. It can change direction by reflecting off the outer or inner surface of a droplet. It can change direction by refraction as it enters or leaves a droplet. The reason thick clouds are dark is because sunlight is being turned around and re-directed back into space by the cloud's water droplets, not because sunlight is being absorbed by the clouds.
A short-wave photon passing through 1 km of cloud will encounter only ten droplets. These ten droplets are enough to absorb long-wave radiation, but they are not enough to guarantee that the short-wave photon gets re-directed back out of the cloud. With the help of some pencil drawings, we estimate that it would require encounters with one hundred droplets to guarantee that the photon came back out of the cloud on the same side that it went in. A 1-km thick cloud might reflect 10% of the short-wave radiation incident upon it, while a 10-km thick cloud will reflect 90%.
A 1-km layer of cloud acts like a black-body absorber of long-wave radiation. By radiative symmetry, this same 1-km layer must also be a perfect black-body radiator of long-wave radiation. We estimate that this same 1-km of cloud will allow 90% of short-wave radiation to pass through, while reflecting 10%. A 10-km layer of cloud, meanwhile, will allow only 10% of short-wave radiation to pass through, while reflecting 90%.
Heat radiated by the Earth will be absorbed by clouds. These same clouds will radiate their own heat out into space. Sunlight will be reflected off their top surfaces. In our next post, we will consider the effect of a 1-km layer of cloud at altitude 10 km upon the Earth's total escaping power and upon the amount of heat arriving from the Sun.
UPDATE: Cirrus clouds appear to be examples of our 1-km cloud layer. According to NASA, cirrus clouds are opaque to long-wave radiation, but largely transparent to short-wave radiation.
UPDATE: We see here confirmation of our estimates: clouds reflect from 10% to over 90% of short-wave radiation (albedo is 0.1 to over 0.9).
Let us consider the fate of a single long-wave photon as it enters a cloud. The photon may pass all the way through the first centimeter of the cloud without touching a single droplet, or it might strike a droplet. If we assume our droplets have cross-section 100 μm2, the chance of our photon striking any particular droplet while passing through the first cubic centimeter is one in a million. The chance of the photon striking any one of a hundred droplets in the same cubic centimeter is a hundred times greater, or one in ten thousand. In every 100 m of cloud, the expected number of droplets our photon will strike is one (that's one in ten thousand per centimeter times ten thousand centimeters).
When the photon strikes a droplet, it can reflect off the surface or it can enter the liquid. According to this graph from Querry et al., the reflectance of water to long-wave radiation is 2% when the photon approaches at 10° to the perpendicular, 10% at 60°, 20% at 70° and 80% at 87°. The chance of a long-wave photon reflecting from a random spot on the surface of a droplet is around 10%. We also note that most reflection takes place when the photon strikes the droplet at a small angle to the surface, so the photon will continue into the cloud after reflection.
If a photon enters a 10-μm droplet, it will pass through something like 10 μm of water and strike the opposite, inner surface. Here it might reflect back into the droplet. But let's keep things simple: if the photon strikes a droplet, it will most likely enter the droplet, pass through 10 μm of water and keep going.
With 100 droplets in each cubic centimeter, our photon must pass through one droplet on average for each hundred meters of cloud. In 1 km of cloud, our photon will pass through ten droplets. In order to pass through the cloud, it will have to pass through roughly 100 μm of water. But we know that 100 μm of water absorbs 99% of all long-wave radiation. So a 1-km cloud is opaque to long-wave radiation.
Clouds have a different effect upon short-wave radiation, such as sunlight. Short-wave radiation reflects off the air-water surface far more readily than long-wave radiation, and once inside, it is more likely to reflect off the internal surface as well (internal reflection within droplets is what causes rainbows). But on the other hand, the absorption length of visible light in water is tens of meters. The water in a thick cloud will not absorb short-wave radiation. Instead, short-wave radiation changes direction as it encounters water droplets. It can change direction by reflecting off the outer or inner surface of a droplet. It can change direction by refraction as it enters or leaves a droplet. The reason thick clouds are dark is because sunlight is being turned around and re-directed back into space by the cloud's water droplets, not because sunlight is being absorbed by the clouds.
A short-wave photon passing through 1 km of cloud will encounter only ten droplets. These ten droplets are enough to absorb long-wave radiation, but they are not enough to guarantee that the short-wave photon gets re-directed back out of the cloud. With the help of some pencil drawings, we estimate that it would require encounters with one hundred droplets to guarantee that the photon came back out of the cloud on the same side that it went in. A 1-km thick cloud might reflect 10% of the short-wave radiation incident upon it, while a 10-km thick cloud will reflect 90%.
A 1-km layer of cloud acts like a black-body absorber of long-wave radiation. By radiative symmetry, this same 1-km layer must also be a perfect black-body radiator of long-wave radiation. We estimate that this same 1-km of cloud will allow 90% of short-wave radiation to pass through, while reflecting 10%. A 10-km layer of cloud, meanwhile, will allow only 10% of short-wave radiation to pass through, while reflecting 90%.
Heat radiated by the Earth will be absorbed by clouds. These same clouds will radiate their own heat out into space. Sunlight will be reflected off their top surfaces. In our next post, we will consider the effect of a 1-km layer of cloud at altitude 10 km upon the Earth's total escaping power and upon the amount of heat arriving from the Sun.
UPDATE: Cirrus clouds appear to be examples of our 1-km cloud layer. According to NASA, cirrus clouds are opaque to long-wave radiation, but largely transparent to short-wave radiation.
UPDATE: We see here confirmation of our estimates: clouds reflect from 10% to over 90% of short-wave radiation (albedo is 0.1 to over 0.9).
Thursday, October 7, 2010
Absorption By All Higher Layers
Our Total Escaping Power program calculates the total power radiated by the Earth and its atmosphere given the absorption spectra of a sequence of atmospheric layers. The program does not dictate the thickness of these layers, nor even do the layers have to have the same thickness, but we did assume that radiation passing through one layer will be certain to pass through all higher layers. If we want to experiment with greater water vapor content in an upper layer, or if we want to include a layer of clouds, we will need a program that does not rely upon this assumption.
We modified our TEP1 program to produce TEP2. The new program applies the absorption of all higher layers to upward radiation. The result is a decrease in total escaping power. Here is the output of the new program when we apply it to our EA1 spectra, which assume 330 ppm CO2. We have added by hand a final column giving the change in escaping power caused by applying the absorption of all upper layers.
The enhancement of our model makes only a slight change in our CO2 doubling temperature, but it allows us to include upper layers that are more absorbent than lower layers. We can look forward to including layers of clouds and layers of excess humidity, and seeing how they effect the total escaping power.
We modified our TEP1 program to produce TEP2. The new program applies the absorption of all higher layers to upward radiation. The result is a decrease in total escaping power. Here is the output of the new program when we apply it to our EA1 spectra, which assume 330 ppm CO2. We have added by hand a final column giving the change in escaping power caused by applying the absorption of all upper layers.
---------------------------------------------------------In our discussion of TEP1, we claimed that our assumption of upper transparency would cause less than a 10% error in our calculation of total escaping power. It turns out that including the absorption of upper layers causes a 15% drop. Let's apply TEP1 to our EA2 spectra, which assume 660 ppm CO2.
Name Temp BB Layer Escaping Change
---------------------------------------------------------
Surface 290.0 401.1 388.8 80.0 -9.8
0-km 280.0 348.5 262.6 46.1 -12.8
3-km 270.0 301.3 184.8 39.7 -10.0
6-km 250.0 221.5 111.5 44.6 -6.8
9-km 230.0 158.7 50.7 26.4 -3.0
12-km 220.0 132.8 22.2 10.1 -1.1
15-km 220.0 132.8 14.4 5.5 -0.0
---------------------------------------------------------
Total: 252.5 -43.5
---------------------------------------------------------
------------------------------------------------We see a 5 W/m2 decrease in total escaping power due to doubling the CO2 concentration from 330 ppm to 660 ppm. The drop is 2.0%, slightly less than the 2.2% calculated by TEP1. If we repeat our calculation of CO2 doubling temperature using TEP2, we arrive at a value of 1.5°C, slightly less than the 1.6°C calculated by TEP1.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 388.8 78.8
0-km 280.0 348.5 264.0 44.2
3-km 270.0 301.3 188.6 38.2
6-km 250.0 221.5 115.2 43.9
9-km 230.0 158.7 53.4 26.4
12-km 220.0 132.8 24.2 10.3
15-km 220.0 132.8 16.3 5.7
------------------------------------------------
Total: 247.5
------------------------------------------------
The enhancement of our model makes only a slight change in our CO2 doubling temperature, but it allows us to include upper layers that are more absorbent than lower layers. We can look forward to including layers of clouds and layers of excess humidity, and seeing how they effect the total escaping power.
Wednesday, October 6, 2010
With 660 ppm CO2
In our In our previous post we extended our atmospheric absorption spectra to cover wavelengths 5 μm to 60 μm. These spectra assume CO2 concentration 330 ppm, which is typical for the Earth today, and temperature and water vapor concentration typical for a 30°N on a clear spring day. We plotted the extended spectra and applied them as input to our total escaping power program. The program says that the total power radiated by the Earth's surface and its atmosphere below the tropopause is 296.0 W.
Today we make one change to our atmospheric conditions: we double the CO2 concentration to 660 ppm. We leave water vapor concentration, temperature, and pressure the same. With the help of the Spectral Calculator, we obtain new absorption spectra and plot them.
We feed our new spectra into our total escaping power program, and obtain the following output. The final column we added by hand. It gives us the change in total escaping power when we raise CO2 concentration from 330 ppm to 660 ppm.
According to Stephan's Law, the amount of power radiated by a black body increases as the fourth power of its temperature. For small changes in temperature, the amount of power radiated by any body will increase as the fourth power of its temperature. A 1% increase in temperature will cause a 4% increase in radiated power. In order to increase total escaping power by 2.2%, we can increase the temperature of the Earth's surface and all the atmospheric layers by one quarter of 2.2%, or 0.55%. We increased all our layer temperatures by 0.55% and applied our total escaping power program to the resulting atmospheric layers. We obtain the following output. Note that the new temperatures are recorded in the first column.
Our analysis considered only the heat radiated by the troposphere, which is the region of the atmosphere below the tropopause. We ignored the effect of increased CO2 upon the stratosphere, which is the region above the tropopause. Even though there is no net heat flow between the troposphere and the stratosphere, an overall warming or cooling of the stratosphere will affect the temperature of the troposphere, and therefore change its total radiated power. Furthermore, we ignored the effect of increased CO2 upon radiation arriving from the Sun. We will consider these effects in future posts. In our next post, however, we will try doubling the water vapor concentration in various atmospheric layers and re-calculating total escaping power. By this means, we will be able to determine whether the effect of CO2 upon total escaping power is significant compared that of water vapor.
UPDATE: See slightly improved calculation of CO2 warming in next post, where we arrive at 1.5°C instead of 1.6°C as the size of the effect.
Today we make one change to our atmospheric conditions: we double the CO2 concentration to 660 ppm. We leave water vapor concentration, temperature, and pressure the same. With the help of the Spectral Calculator, we obtain new absorption spectra and plot them.

We feed our new spectra into our total escaping power program, and obtain the following output. The final column we added by hand. It gives us the change in total escaping power when we raise CO2 concentration from 330 ppm to 660 ppm.
-------------------------------------------------------The total escaping power drops by 6.6 W/m2. The power escaping from the Earth's surface and the first three 3-km layers of the atmosphere decreases by 7.2 W/m2, but the power radiated by the top three layers increases by 0.8 W/m2. In the lower layers, more CO2 causes more radiation to be absorbed on its way into space. In the upper layers, more CO2 allows the atmosphere to radiate its heat more efficiently into space. We see that the increased absorption far outweighs the increased radiation, and the result is a 2.2% reduction in the heat escaping the Earth.
Name Temp BB Layer Escaping Change
-------------------------------------------------------
Surface 290.0 401.1 388.8 88.2 -1.6
0-km 280.0 348.5 264.0 55.6 -3.3
3-km 270.0 301.3 188.6 47.8 -1.9
6-km 250.0 221.5 115.2 51.0 -0.4
9-km 230.0 158.7 53.4 29.7 +0.3
12-km 220.0 132.8 24.2 11.5 +0.3
15-km 220.0 132.8 16.3 5.7 +0.2
-------------------------------------------------------
Total: 289.4 -6.6
-------------------------------------------------------
According to Stephan's Law, the amount of power radiated by a black body increases as the fourth power of its temperature. For small changes in temperature, the amount of power radiated by any body will increase as the fourth power of its temperature. A 1% increase in temperature will cause a 4% increase in radiated power. In order to increase total escaping power by 2.2%, we can increase the temperature of the Earth's surface and all the atmospheric layers by one quarter of 2.2%, or 0.55%. We increased all our layer temperatures by 0.55% and applied our total escaping power program to the resulting atmospheric layers. We obtain the following output. Note that the new temperatures are recorded in the first column.
------------------------------------------------We see that there is no net change in total radiated power when we combine a doubling of CO2 concentration with a 1.6°C warming of the Earth's surface. That's not to say that the Earth will actually warm up by 1.6°C if we double the CO2 concentration, because the climate might be a chaotic system that defies such simple logic, or a system with feedback that acts in quite the opposite manner to our expectations. Nevertheless, in the absence of such complex behavior, the doubling the CO2 concentration will tend to warm the Earth by 1.6°C. This 1.6°C is our estimate of the Earth's CO2 doubling temperature.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 291.6 410.0 397.5 90.6
0-km 281.5 356.1 269.3 57.0
3-km 271.5 308.1 192.3 48.8
6-km 251.4 226.5 117.4 52.0
9-km 231.3 162.3 54.4 30.2
12-km 221.2 135.8 24.7 11.7
15-km 221.2 135.8 16.7 5.9
------------------------------------------------
Total: 296.1
------------------------------------------------
Our analysis considered only the heat radiated by the troposphere, which is the region of the atmosphere below the tropopause. We ignored the effect of increased CO2 upon the stratosphere, which is the region above the tropopause. Even though there is no net heat flow between the troposphere and the stratosphere, an overall warming or cooling of the stratosphere will affect the temperature of the troposphere, and therefore change its total radiated power. Furthermore, we ignored the effect of increased CO2 upon radiation arriving from the Sun. We will consider these effects in future posts. In our next post, however, we will try doubling the water vapor concentration in various atmospheric layers and re-calculating total escaping power. By this means, we will be able to determine whether the effect of CO2 upon total escaping power is significant compared that of water vapor.
UPDATE: See slightly improved calculation of CO2 warming in next post, where we arrive at 1.5°C instead of 1.6°C as the size of the effect.
Wednesday, September 29, 2010
Extended Atmospheric Absorption Spectra
In our previous post we concluded that we needed to extend our existing absorption spectra to cover the range 5 μm to 60 μm. So we returned to the Spectral Calculator and, entered our gas properties for each atmospheric layer, and obtained the absorption spectra from 30 μm to 60 μm. We added these to our existing spectra and obtained the following graph (click for a larger version).
As a point of detail, each spectrum we receive from the Spectral Calculator contain tens of thousands of values. We condense the spectra using a program that calculates the average absorption in each 0.1-μm window. The result is a spectrum with a point every tenth of a micron. You will find the original spectra in our data archive, in the EA_1 folder. You will find the condensed spectra here. The condensed file can act as input to our climate models and is convenient for generating plots like the one above.
We apply our total escaping power program to our extended spectra and obtain the following values for power per square meter. For an explanation of the various columns, see here.
We experiment with the black-body radiation spectrum using this program. When we integrate in 0.1-μm steps all the way from 1 μm to 300 μm, we get a total power of 401.0 W/m2, which is almost exactly what we obtain from Stefan's Law. We use our program to determine the power radiated by a black body at various wavelengths.
Our next step is to generate a new set of spectra for the atmosphere with 660 ppm CO2, and see how the total escaping power changes. Our guess is that the total escaping power will decrease, but we are not sure by how much.

As a point of detail, each spectrum we receive from the Spectral Calculator contain tens of thousands of values. We condense the spectra using a program that calculates the average absorption in each 0.1-μm window. The result is a spectrum with a point every tenth of a micron. You will find the original spectra in our data archive, in the EA_1 folder. You will find the condensed spectra here. The condensed file can act as input to our climate models and is convenient for generating plots like the one above.
We apply our total escaping power program to our extended spectra and obtain the following values for power per square meter. For an explanation of the various columns, see here.
------------------------------------------------Let's look at the first line of numbers, which apply to the surface of the Earth. We treat the surface as a black body, as we justify elsewhere. Using Stefan's Law we find that a black body at 290 K (that's 17°C) should radiate 401.1 W/m2. Our calculator adds the power radiated in each 0.1-μm window from 5 μm to 60 μm, in a process we call numerical integration, and arrives at 388.8 W/m2. That's closer to 401.1 W/m2 than the 349.0 W/m2 we obtained when we our calculation extended only to 30 μm. But we still have a difference of 12.3 W/m2.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 388.8 89.8
0-km 280.0 348.5 262.6 58.9
3-km 270.0 301.3 184.8 49.7
6-km 250.0 221.5 111.5 51.4
9-km 230.0 158.7 50.7 29.4
12-km 220.0 132.8 22.2 11.2
15-km 220.0 132.8 14.4 5.5
------------------------------------------------
Total: 296.0
------------------------------------------------
We experiment with the black-body radiation spectrum using this program. When we integrate in 0.1-μm steps all the way from 1 μm to 300 μm, we get a total power of 401.0 W/m2, which is almost exactly what we obtain from Stefan's Law. We use our program to determine the power radiated by a black body at various wavelengths.
--------------------------We have a total of 12.2 W outside the 5-60 μm range of our absorption spectra. In the future, perhaps we will extend our spectra to include this missing 3%, but for now we are content with our omission. Furthermore, we are satisfied that our numerical integration in 0.1-μm steps, which is the basis of our climate model's calculations, is accurate to better than 0.1%.
Range (um) Power (W/m^2)
--------------------------
0.1-1 0.0
1-5 3.8
5-60 388.8
60-100 6.4
100-200 1.8
200-300 0.2
--------------------------
Total 401.0
--------------------------
Our next step is to generate a new set of spectra for the atmosphere with 660 ppm CO2, and see how the total escaping power changes. Our guess is that the total escaping power will decrease, but we are not sure by how much.
Wednesday, September 22, 2010
Total Escaping Power
Our current approach to modeling the Earth's greenhouse effect is to divide the Earth's atmosphere in to 3-km layers. So far, we have considered how each of the first seven layers absorbs and emits long-wave radiation. Our study of these seven layers has been motivated by a desire to calculate the total heat radiated into space by the Earth and its atmosphere, and ultimately to estimate the strength of the relationship between the Earth's surface temperature and the concentration of CO2 in its atmosphere.
In previous posts, we simplified our discussion by assuming that each atmospheric layer was either perfectly transparent or absolutely opaque at each wavelength. This assumption, combined with an examination of the absorption spectra, allowed us to say that all radiation passing through one layer would be sure to pass through all higher layers as well. Furthermore, our assumption allowed us to ignore the fact that most upward radiation is not vertical, but at some angle to the vertical. Radiation traveling at 60° to the vertical will pass through 6 km of air as it ascends through a 3-km layer, and so is more likely to be absorbed by the layer. But if we assume that the 3-km layer is either perfectly transparent or absolutely opaque, we conclude that radiation of a particular wavelength will either pass entirely through the layer or be entirely absorbed by the layer, regardless of its direction of travel.
Today we present our first layered-atmosphere computer model. The model does not assume that each layer is either transparent or opaque. When we calculate the power escaping into space from layer A at temperature T between wavelengths 10.0 μm and 10.1 μm, we proceed as follows. We start with the black-body radiation power density at wavelength 10 μm and temperature T. This power density is almost constant in the narrow range 10.0 μm to 10.1 μm, so we multiply the power density at 10.0 μm by 0.1 μm and obtain a good estimate of the power radiated between 10.0 μm and 10.1 μm. Now we multiply this power by the fractional absorption of layer A at 10.0 μm. The principle of radiative symmetry dictates that the efficiency with which a body emits radiation at a particular wavelength, as a fraction of the power emitted by a black body, is exactly equal to the efficiency with which it absorbs that same wavelength. So we now have the power radiated by layer A between wavelengths 10.0 μm and 10.1 μm. By assumption, whatever is not absorbed by the layer above A will escape into space, so we multiply the power radiated by A by the fractional transmission at 10.0 μm (that's one minus the fractional absorption at 10.0 μm) of the layer immediately above, and so arrive at the power between 10.0-10.1 μm that escapes from layer A into space.
To obtain the total power escaping into space from each layer, we add up the power escaping in all the 0.1-μm bands from 5 μm to 30 μm, which is the extent of our absorption spectra. We will include the surface of the Earth as its own layer. As we have in the past, we will assume the Earth's surface is a black-body radiator. Thus our program will calculate for us the total power escaping from the Earth into space, and allow us to see how much of this power is radiated by the surface and by each atmospheric layer.
Although we have dropped the transparent-opaque simplification, we retain two of its corollaries. First, we ignore the fact that most upward radiation is not vertical. Second, we assume that any radiation that manages to pass through the layer immediately above will be sure to pass through all remaining layers. These assumptions will effect our estimates, but we believe the effect will be less than 10%. In the future we may enhance our model to remove these assumptions, but for now we will start with a simple model.
We wrote our computer model in TclTk. You will find it here. The program takes as its input this file containing the names of the layers, their temperatures, and their absorption spectra. It produces the following output.
We see immediately that the power escaping from the 15-km layer is only 1.5% of the total escaping power, and twenty times less than the power escaping from the Earth's surface. The top three layers of the atmosphere combined contribute less than 10% to the total escaping power. These are the layers in which radiation is dominated by CO2. In the lower layers, radiation is dominated by water vapor.
Before we proceed with exercising our model, however, we must correct a deficiency in our existing spectra. Our spectra extend from 5 μm to 30 μm, but it turns out that a significant portion of the heat radiated by the Earth's atmospheric layers is radiated in the range 30 μm to 60 μm, as you can see in the graph below. (In case you are interested, we obtained the curves of this graph using this program.)
The "BB" column in our table gives the power a black body would radiate, as calculated using Stefan's Law. Our calculation assumes the Earth's surface is a black body, so when we see 401 W/m2 in the "BB" column, we expect to see the same value in the "Layer" column. But we don't, and the reason we don't is because our calculation adds up only the power radiated by each layer in the range 5 μm to 30 μm. A black body at 290 K radiates only 349 W/m2 in this range. The remaining 52 W/m2 it radiates in the range 30 μm to 60 μm.
We must go back to the Spectral Calculator and extend our spectra to 60 μm. While we are there, we will obtain the spectra for 660 ppm CO2 and 165 ppm CO2 as well.
In previous posts, we simplified our discussion by assuming that each atmospheric layer was either perfectly transparent or absolutely opaque at each wavelength. This assumption, combined with an examination of the absorption spectra, allowed us to say that all radiation passing through one layer would be sure to pass through all higher layers as well. Furthermore, our assumption allowed us to ignore the fact that most upward radiation is not vertical, but at some angle to the vertical. Radiation traveling at 60° to the vertical will pass through 6 km of air as it ascends through a 3-km layer, and so is more likely to be absorbed by the layer. But if we assume that the 3-km layer is either perfectly transparent or absolutely opaque, we conclude that radiation of a particular wavelength will either pass entirely through the layer or be entirely absorbed by the layer, regardless of its direction of travel.
Today we present our first layered-atmosphere computer model. The model does not assume that each layer is either transparent or opaque. When we calculate the power escaping into space from layer A at temperature T between wavelengths 10.0 μm and 10.1 μm, we proceed as follows. We start with the black-body radiation power density at wavelength 10 μm and temperature T. This power density is almost constant in the narrow range 10.0 μm to 10.1 μm, so we multiply the power density at 10.0 μm by 0.1 μm and obtain a good estimate of the power radiated between 10.0 μm and 10.1 μm. Now we multiply this power by the fractional absorption of layer A at 10.0 μm. The principle of radiative symmetry dictates that the efficiency with which a body emits radiation at a particular wavelength, as a fraction of the power emitted by a black body, is exactly equal to the efficiency with which it absorbs that same wavelength. So we now have the power radiated by layer A between wavelengths 10.0 μm and 10.1 μm. By assumption, whatever is not absorbed by the layer above A will escape into space, so we multiply the power radiated by A by the fractional transmission at 10.0 μm (that's one minus the fractional absorption at 10.0 μm) of the layer immediately above, and so arrive at the power between 10.0-10.1 μm that escapes from layer A into space.
To obtain the total power escaping into space from each layer, we add up the power escaping in all the 0.1-μm bands from 5 μm to 30 μm, which is the extent of our absorption spectra. We will include the surface of the Earth as its own layer. As we have in the past, we will assume the Earth's surface is a black-body radiator. Thus our program will calculate for us the total power escaping from the Earth into space, and allow us to see how much of this power is radiated by the surface and by each atmospheric layer.
Although we have dropped the transparent-opaque simplification, we retain two of its corollaries. First, we ignore the fact that most upward radiation is not vertical. Second, we assume that any radiation that manages to pass through the layer immediately above will be sure to pass through all remaining layers. These assumptions will effect our estimates, but we believe the effect will be less than 10%. In the future we may enhance our model to remove these assumptions, but for now we will start with a simple model.
We wrote our computer model in TclTk. You will find it here. The program takes as its input this file containing the names of the layers, their temperatures, and their absorption spectra. It produces the following output.
------------------------------------------------The "Layer" column is the power radiated upwards by each square meter between 5 μm and 30 μm. The "Escaping" column is the power that escapes. We used 290 K for the surface temperature, which is 17°C. The total power escaping into space is 268 W/m2. We don't have radiation from the 18-km layer, because we use this layer only as an absorber for radiation from the 15-km layer. The atmosphere above 15 km plays little or no part in atmospheric convection because it is above the tropopause.
Name Temp BB Layer Escaping
------------------------------------------------
Surface 290.0 401.1 349.0 89.7
0-km 280.0 348.5 225.3 58.8
3-km 270.0 301.3 150.0 49.8
6-km 250.0 221.5 81.5 44.4
9-km 230.0 158.7 31.2 15.4
12-km 220.0 132.8 16.3 5.8
15-km 220.0 132.8 13.1 4.2
------------------------------------------------
Total: 268.2
------------------------------------------------
We see immediately that the power escaping from the 15-km layer is only 1.5% of the total escaping power, and twenty times less than the power escaping from the Earth's surface. The top three layers of the atmosphere combined contribute less than 10% to the total escaping power. These are the layers in which radiation is dominated by CO2. In the lower layers, radiation is dominated by water vapor.
Before we proceed with exercising our model, however, we must correct a deficiency in our existing spectra. Our spectra extend from 5 μm to 30 μm, but it turns out that a significant portion of the heat radiated by the Earth's atmospheric layers is radiated in the range 30 μm to 60 μm, as you can see in the graph below. (In case you are interested, we obtained the curves of this graph using this program.)

The "BB" column in our table gives the power a black body would radiate, as calculated using Stefan's Law. Our calculation assumes the Earth's surface is a black body, so when we see 401 W/m2 in the "BB" column, we expect to see the same value in the "Layer" column. But we don't, and the reason we don't is because our calculation adds up only the power radiated by each layer in the range 5 μm to 30 μm. A black body at 290 K radiates only 349 W/m2 in this range. The remaining 52 W/m2 it radiates in the range 30 μm to 60 μm.
We must go back to the Spectral Calculator and extend our spectra to 60 μm. While we are there, we will obtain the spectra for 660 ppm CO2 and 165 ppm CO2 as well.
Wednesday, September 15, 2010
CO2 Absorption Band
In our previous post, we presented this graph of absorption by the Earth's atmosphere between 18 km and 21 km. This absorption is due entirely to CO2. In our calculations we set water vapor concentration to zero. Indeed, the absorption in the range 13-17 μm is due almost entirely to CO2 starting at an altitude of 9 km. The following plot gives us a close-up of the CO2 absorption in 3-km layers.
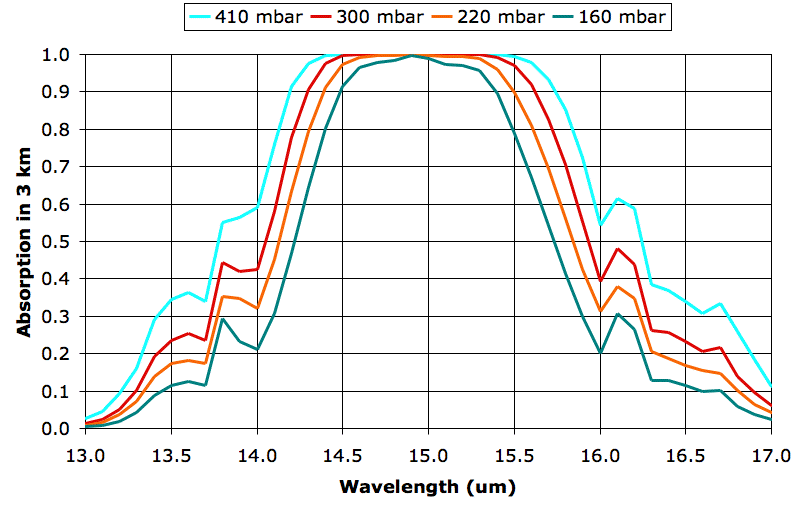
The four graphs are for 9, 12, 15, and 18 km, but we have named them after their atmospheric pressures, 410, 300, 220, and 160 mbar respectively. These pressures do not, in fact, correspond exactly to the pressures we observe in the atmosphere, because our pressure calculation ignores the drop in temperature as we ascend, but we used these pressure values when we calculated the spectra.
What we see between the absorption at 160 mbar and 300 mbar is the effect of doubling the density of CO2 molecules. In both cases, CO2 concentration is 330 ppm, which means 330 out of every 1,000,000 molecules are CO2. But the number of molecules per cubic meter increases approximately with the pressure, so the 300-mbar plot represents twice as much CO2 per cubic meter as the 160-mbar plot.
The absorption at 160 mbar for wavelength 14 μm is 21%, rising to 99% at 15 μm. The absorption at 300 mbar for wavelength 14 μm is 42%, rising to 99% at 15 μm. Twice as much CO2 in a 3-km layer leads to twice as much absorption of 14-μm radiation, but no significant increase in absorption of 15-μm radiation. We are particularly interested in the effect of doubling CO2 concentration, so let us try to get a better idea of how much more absorbing power the atmosphere has at 300 mbar than 160 mbar. Suppose a lower layer of the atmosphere emits uniformly in the band 13-17 μm, so that there is equal power in each 0.5-μm division of our graph. We can count squares under each graph and divide by the total number of squares to get the fraction of power absorbed by CO2 at each pressure. We come up with 43% at 160 mbar and 56% at 300 mbar.
Of course, the lower layers of the atmosphere do not radiate uniformly in the 13-17 μm band. Their radiation in this band is dominated by their own CO2, in accordance with radiative symmetry. The 300-mbar layer will receive radiation from the 410-mbar layer below it, and this radiation will have a power distribution that matches the 410-mbar layer's own absorption spectrum. At 14 μm, for example, the 410-mbar layer will radiate only 60% as much power as it does at 15 μm. In our spreadsheet we multiply the radiation spectrum of the 410-mbar layer by the absorption spectrum of the 300-mbar layer, and find that the 300-mbar layer absorbs 74% of the radiation arriving from the 410-mbar layer below. Meanwhile, the 160-mbar layer absorbs 70% of radiation from the 220-mbar layer below it.
The greenhouse effect causes a convection cycle in the Earth's atmosphere, which transports heat from the Earth's surface to the tropopause. All layers of the Earth's atmosphere up to the tropopause radiate heat out into space through the thinner, upper layers. As our previous posts have shown, radiation by the lower layers is dominated by water vapor, while radiation by the upper layers is dominated by CO2. Our calculations suggest that doubling the atmosphere's CO2 concentration will cause only a slight increase in the absorption and emission of radiation by the upper layers. In future posts, we will try to estimate how much this slight increase in absorption will raise the surface temperature of the Earth.

The four graphs are for 9, 12, 15, and 18 km, but we have named them after their atmospheric pressures, 410, 300, 220, and 160 mbar respectively. These pressures do not, in fact, correspond exactly to the pressures we observe in the atmosphere, because our pressure calculation ignores the drop in temperature as we ascend, but we used these pressure values when we calculated the spectra.
What we see between the absorption at 160 mbar and 300 mbar is the effect of doubling the density of CO2 molecules. In both cases, CO2 concentration is 330 ppm, which means 330 out of every 1,000,000 molecules are CO2. But the number of molecules per cubic meter increases approximately with the pressure, so the 300-mbar plot represents twice as much CO2 per cubic meter as the 160-mbar plot.
The absorption at 160 mbar for wavelength 14 μm is 21%, rising to 99% at 15 μm. The absorption at 300 mbar for wavelength 14 μm is 42%, rising to 99% at 15 μm. Twice as much CO2 in a 3-km layer leads to twice as much absorption of 14-μm radiation, but no significant increase in absorption of 15-μm radiation. We are particularly interested in the effect of doubling CO2 concentration, so let us try to get a better idea of how much more absorbing power the atmosphere has at 300 mbar than 160 mbar. Suppose a lower layer of the atmosphere emits uniformly in the band 13-17 μm, so that there is equal power in each 0.5-μm division of our graph. We can count squares under each graph and divide by the total number of squares to get the fraction of power absorbed by CO2 at each pressure. We come up with 43% at 160 mbar and 56% at 300 mbar.
Of course, the lower layers of the atmosphere do not radiate uniformly in the 13-17 μm band. Their radiation in this band is dominated by their own CO2, in accordance with radiative symmetry. The 300-mbar layer will receive radiation from the 410-mbar layer below it, and this radiation will have a power distribution that matches the 410-mbar layer's own absorption spectrum. At 14 μm, for example, the 410-mbar layer will radiate only 60% as much power as it does at 15 μm. In our spreadsheet we multiply the radiation spectrum of the 410-mbar layer by the absorption spectrum of the 300-mbar layer, and find that the 300-mbar layer absorbs 74% of the radiation arriving from the 410-mbar layer below. Meanwhile, the 160-mbar layer absorbs 70% of radiation from the 220-mbar layer below it.
The greenhouse effect causes a convection cycle in the Earth's atmosphere, which transports heat from the Earth's surface to the tropopause. All layers of the Earth's atmosphere up to the tropopause radiate heat out into space through the thinner, upper layers. As our previous posts have shown, radiation by the lower layers is dominated by water vapor, while radiation by the upper layers is dominated by CO2. Our calculations suggest that doubling the atmosphere's CO2 concentration will cause only a slight increase in the absorption and emission of radiation by the upper layers. In future posts, we will try to estimate how much this slight increase in absorption will raise the surface temperature of the Earth.
Wednesday, September 1, 2010
The Earth's Tropopause
In our previous post, we noted that the temperature of the atmosphere does not drop by more than a few degrees Centigrade between altitude 12 km and 18 km. We concluded that altitude 15 km corresponds roughly to the atmosphere's tropopause, and therefore marks the top of its convection cycle. Today we consider if there is any significant heat transfer between the tropopause and the upper atmosphere.
The following graph shows the absorption of long-wave radiation by the seventh 3-km layer of the Earth's atmosphere, from altitude 18 km to 21 km. This line is the same as the 18-km line in our Earth's Atmosphere post. The absorption is typical of a clear day in April, at latitude 30°N. We assume water vapor content is zero, but CO2 concentration remains 330 ppm. We assume air pressure is 160 mbar and temperature is 210 K, or −63°C.
In the seventh layer, absorption by CO2 remains strong. As before, we say our 3-km layer is opaque at a particular wavelength when it absorbs more than 63% of that wavelength, and is transparent otherwise. The seventh 3-km layer is opaque from 14.3 to 15.6 μm, while the sixth layer was opaque to 14.3 to 15.7 μm. The seventh layer will absorb roughly 93% of the heat radiated upwards by the CO2 in the sixth layer.
We note that the actual pressure in the Earth's atmosphere at 18 km is closer to 130 mbar. We calculated atmospheric pressure using our constant-temperature model of atmospheric pressure, and this model starts to be increasingly inaccurate in the cold upper layers of the atmosphere.
When we chose our temperatures, we were looking at this plot and rounding to the nearest 10 K. If you look at the plot yourself, you will see that the minimum temperature varies with latitude, and that the minimum spreads over a large range. We see this variation with latitude and the extent of the minimum in plots like this one also. In the case of 30°N, the temperature minimum extends from roughly 12 km to 22 km. The tropopause is the altitude at which the temperature stops dropping with pressure as it would in adiabatic expansion. Thus the tropopause is not at the altitude of minimum temperature, but rather at the altitude where temperature stops dropping adiabatically with pressure.
We go back to this plot and estimate the tropopause altitude as 9 km at 90°N (the north pole), 12 km at 30°N, and 13 km at 0°N (the equator). Why is the tropopause higher in the tropics? Our model of the greenhouse effect and the atmospheric layers must provide us with an answer to this question.
We look at the water vapor concentration in this plot, we see that we have 10 ppm water vapor concentration up to roughly 9 km at 0°N, 12 km at 30°N, and 13 km at 0°N. As we saw in the fifth layer, water vapor concentration of 10 ppm marks the altitude at which the atmosphere becomes transparent to wavelengths 5 to 9 μm, thus allowing the atmosphere below to radiate these wavelengths into space. Between 12 km and 21 km there is no significant change in the absorption spectrum of the atmosphere. A large body of air rising from 12 km to 21 km will be unable to radiate heat into space as it rises. If it cannot radiate heat, it will not sink, and so we will have no convection. Thus we expect the convection cycle to stop at the altitude where water vapor concentration drops to around 10 ppm, and this is indeed what we observe in the Earth's atmosphere.
There is no significant drop in temperature for at least 10 km above the tropopause. Without a temperature gradient, there can be no heat transport by conduction. There is no significant change in the absorption spectrum as we ascend these 10 km, so each layer of the atmosphere will receive as much heat by radiation from the layers above and below as it radiates back to those same layers. Thus there can be no significant heat transport by radiation either. We have already concluded that convection stops at the tropopause, so we see that there is no significant heat exchange between the tropopause and the atmosphere above it.
The following graph shows the absorption of long-wave radiation by the seventh 3-km layer of the Earth's atmosphere, from altitude 18 km to 21 km. This line is the same as the 18-km line in our Earth's Atmosphere post. The absorption is typical of a clear day in April, at latitude 30°N. We assume water vapor content is zero, but CO2 concentration remains 330 ppm. We assume air pressure is 160 mbar and temperature is 210 K, or −63°C.

In the seventh layer, absorption by CO2 remains strong. As before, we say our 3-km layer is opaque at a particular wavelength when it absorbs more than 63% of that wavelength, and is transparent otherwise. The seventh 3-km layer is opaque from 14.3 to 15.6 μm, while the sixth layer was opaque to 14.3 to 15.7 μm. The seventh layer will absorb roughly 93% of the heat radiated upwards by the CO2 in the sixth layer.
We note that the actual pressure in the Earth's atmosphere at 18 km is closer to 130 mbar. We calculated atmospheric pressure using our constant-temperature model of atmospheric pressure, and this model starts to be increasingly inaccurate in the cold upper layers of the atmosphere.
When we chose our temperatures, we were looking at this plot and rounding to the nearest 10 K. If you look at the plot yourself, you will see that the minimum temperature varies with latitude, and that the minimum spreads over a large range. We see this variation with latitude and the extent of the minimum in plots like this one also. In the case of 30°N, the temperature minimum extends from roughly 12 km to 22 km. The tropopause is the altitude at which the temperature stops dropping with pressure as it would in adiabatic expansion. Thus the tropopause is not at the altitude of minimum temperature, but rather at the altitude where temperature stops dropping adiabatically with pressure.
We go back to this plot and estimate the tropopause altitude as 9 km at 90°N (the north pole), 12 km at 30°N, and 13 km at 0°N (the equator). Why is the tropopause higher in the tropics? Our model of the greenhouse effect and the atmospheric layers must provide us with an answer to this question.
We look at the water vapor concentration in this plot, we see that we have 10 ppm water vapor concentration up to roughly 9 km at 0°N, 12 km at 30°N, and 13 km at 0°N. As we saw in the fifth layer, water vapor concentration of 10 ppm marks the altitude at which the atmosphere becomes transparent to wavelengths 5 to 9 μm, thus allowing the atmosphere below to radiate these wavelengths into space. Between 12 km and 21 km there is no significant change in the absorption spectrum of the atmosphere. A large body of air rising from 12 km to 21 km will be unable to radiate heat into space as it rises. If it cannot radiate heat, it will not sink, and so we will have no convection. Thus we expect the convection cycle to stop at the altitude where water vapor concentration drops to around 10 ppm, and this is indeed what we observe in the Earth's atmosphere.
There is no significant drop in temperature for at least 10 km above the tropopause. Without a temperature gradient, there can be no heat transport by conduction. There is no significant change in the absorption spectrum as we ascend these 10 km, so each layer of the atmosphere will receive as much heat by radiation from the layers above and below as it radiates back to those same layers. Thus there can be no significant heat transport by radiation either. We have already concluded that convection stops at the tropopause, so we see that there is no significant heat exchange between the tropopause and the atmosphere above it.
Wednesday, August 25, 2010
The Sixth 3-km Layer
The following graph shows the absorption of long-wave radiation by the sixth 3-km layer of the Earth's atmosphere, from altitude 15 km to 18 km. This line is the same as the 15-km line in our Earth's Atmosphere post. The absorption is typical of a clear day in April, at latitude 30° North. Water vapor content is only 1 ppm, which is one tenth thousandth the concentration in the surface layer. But CO2 concentration is 330 ppm, which is the same as in the surface layer. Air pressure is 220 mbar, which is 22% of the pressure in the surface layer. What is striking about the sixth layer is that the temperature is 220 K, or −53°C, which is the same as in the fifth layer.
In the sixth layer, absorption by water vapor is nowhere more than 5%. But absorption by CO2 remains strong. As before, we say our 3-km layer is opaque at a particular wavelength when it absorbs more than 63% of that wavelength, and is transparent otherwise. The sixth 3-km layer is opaque from 14.3 to 15.7 μm and transparent otherwise. The fifth layer, immediately below, is opaque to 14.2 to 15.8 μm. It radiates in these wavelengths also. The sixth layer absorbs 90% of the heat radiated upwards by the fifth layer, but the remaining 10% will pass out into space.
The fifth and sixth layers are at the same temperature. We did not make up the temperatures, pressures, and concentrations we use in our 3-km atmospheric layers. We obtained them from actual measurements of the Earth's atmosphere.
We have talked at length about the tropopause that exists at the top of the convection cycle in an atmospheric greenhouse. In our simple examples, the tropopause marks the top of the convection cycle, and occurs when the atmosphere above becomes so thin as to allow heat to radiate directly into space. The Earth's atmosphere is not so simple as in our examples. Above 12 km, the Earth's atmosphere is transparent to most long-wave radiation, but remains opaque in the narrow band that is absorbed by CO2. At a high enough altitude, this CO2 will become thin enough that it becomes transparent. But the tropopause of the Earth's atmosphere appears to occur at a lower altitude. It occurs when the atmosphere is transparent to over 90% of long-wave radiation.
In later posts, we will see how absorption by ozone in the stratosphere effects our greenhouse convection cycle. In the meantime, we will accept that there is very little change in temperature from altitude 12 km to 18 km, and therefore these altitudes mark the top of the Earth's greenhouse convection cycle.

In the sixth layer, absorption by water vapor is nowhere more than 5%. But absorption by CO2 remains strong. As before, we say our 3-km layer is opaque at a particular wavelength when it absorbs more than 63% of that wavelength, and is transparent otherwise. The sixth 3-km layer is opaque from 14.3 to 15.7 μm and transparent otherwise. The fifth layer, immediately below, is opaque to 14.2 to 15.8 μm. It radiates in these wavelengths also. The sixth layer absorbs 90% of the heat radiated upwards by the fifth layer, but the remaining 10% will pass out into space.
The fifth and sixth layers are at the same temperature. We did not make up the temperatures, pressures, and concentrations we use in our 3-km atmospheric layers. We obtained them from actual measurements of the Earth's atmosphere.
We have talked at length about the tropopause that exists at the top of the convection cycle in an atmospheric greenhouse. In our simple examples, the tropopause marks the top of the convection cycle, and occurs when the atmosphere above becomes so thin as to allow heat to radiate directly into space. The Earth's atmosphere is not so simple as in our examples. Above 12 km, the Earth's atmosphere is transparent to most long-wave radiation, but remains opaque in the narrow band that is absorbed by CO2. At a high enough altitude, this CO2 will become thin enough that it becomes transparent. But the tropopause of the Earth's atmosphere appears to occur at a lower altitude. It occurs when the atmosphere is transparent to over 90% of long-wave radiation.
In later posts, we will see how absorption by ozone in the stratosphere effects our greenhouse convection cycle. In the meantime, we will accept that there is very little change in temperature from altitude 12 km to 18 km, and therefore these altitudes mark the top of the Earth's greenhouse convection cycle.
Subscribe to:
Posts (Atom)
