Earth Radiator

Following our discussion of black bodies and our calculation of solar heat, we now consider whether or not the Earth acts as a black-body radiator.

In an earlier graph we show how a body at 200 K (−70°C) radiates at infrared wavelengths 6 μm to 60 μm. In another graph we show how a body at 300 K (27°C) radiates at infrared wavelengths 4 μm to 40 μm. In Radiative Symmetry we showed that any particular object must emit and absorb any particular wavelength with equal efficiency. The extent to which the Earth is a black-body radiator at infrared wavelengths between 4 μm to 60 μm is the extent to which it is also a black-body absorber at these same wavelengths.

The Earth's atmosphere contains water droplets in the form of clouds, and also gaseous water in the form of water vapor, which we experience as humidity. As we showed in an earlier experiment, liquid water is black to infrared wavelengths. The following graph plots the absorption length of liquid water with wavelength. The data comes from three papers, Irvine et al, Sullivan et al, Hale et al, and Zolotarev et al, as provided here. We converted "absorption coefficient" in cm⁻¹ into "absorption length" or "penetration depth" in μm.





The absorption length or penetration depth, L, is the depth of water required to absorb 63% of incident radiation. We have A = 1 − e ^x/L, where A is the fraction absorbed and x is depth. (See here for another source of same plot, thanks to Teddy Cheung for link.) After depth 3L, absorption is 95%. As you can see from the graph, the largest value of L for wavelengths 4μm to 60μm is 80μm. Water 240 μm deep absorbs over 95% of all radiation between 4 μm and 60 μm.

Water droplets in clouds are roughly twenty microns in diameter, so each droplet absorbs a significant proportion of infrared radiation. We conclude that clouds are opaque to infrared. But what about water vapor? The following plot, provided by NASA, shows water vapor content by volume with altitude and latitude in the Earth's atmosphere. The color-coding is logarithmic. Light green corresponds to roughly 1 g/m³ (one gram per cubic meter). Black is missing data.





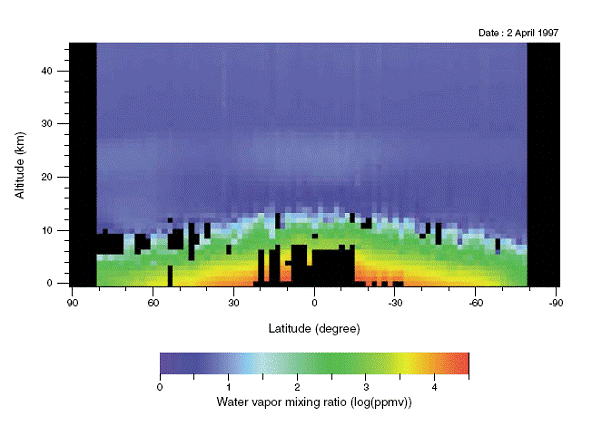
The atmosphere up to altitude 3 km contains at least 1 g/m³ water vapor for all latitudes. Liquid water has density 10⁶ g/m³. Radiation passing through air encounters one million times fewer water molecules per meter than air traveling through water. Suppose we assume a simple linear relationship between the concentration of water molecules and the absorption length. In that case, the absorption length of 1 g/m³ water vapor would be one million times longer than that of liquid water because the concentration of water molecules is one million times lower. Radiation must travel one million times farther in order to encounter as many water molecules as it would in pure water. Thus 240 μm of liquid water would have the same absorption as 240 m of air containing 1 g/m³ of water vapor. A 10-m thickness of the Earth's humid, lower atmosphere would absorb over 95% of infrared radiation between 4 μm and 60 μm.

But our astronomer friends tell us they can see through the atmosphere at infrared wavelengths. Our assumptions about water vapor cannot be correct. We will investigate the absorption spectrum of water vapor in future posts. The Earth's oceans, however, are made of liquid water, and they cover most of the globe. A thin layer of liquid water absorbs all infrared wavelengths. By the principle of radiative symmetry liquid water must be an efficient radiator of infrared wavelengths as well. Whether water vapor absorbs much infrared radiation or not, the Earth will be a good black-body radiator.