Circulating Cells

Today we present our new simulation program, Circulating Cells, Version 1, or CC1. The following picture shows the program's display shortly after we start it up. The array of cells represents a cross-section of the atmosphere. Each cell represents an equal mass of gas. The color of the cells indicates their absolute temperature, according to the legend at the top, with the exception of the black one. The black cell is black so we can watch it circulating around.

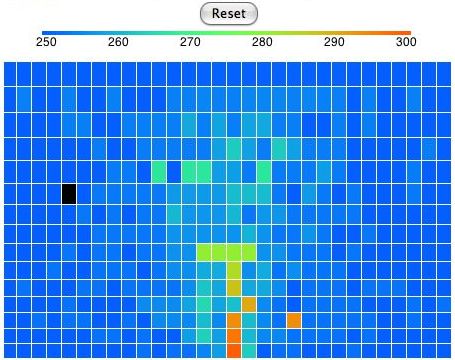
This version of the program heats one location on the bottom row. Any cell that enters this location we heat to 300 K. If the cell enters at a higher temperature, we let it keep its higher temperature. Thus we never remove heat from our array. The hot cells are rising, and as they rise they cool down. They turn from red to green. Meanwhile, cold cells must descend to make way for the hot cells. The cells that descend warm up. They turn from blue to green. At the beginning of our simulation, all the cells are blue. They are at 250 K. If we press Reset, all the cells will return to 250 K and the simulation will start again.

In our simulation, convection occurs by rotating blocks of four cells. The program picks a block of four cells at random. It calculates how much a quarter-turn will raise or lower the block's center of gravity. If a rotation will lower the center of gravity, the program performs the rotation. Otherwise, it does not. When the program rotates a block, one cell rises, one falls, and two stay at the same height. The one that falls contracts and warms up. The one that rises expands and cools down. The two cells that move sideways do not change temperature. But they may rise when they move from the top of a cold cell to the top of a hot cell. Hot cells are taller than cold cells. In the following picture we see the distribution of heat in the atmosphere after a few minutes of running. The black cell has moved. We can turn any cell into a black cell by clicking on it with the mouse. We can turn any black cell back into a normal cell by clicking it again.

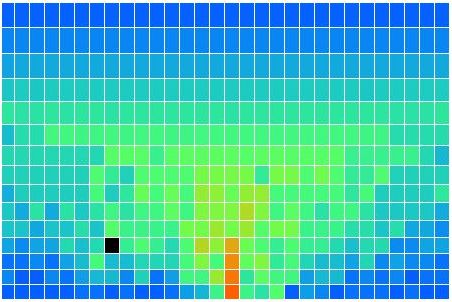
The simulation is made possible by a fundamental approximation. We arrange the cells as if the cells in each row are all at the same height, even though some may be sitting on top of columns of air that are significantly warmer or cooler than the others. Without this approximation, we cannot arrange the cells in an array, and simulation becomes several orders of magnitude more complex and time-consuming.

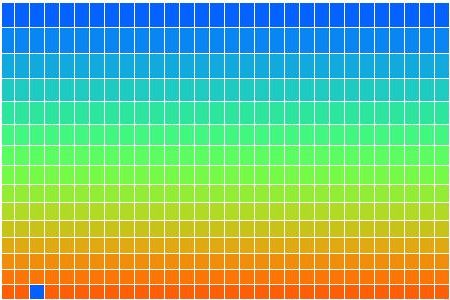
In CC1, there is no way for heat to pass from one cell to another. There is no conduction, no mixing, and no radiation. There is no way for heat to leave the array. After an hour of running, we end up with the following distribution of heat, all arising from the single heated location at the center of the bottom row. There is one blue cell on the bottom remaining. It moves around a bit, but so far it has resisted being drawn into the warm location.

Our program is written in TclTk. We encourage you to download the program and run it for yourself. Click here to download the program. Instructions for how to run the simulation on Linux, MacOS, and Windows are in the comments at the top of the program. Open CC_1.tcl with a text editor to read those instructions. Once the program is running, the movement of the cells is fascinating. Further comments in the program show how each routine works.

Without self-regulation by clouds we estimate that high clouds will warm the Earth by 38°C, doubling CO2 will warm the Earth by 1.5°C, and thick clouds will cool the Earth by 96°C. It is our hope that Circulating Cells will evolve into a simulation of radiation, convection, precipitation, and, ultimately, self-regulation by clouds. We will then be able to estimate the effect of doubling CO2 concentration within a self-regulating climate. That evolution may take another year or two, and maybe the task will prove too monumental for us. But I think it will be an enjoyable journey, no matter how it ends. So I hope you will accompany me.