Surface Cooling, Part II

In our Surface Cooling, Part I, we saw that the air above the ocean cools by less than 1°C at night. The air above the desert in Arizona, however, cools by 20°C at night. In Night and Day we saw that the heat radiated into space by the Earth is barely sufficient to cool the atmosphere by 1°C at night, let alone 20°C, so we are left wondering how the air above the desert can cool down so fast.

The table below presents the thermal properties of some common surface materials. We will make use of this table in future posts. Values for composite materials like wet soil are approximate. We picked values that are representative from resources like this, this, and this. Today we will use only the properties of dry sand. In the first column we have the thermal conductivity in Watt per meter per Kelvin (W/mK = W/m°C). A layer of material with thermal conductivity α, thickness d, temperature T_b at the bottom and T_t at the top, will conduct α(T_b−T_t)/d for each square meter of its surface area. A 10-cm thick layer of dry sand that is 20°C cooler on top than bottom will conduct 0.20 W/mK × 20 °C / 0.1 m = 40 W/m².

           Conductivity  Density   Capacity 
Material     (W/mK)     (kg/m^3)  (J/kgK)
Air           0.024        1.2       1000
Asphalt       0.75        1300        920
Copper         390        8900        420
Ice            2.2         910       2000
Mercury        8.7       14000        140
Sand, Dry     0.20        1600        830
Sand, Wet      4.0        2000       2500
Sandstone      1.7        2500        800
Soil, Dry      0.4        1300       1400
Soil, Wet      4.0        1500       2500
Snow, Light   0.10         100        420
Steel           43        7800        460
Water         0.58        1000       4200
Wood, Oak     0.17         770       1700

The second column gives the density in kilogram per cubic meter (kg/m³). A 10-cm layer of dry sand has mass 0.1 m × 1700 kg = 170 kg/m². The third column gives the specific heat capacity in Joule per kilogram per kelvin ( J/kgK = J/kg°C). A layer of material with specific heat capacity C, density ρ, and thickness d will require Cρd Joules of heat per square meter of surface area to raise its temperature by 1°C. A 10-cm thick layer of dry sand requires 800 J/kgK × 1700 kg × 0.1 m = 136 kJ/m² to warm up by 1°C. Alternatively, we must remove 136 kJ/m² to cool it by 1°C. If this layer loses loses 80 W/m², it will take half an hour to cool down by 1°C.

Our SC1 program simulates the cooling of the surface of the Earth at night. You can download it and run it yourself, by following the instructions in the code. The program works by dividing the surface material into thin layers and calculating the temperature of each layer in a sequence of small time steps. We assume the material is at a uniform temperature when it begins to cool, and that the heat loss from the upper surface is a constant 200 W/². In earlier versions of the code, we calculated the surface loss as a combination of radiation into space and convection with the surface air, but our results were pretty much the same, so we reverted to the assumption of constant loss to keep things simple.

The following graph shows what our simulation program tells us happens to dry sand at various depths in millimeters when it starts to cool from the surface at 200 W/m². We see the surface cools by 13°C in 1000s while the sand 40 mm down cools by roughly 0.1°C.



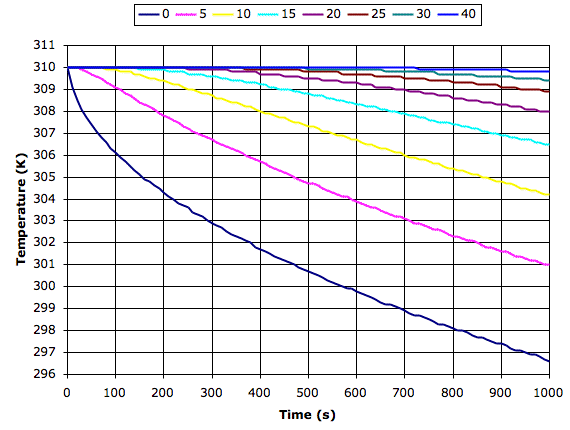
Materials with greater conductivity cool more slowly because heat rises from below to keep the surface warm. If we apply our simulation program to sandstone or asphalt, we find the surface cools down ten times more slowly than the surface of dry sand. So it is above dry sand or soil that we expect to see the greatest drop in surface temperature at night.

Our calculations show that a sandy surface can cool by 20°C at night. They show that one meter down, the heat of the day will hardly affect the temperature of the sand. But they still don't explain why the temperature above the desert sand cools by 20°C at night. The surface of the sand cools down because it loses heat to the air and to outer space. If anything, the cooling sand warms the air. We already know that the heat radiated by the air itself is not sufficient to cause such cooling. Indeed, our calculations show that it is impossible for air above the desert to cool by 20°C at night. And yet we know that a thermometer 2 m above the surface of the desert can register a drop of 20°C.

We conclude that the air above the sand at night cannot be the same air above the sand during the day, and indeed this conclusion leads us to a most satisfactory explanation for cold desert nights.