Simulated Planet Surface

Our Circulating Cells Version 8.3 simulates the planet surface with a row of blocks. You can download the latest code here. These blocks can be sand or water. If they are sand, they have low heat capacity and warm up quickly in the Sun's light. If they are water, they have high heat capacity and warm up slowly. By clicking upon one of the blocks, we change it from one type to the other.

In the long run, we will implement evaporation from the water blocks, but for now we concentrate upon the heat exchange between the surface and the atmosphere. In previous versions of our program, we allowed sunlight to pass directly into the surface gas cells. Now we allow sunlight to pass all the way through the entire atmosphere to be absorbed at a solid or liquid surface. Real water reflects 4% of short-wave radiation, and sand reflects something like 10%, but our simulated water and sand absorbs all short-wave radiation.

Both sand and water are near-perfect emitters of long-wave radiation, so we allow our surface blocks to radiate heat according to Stefan's Law. We also allow heat to leave the surface blocks by convection. We determine the convection heat loss by multiplying the temperature difference between the surface and the gas by a convection coefficient. This heat leaves the surface block and enters the gas cell above.

As we described in our previous post, our simulated atmosphere is partially-transparent, to an extent specified by the transparency fraction, τ. The gas above a surface block absorbs a fraction 1−τ of the block's radiation, and the remainder passes out into space. We add the absorbed heat to the gas cell above the surface block.

Now we come to a component in the heat exchange between the atmosphere and the surface that we have not simulated or calculated before. The atmosphere itself will radiate heat downwards towards the surface, and the surface, being a perfect absorber of such radiation, will absorb all of it. The heat radiated downward by the atmosphere is often called back-radiation or downward long-wave radiation. To calculate the back-radiation, we use the same equation we applied to the tropopause in our previous post. When the transparency fraction is 0.5, the gas radiates half as much heat as a black body at the same temperature.

We ran our simulation with Day heating of 350 W/m², all surface blocks made of sand, convection coefficient 20 W/m²K, and transparency fraction 0.50. The following figure shows the equilibrium state of the array. The surface blocks are color-coded for temperature in the same way as the gas cells, but they have an orange border to mark them as sand. A water cell has a blue border. You will find the equilibrium state of the array saved as a text file here.



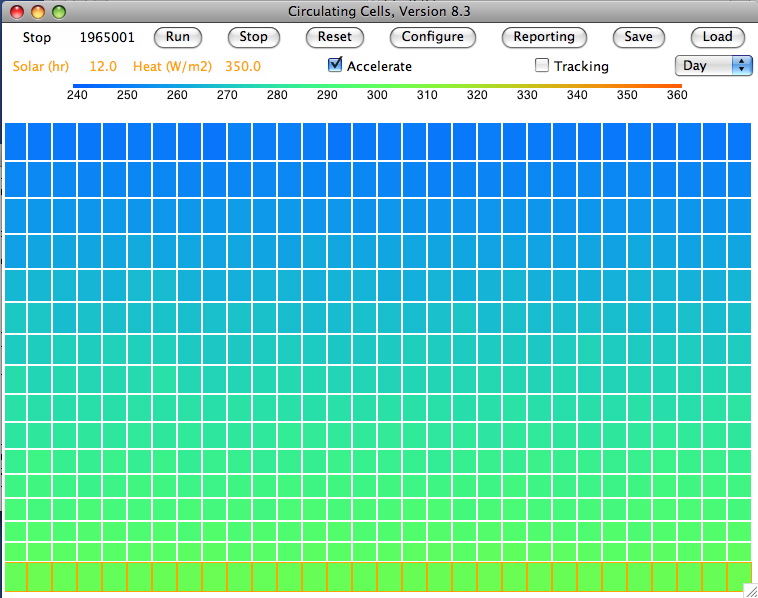
As in our previous simulations, the temperature drop from the surface gas cells to the tropopause gas cells is very close to 50 K. The sandy surface settles to 303.0 K, at which temperature it radiates 480 W/m². Of this, 240 W/m² passes directly into space and 240 W/m² is absorbed by the gas above. The tropopause settles to 249.0 K and radiates 110 W/m² into space. The total radiation into space is 350 W/m², which is the amount that is arriving from the sun, so our planet is in thermal equilibrium.

The 110 W/m² radiated by the tropopause must pass up through the atmosphere by convection. The surface gas is at an average temperature of 298.5 K, radiating 226 W/m² back to the surface. Thus a net 14 W/m² passes from the surface to the atmosphere by radiation. The remaining 96 W/m² passes into the atmosphere by convection at the surface. The surface is on average 4.5 K warmer than the gas, for which we expect only 90 W/m² to flow by convection. But the gas cells warm by roughly 8 K while they sit upon the sand. When they first arrive from above, they are almost 10 K cooler, and 200 W/m² flows into them by convection. Just before they rise up, they are only 2 K cooler, at which point only 40 W/m² flows into them. When we get the program to print out the convection rate, we obtain an average of 96 W/m², so all the heat from the Sun is accounted for.

We note that almost all the heat flowing from the surface to the atmosphere is carried by convection. The heat radiated by the surface and absorbed by the atmosphere is nearly balanced by the radiation returned by this same atmosphere. The difference is only 14 W/m², compared to 96 W/m² passing into the gas by convection. In our next post, we will simulate night and day over a sandy desert and see if we come up with reasonable variations in temperature at the sandy surface, the air above the surface, and the air high up in the tropopause.

Simulated CO2 Doubling

In Planetary Greenhouse we considered an atmosphere transparent to some long-wave radiation and opaque to others. In Circulating Cells Version 8.2, which you can download here, we simulate such an atmosphere with the new transparency fraction parameter.

For the moment, we ignore the temperature difference that must exist between the planet surface and the lower atmosphere (see Surface Cooling, Part VI). We assume that the solid or liquid surface beneath one of the bottom gas cells will be at the same temperature as the gas itself. Ever since our Earth Radiator post, we have assumed that the surface of a planet is a black body radiator. If a bottom cell is at 300 K, the surface below will be at 300 K also, and by Stefan's Law it will radiate 460 W/m². At 303 K, the radiated power increases to 480 W/m². Black-body radiation increases as the fourth power of the temperature, so a 1% increase in temperature causes a 4% increase in radiated power.

The absorption spectrum of the Earth's atmospheric layers varies in a complex and dramatic way with wavelength, as you can see here. What made our Total Escaping Power calculation so complicated was that we had to deal with the partial absorption of some wavelengths by each atmospheric layer, and therefore the partial emission of these same wavelengths by the same atmospheric layers. We want to avoid the complexity of partial absorption at a given wavelength, so we assume that the gas in our CC8 simulation has a spectrum that vacillates between perfect transparency to perfect opacity, and does so every fraction of a micron on the wavelength scale. As a result of this vacillation, a gas cell will absorb none of the radiation at a particular wavelength, or all of it. When we look at the fraction of black-body radiation that passes through a cell, this fraction is a constant property of the cell, regardless of its temperature or pressure. We call it the transparency fraction in the CC8 program, and here we will call it τ.

By the principle of radiative symmetry, each gas cells will radiate heat at the same wavelengths it absorbs. But because all the cells around it have the same absorption spectrum, none of the heat radiated by a cell will escape into space, except for the heat radiated by the cells in the top row, which we call our tropopause. These cells radiate directly into space. The power they radiate is the power that a black body would radiate, multiplied by 1−τ.

The incoming heat from the Sun, meanwhile, passes straight through our atmosphere, because we assume that the gas is perfectly transparent to short-wave radiation. The Sun's heat warms the planet surface, which for the moment we assume is something like sand. The sand heats up rapidly until it is losing heat by radiation and convection at the same rate it is gaining heat by absorption of the Sun's light. Some heat it radiates directly into space. The rest passes into the lower atmosphere and must be transported up to the tropopause by convection, where it is radiated into space.

Bottom Gas Cell Temperature = T_B
Planet Surface Temperature = T_S = T_B
Stefan's Constant = σ = 5.7 × 10⁻⁸ W/m²/K⁴
Emitted Surface Radiation = σ(T_S)⁴
Escaping Surface Radiation = τσ(T_S)⁴
Top Gas Cell Temperature = T_T
Emitted Tropopause Radiation = σ(1-τ)(T_T)⁴

We set τ=0.50 and ran CC8 with Day heating and the Sun's power set to 350 W/m². After ten million iterations we are confident that we have reached equilibrium, and we obtain this array. The average temperature of the bottom cells is 301.1 K (28°C) and of the top cells is 252.1 K (−21°C). The heat radiated by the surface is 468.5 W/m², of which 234.2 W/m² escapes directly into space. That leaves 115.7 W/m² of the Sun's heat to be transported up through the atmosphere. The heat radiated by the tropopause is 115.1 W/m², leaving 0.7 W/m² unaccounted for, which is well within the range of our rounding errors and the random fluctuations in our cell temperatures.

In our previous post, we ran our simulation for an opaque atmosphere, which corresponds to τ=0.00, and the surface temperature rose to 355 K (59°C). We see that τ=0.50 allows the surface to cool by 31°C to 28°C. In With 660 ppm CO2, we showed that doubling the CO2 concentration in the Earth's atmosphere will cause a 2% drop in the total escaping power. So now we set τ=0.49, so as to cause a 2% drop in the power escaping directly from our simulated planet surface into space. We arrive at a this array, in which the surface has warmed by 0.9°C to 302.0 K and the tropopause has warmed by 0.4°C to 252.5 K.

As a check, we run with τ=1.00, in which case the atmosphere is perfectly transparent and the surface radiates all its heat directly into space. The surface cools to 280 K (7°C). The atmosphere assumes the dry adiabatic lapse profile. But now we turn on the cell mixing by setting the mixing fraction to 0.2, and after a few hundred thousand iterations we see the entire atmosphere warm up to 280 K. This is the warm atmosphere we described in our original Greenhouse Effect post and again in Adiabatic Magic. When the atmosphere is not transporting heat to the tropopause, there is no greenhouse effect, and the atmosphere mixes until it arrives at a uniform temperature equal to the surface temperature.

We see that CC8 can simulate the effect of changing the concentration of a greenhouse gas like CO2, simply by making small changes to its transparency fraction. Once we have included evaporation, clouds, and rain into our simulation, we will be able to estimate the effect of changes in CO2 upon the average temperature of our planet surface.

Black-Body Tropopause

Our CC7 program provides six different ways to heat the atmospheric cell array. In CC8, we eliminate most of these and replace them with only three: Day, Night, and Cycle. The others were useful in checking the performance of the simulation, but are no longer necessary. Because we now have a good understanding of the relationship between simulation time, impetus for circulation, and program iterations, we are now able to express the Sun's heat in W/m² instead of the less realistic K/iteration of our earlier programs. We represent the incoming solar power with Q_sun instead of the previous Q_heating. Furthermore, we can use Stefan's Law directly upon the top cells, as if they were black and the gas above them were transparent. Our program now contains a value for Stefan's Constant, which we set to 5.7×10⁻⁸.

For our convenience, we display the time of day in hours in the main window. Time 12.0 hr is noon, when the Sun is certain to shine, and midnight is 0.0 hr. We display the current solar power in W/m². Previously, we applied a sinusoidal variation in the Sun's power during the day, but now we simply turn the Sun's power on to Q_sun during daylight hours, and to zero during the night. As before, however, the Sun will shine for a fraction of the day given by day_fraction.

We run the program with Day heating and the Sun's power set to 350 W/m². We have ke_fraction at 0.0 and we un-check left_only. Our cells have mass 333 kg/m². Their specific heat capacity at constant pressure is 1 kJ/K. Thus the lower cells warm up at 0.001 K/s, which matches our previous Q_heating of 0.001 K/iteration. We allow the array to reach equilibrium, which takes a long time: five million iterations, or one hours on our lap-top. You will find the equilibrium state in Day_1.txt. You can load it into CC8 with the Load button. At equilibrium, the top row's average temperature is 280.0 K. Applying Stefan's Law, the top cells should radiate 350 W/m², which is what we expect, since that's what we are putting in. The surface cell average temperature is 335.4 K, giving us the 55-K drop from the surface to the tropopause. This drop is consistent with our previous results.

We run the program with Q_sun set to 700 W/m² and Cycle heating to simulate day and night. We have day_fraction set to 0.5. After a million iterations we see the temperature of the bottom and top rows varying by a few degrees during night and day, as we did in Rotating Greenhouse.

The equilibrium surface temperature of 59°C (335 K) is much hotter than the surface of the Earth (around 14°C), even though 350 W/m² is the average power of the Sun. The Earth is cooler because its surface and lower atmospheric layers are able to radiate almost half their heat directly into space, assuming there is no cloud cover (see Total Escaping Power and subsequent posts).

Our next step is to allow the surface cells to radiate directly into space, and we will see how the surface cools down as a result. We must implement the surface and tropopause radiation before we can model the effect of clouds.