Impetus by Enthalpy

In Impetus Dissected we showed that impetus for circulation is the sum of buoyancy work and expansion work. In terms of the diagram below, the sum of the buoyancy work and expansion work is Mgδh. The work available per kilogram of gas in the four cells is simply gδh/4. Today we show that we can obtain this same answer with a calculation based upon enthalpy.



If we ignore kinetic energy, the specific enthalpy of a gas (that's the enthalpy per kilogram) is CpT + gz, where z is the altitude of the cell. When we heat up cell A by δT we increase its specific enthalpy by ΔH1.

ΔH1 = δTCp+gδh/2

This is the energy required to bring about the change in the temperature of cell A, and includes the work required to raise up the cells above A as well as the work required to increase the internal energy of A, and the work required to raise A's own weight.

For an ideal gas cell, we have pV=MRT, and from this we deduce that δh = mRδT/p, where m is the mass per square meter of the cell's bottom surface. Thus we have the following expression for ΔH1.

ΔH1 = δT(Cp+mgR/2p)

When cell A rises, it cools by adiabatic expansion. It is now warmer by δT ' than cell B, and taller by δh'. Suppose we now allow A to cool by δT ', so that it becomes identical to cell B. Its enthalpy decreases by ΔH2, and the four cells and the gas above are in an identical state to the one they were in before we warmed cell A.

ΔH2 = δT 'Cp+gδh'/2

In buoyancy work we showed that δT ' = δT(1−Rmg/pCp). We also showed that δh' ≈ mRδT(1 + mgCv/pCp)/p. Using these relations, and the fact that mg≪p, we obtain the following expression for ΔH2 after several lines of simplification.

ΔH2 = δT(Cp−mgR/2p)

The expressions for ΔH1 and ΔH2 are identical, except the sign of the gravitational term is opposite. When subtract ΔH2 from ΔH1, we obtain the enthalpy per kilogram of cell A that has gone missing during the rotation.

ΔH1−ΔH2 = mgRδT/p = gδh

Enthalpy cannot go missing. Our expression for enthalpy ignores the kinetic energy of the cells when it should not. The kinetic energy of the cells after the rotation is equal to the enthalpy that is missing in our calculation. When we divide it among the mass of the four cells, the missing enthalpy is gδh/4, which is our impetus for circulation.

We performed the same enthalpy calculation for incompressible cells and obtained the same answer. We have arrived at the same expression for impetus by two different means, for both incompressible and compressible cells. We are now confident that our calculation is correct.

Impetus Dissected

We return now to the unanswered questions we raised in Impetus for Circulation. We noted that the values our simulation program calculated for buoyancy work and expansion work differed by only a few percent. This equality made us suspect that we were in fact looking at the same source of energy in two different ways. If so, then it would be incorrect to add them together, because we would be counting the same energy twice. But how could they be the same source of energy, when we know that convection occurs in incompressible fluids like water? Surely there must be buoyancy work in water, even if there is no expansion work? Today we will answer these questions.

The following variation on our well-used buoyancy diagram shows four cells of incompressible fluid. The cells do not expand or compress as we change their pressure. As we showed earlier, water is almost, but not quite, and incompressible fluid.



When an incompressible cell rises, it does no expansion work, so it does not cool down. Unlike convection in a compressible gas, convection in an incompressible fluid requires no temperature gradient from bottom to top. If all the cells are at the same temperature, they can move around freely by exchanging places with one another. None of them are going to cool down or heat up as their pressure changes.

Thus we begin with all four incompressible cells at temperature T and warm up cell A by δT. Cell A gets taller by δh and becomes buoyant. Cell A rises and the block of four cells rotates clockwise. Cell B slides off cell A and onto cell C. In doing so, it drops by δh and does work Mgδh.

Meanwhile, the fluid above the four cells does not move at all. The left cells are taller by δh before and after the rotation. Thus the incompressible cells do not have to do any work raising the fluid above them. The total buoyancy work remains Mgδh. The expansion work is zero, so the total work done by the rotation is Mgδh.

Let us return to the gas-filled cells depicted here. The buoyancy work consists of two components. The first component is the work done by cell B as it slides off cell A. This work is Mgδh, just as it is for an incompressible fluid. The second component is the work required lift the gas above the block.

When cell A rises, the combined height of the two left-hand cells increases by a small fraction of δh (the fraction is mgCvδh/pCp). The increase is small, but the weight of the gas that must be lifted is great (the weight is p). The work required to raise the upper gas is significant (the work is MgδhCv/Cp). After subtracting this work from the work done by cell B, we are left with a net buoyancy work of only MgδhR/Cp (for air, R/Cp is 0.29).

Unlike an incompressible cell, however, a gas cell does work as it expands. In Expansion Work we found that the warm, rising cell does MgδhCv/Cp more work as it expands than is required to compress the cold, falling cell. This expansion work turns out to be exactly equal to the work required to raise up the gas above the rotating block. When we add the buoyancy and expansion work together, we find that the total work done by the rotating cells is Mgδh, which is the same as the work done by the incompressible cells.

We see that buoyancy work and expansion work are separate sources of energy after all. In an incompressible fluid, we have only buoyancy work. The expansion work is zero. In a gas, we have both, but their sum is the same. This sum is what we call the impetus for circulation. Given a certain δh, the impetus for circulation is the same for both gas cells and incompressible cells. When the warm cell is taller by δh, the impetus for circulation is Mgδh.

In CC5, our calculation of buoyancy work ignored the work required to raise the upper gas, and so produced a value for buoyancy work that was incorrect, but equal to the impetus for circulation. Our calculation of expansion work, meanwhile, used Cp to multiply δT instead of Cv, and so produced a value for expansion work that was incorrect, but equal to the impetus for circulation. By accident, therefore, CC5 calculated the correct impetus for circulation in two different ways, and this was the origin of our mystery.

In our next post we will confirm today's argument by considering the enthalpy of incompressible and gas-filled cells. After that, we will return to enhancing our simulation, being confident that we understand the forces involved in the circulation of our atmospheric cells.

Expansion Work

Whenever we allow a block of four cells to rotate within our atmospheric simulation, we see a warm cell rise and expand while a cold cell falls and contracts. The expanding cell is larger, so it does more work than is required to compress the smaller, falling cell. In Impetus for Convection, we called the excess work done by the rising gas expansion work. Our CC5 program assumes the expansion work is equal to CpΔT, where Cp is the specific heat capacity of the gas at constant pressure, and ΔT is the drop in the average temperature of the rotating cells. Today we show that the correct value for expansion work is roughly one third less, and we find that its correct value is exactly equal to the work required to raise up the gas above the rotating block.

When a gas expands adiabatically, it does work pushing outwards, but no heat passes through its boundaries. By the First Law of Thermodynamics, the work done must be equal to the decrease in the internal heat of the gas. The internal heat of a kilogram of ideal gas is CvT, where Cv is its specific heat capacity at constant volume. A kilogram of gas that has cooled by ΔT through adiabatic expansion must have done CvΔT of work as it expanded. For air, Cv = 716 J/kgK, so this work would be 716 J/kg for a cooling of 1°C. If we multiply ΔT by Cp instead of Cv, we get a value 1003 J/kg, which is 313 J/kg too high.

Let us return to the four cells we considered in Buoyancy Work, and calculate the expansion work in terms of the same parameters. As before, we start with a block of four cells that has no tendency to circulate, and we warm the lower-left cell by δT. We use R for the specific gas constant. As always, we have Cp=R+Cv.



Before rotation, cell A is at T+δT. When it rises, it expands adiabatically from pressure p to p−mg. When mg≪p, the temperature drops by a factor of 1−Rmg/pCp. When cell B falls, it temperature begins at T(1−Rmg/pCp) and ends at T. A few lines of calculations will reveal that the drop in the average temperature of the four cells is simply δTRmg/4pCp. The expansion work, We, per kilogram of gas is:

We = δTRmgCv/4pCp

We have seen this quantity before. In Buoyancy Work we found that the work required to raise the gas above the block was δTRmgCv/4pCp. In our next post, we will explore the implications of this equality, and at last solve the mystery we presented in Impetus for Circulation.

Buoyancy Work

When a block of four cells in our atmospheric simulation rotates by convection, the center of mass of the block drops. In Impetus for Convection, we called the work done by the descending block buoyancy work. When we calculated buoyancy work with our CC5 program, we considered only the movements of the four cells within the rotating block. Today we present a calculation of buoyancy work that takes account of the work required to move the cells above the block, and we find that our original calculation over-estimated buoyancy work by more than a factor of three.

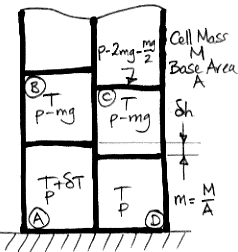
We start with a block of four cells that has no tendency to circulate, warm up the lower-left cell, and consider the buoyancy work this single warm cell can generate for us. Here is the diagram we presented in our Buoyancy post. The cell on the lower left is warmer by δT than the adiabatic profile we derived earlier. We use R for the specific gas constant, Cv for the specific heat capacity at constant volume, and Cp for the specific heat capacity at constant pressure. As always, we have Cp=R+Cv for an ideal gas.



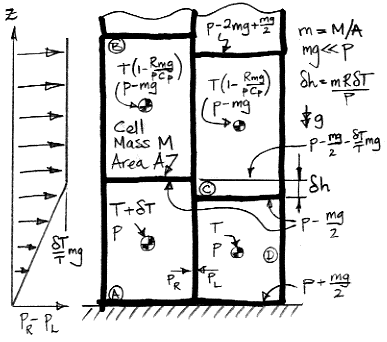
When a cell expands adiabatically from p to p−mg, its temperature drops from T to T(1−mg/p)^R/Cp. When mg≪p, this expression simplifies to T(1−Rmg/pCp), which is why the upper cells in our diagram have temperature T(1−Rmg/pCp).

As we heat cell A by δT, we raise its center of mass by δh/2 and the center of mass of cell B by δh. We also raise the gas above B by δh. Cells C and D do not move, nor does the gas above them. The weight of each cell is m per unit base area, and the weight of the gas above cell B is the pressure in cell B, which is p−mg. As we supply heat to A to warm it up, the work done by the expanding cell against gravity is W1.

W1 = mgδh + mgδh/2 + (p−mg)δh = mRδT(1 + mg/2p)

We now allow the four cells to rotate one step clockwise. Cells C and D move to the bottom. They are at temperature T. Cell B will be on the upper-right, with its temperature unchanged at T(1−Rmg/pCp). Cell A, having expanded adiabatically from pressure p to p−mg, will cool down, but will still be warmer than cell B by δT ' = δT(1−Rmg/pCp).

Suppose we remove heat from cell A until it is the same temperature as B. Once it has cooled by δT ', the block of four cells will be identical to the one we started with before we heated A by δT. As A cools by δT ', its center of mass drops by δh'.

δh' = mRδT '/(p−mg) = mRδT(1−Rmg/pCp)/(p−mg)

We note that mg≪p and this allows us to simplify the above expression.

δh' ≈ mRδT(1 + mgCv/pCp)/p

As cell A shrinks, its own center of mass drops by δh'/2 and the gas above drops by δh'. Now we can calculate the work done by gravity, W2, as the cell cools.

W2 = mgδh'/2 + (p−mg)δh' = δh'(p−mg/2) = mRδT(1 + mgCv/pCp)(1−mg/2p)

Once again we note that mg≪p, which allows us to simplify our expression.

W2 ≈ mRδT(1 + mgCv/pCp − mg/2p)

When we heated cell A by δT, we increased the gravitational potential energy of the cells and upper gas by and amount W1. When we allowed the cells to rotate, they produced buoyancy work, the size of which we would like to determine. When we allowed cell A to cool, we decreased the gravitational potential energy of the cells and upper gas by an amount W2, and in doing so we returned these gases to their original state. By conservation of energy, the difference between W1 and W2 must be equal to the buoyancy work.

W1−W2 = mRδT(Rmg/pCp)

The buoyancy work per kilogram of gas in the four cells, Wb, is therefore:

Wb = mgR²δT/4pCp

We interpret our expression for Wb as follows. When the cells rotate, cell B drops by δh, which does work mgδh = mgRδT/p. But at the same time, all the cells above A rise by δh'−δh>0, and this requires work mgRCvδT/pCp. The buoyancy work is the work done by B as it drops, minus the work required to raise the upper gas, divided by the mass of the four cells combined, which gives us the expression for Wb above. In our CC5 calculation, we ignored the work required to raise the upper gas, and so over-estimated the buoyancy work by a factor of Cp/R, which is 3.5 for air.

If cell B contains 300 kg/m² of air at 100 kPa and 300 K, and δT for cell A is 10°C, the buoyancy work is 6.2 J/kg, which is sufficient to accelerate the cells to 3.5 m/s. These cells would be 250 m high, so at 3.5 m/s they would circulate in one minute. Using our old calculation of buoyancy work, the circulation would take almost twice as long.

Buoyancy

The following diagram shows four cells sitting on a flat surface, just as four cells in our atmospheric simulation might sit upon the ground. We mark the center of mass of each with a cross-shaded circle. The cells each have mass M and base area A. The mass per unit area is m = M/A. Pressure drops from p in the lower cells to p−mg in the upper cells, where mg≪p.



The temperature of cell D is T. Cells B, C, and D have the same enthalpy. If D were to expand adiabatically from p to p−mg, it would cool to the same temperature as B and C. When gas expands adiabatically, Tp^R/Cp remains constant, where Cp is the heat capacity of the gas at constant pressure and R is the gas constant. When pressure scales by (1−mg/p), temperature scales by (1−mg/p)^R/Cp. Because mg≪p, the temperature of the upper cells is very close to T(1−Rmg/pCp).

Cell A has been warmed by a small amount δT compared to cell D. Because it is warmer, it is taller than cell D by δh=mRδT/p. Cell B rises above cell C by a distance δh, and cell A itself rises by δh/2 compared to cell D

In our simulation program, we assume the temperature and pressure within each cell is uniform. Here we allow for variation in pressure from the top to bottom. The top is at p−mg/2 and the bottom is at p+mg/2, so that the total change from top to bottom is mg.

At the top of cell D, the pressure is p−mg/2, but the pressure within A at the same height is greater by mgδT/T. On the left side of our diagram is a graph of the excess pressure in cell A with altitude. Cell A pushes sideways into cell D with an average pressure mgδT/2T. Cell B pushes upon cell C with average pressure mgδT/T, which is twice as much. Cell B starts to push its way over the top of cell C, and in doing so places some of its own weight upon cell D. This additional weight causes the pressure at the base of D increases, and now cell D starts to push its way under cell A, forcing it upwards.

Thus cell A becomes buoyant, and the four cells will rotate clockwise to allow A to rise. Buoyancy manifests itself not only as an upward force upon the buoyant cell, but also as horizontal forces upon the cells above and beside the buoyant cell. The cells above slide out of the way, and the cells beside it push inwards. It is only after these horizontal movements have begun that the buoyant cell can rise.