Enthalpy

The enthalpy of a volume of fluid is the energy it takes to replace this volume with an identical volume taken from a hypothetical infinite reservoir. Consider the following diagram. It shows a gas cell of volume V, pressure p, and temperature T at a height z. We show a pipe leading from the ground up to the base of the cell. A pressure valve allows gas to leave through another pipe when the cell pressure is greater than p. The cell is small enough that the pressure and temperature within it are uniform. We make the same assumption in our circulating cells simulation.



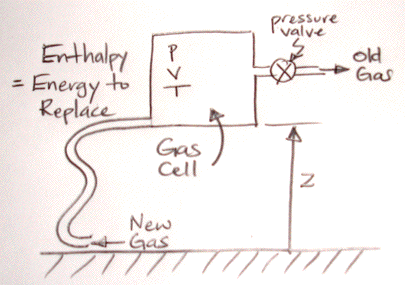
New gas entering at the lower-left corner of the cell must be at pressure p in order to force the old gas out of the pressure valve on the upper-right. Suppose the cross-section of the pipe is A and we push the gas in with a piston. The piston must move a total distance V/A to replace all the old gas. The front face of the piston must push with force pA. The work we do is pA×V/A = pV. The product pV is the pressure energy that we have mentioned before, but never explained in detail.

If we push the gas into the pipe at ground level, we have to do extra work to raise all the replacement gas up to the altitude of the cell. If the mass of the cell is m and gravity is g, the work we must do to raise the new gas is mgz. This is the gravitational energy component of enthalpy. When we use ρ for density, the gravitational energy becomes Vgzρ.

Our new gas must be at the same temperature as the old. We could choose 300 K as the temperature of the gas in our hypothetical reservoir. But we choose 0 K instead, because this eliminates a constant in our equations. The constant is of no use to us because we find that we are interested only in changes in enthalpy, never the absolute value of enthalpy.

Suppose our gas is ideal, with specific heat capacity at constant volume Cv. The heat required to warm up our replacement gas is mTCv. If we use Vρ for m the heat is TVρCv. The total energy required to replace the old gas in our cell with new gas from our hypothetical reservoir is the sum of the heat, gravitational energy, and pressure energy.

Enthalpy = H = pV + Vgzρ + TVρC_v

The specific enthalpy is the enthalpy per kilogram. We divide H by the mass Vρ to obtain the following, in which we use V to denote the volume per kilogram, which is the same as 1/ρ.

Specific Enthalpy = h = pV + gz + C_vT

For an ideal gas we have pV = RT, where R is the specific gas constant. We are already familiar with the heat capacity at constant pressure, Cp = R + Cv, so we arrive at the following expression for the specific enthalpy of an ideal gas.

h = (R + C_v)T + gz = C_pT + gz

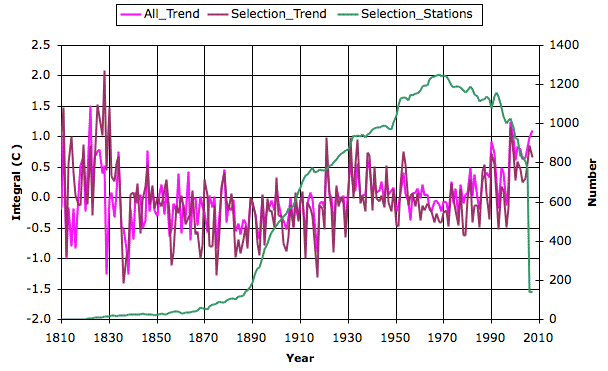
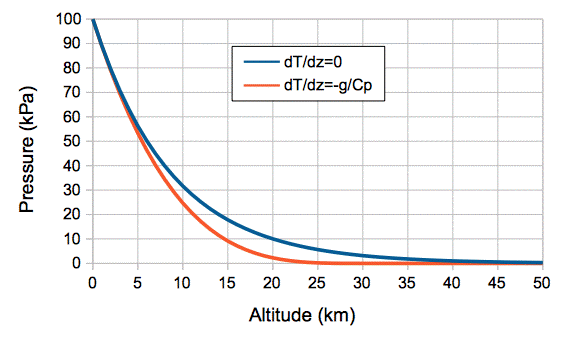
When we establish convection in an atmosphere, the variation in temperature with altitude must be such that no work is required to move volumes of gas up and down. We established this principle in a previous post and showed with a dozen lines of calculations that the variation of temperature with altitude must be linear with slope −g/Cp. Now let us make the same point using the concept of specific enthalpy.

The enthalpy of a kilogram of gas is the energy required to replace it from our hypothetical infinite reservoir. The energy required to move a kilogram of gas from one place to another in our atmosphere is the difference in its enthalpy at the two locations. Our assumption that no work is required to move gas up and down means that the specific enthalpy of the gas in the atmosphere must be constant with altitude.

dh/dz = C_pdT/dz + g = 0 ⇒ dT/dz = −g/C_p

And so we see that the concept of enthalpy allows us to deduce the dry adiabatic lapse rate in two lines instead of twelve. Enthalpy is a useful tool for calculations. But we note that the pressure and internal energy calculation we performed in our previous post is the one that shows us the physical mechanisms by which enthalpy is conserved, and is therefore important for our understanding.

We will use enthalpy in our next post to help solve the mystery of why expansion work and buoyancy work are equal in our circulating cells simulation.

The BEST Project

The Berkeley Earth Surface Temperature (BEST) has set out to re-calculate the global surface temperature trend. They describe the basis of their calculation here.

The first thing BEST addresses when they describe their calculation is the number of available weather stations, and how many of they should use to calculate a trend. We considered the same problem at length here and in brief here. According to BEST, there are around fifteen thousand weather stations reporting daily from 1970 to 2010. The Climatic Research Unit (CRU), the National Climatic Data Center (NCDC), and we ourselves based our calculations upon the GHCN station data. According to BEST, the GHCN data includes fewer than one in ten of the stations that recorded temperatures in 2000. The BEST team hope to use a greater fraction of the available stations.

BEST provided testimony to the US congress on 31st March. They have already applied their basic calculation to 2% of the fifteen thousand stations available in the period 1970 to 2010. They made no effort to correct for systematic errors like urban heating. And yet they arrive at a global surface temperature trend almost identical to that of CRU and NCDC. Here's what they have to say about this agreement.

The Berkeley Earth agreement with the prior analysis surprised us, since our preliminary results don’t yet address many of the known biases. When they do, it is possible that the corrections could bring our current agreement into disagreement. Why such close agreement between our uncorrected data and their adjusted data? One possibility is that the systematic corrections applied by the other groups are small. We don’t yet know.

We were just as surprised when we reproduced the CRU trend from the GHCN data by integrated derivatives. We used no reference grid. We used no corrections for systematic errors.

NASA estimates the urban heating effect in US weather stations to be roughly half a degree centigrade during the twentieth century (see our post here and NASA's paper here). But CRU claims that urban heating is either negligible or has been accounted for in their efforts. And NASA applies 0.5°C corrections and goes on to say that the corrected trend still shows a rise of 0.5°C in the twentieth century, and they claim this trend is accurate to ±0.1°C. We find all this confusing, and so do the people at BEST, which is why they are re-calculating the trend.

The GHCN inclusion criteria are another potential source of systematic bias in the trend. If we select stations from within the GHCN data set according to various criteria that appear to have nothing to do with temperature, we find that the trend alters in a significant way. The graph below shows the trend we obtain if we select from the GHCN data set only those stations that are reporting for at least 80% of the years between 1960-2000. We get a trend in which the 1930's are as warm as the 1990's.



We await with interest the BEST project's investigation of the effect of urban heating and station inclusion. We look forward to examining their trend-calculation algorithm. We have argued before that all such methods, with or without a reference grid, are pretty much equivalent, so we expect them to come up with something similar to the CRU and NCDC trends before they start to correct for systematic errors.

How BEST will correct for systematic errors in any meaningful or accurate way, we cannot say. If it was up to us, we would select long-lived stations in rural locations, and use the trends from those, even if there were only a dozen of them. But we have tried that already, and we get plots like the one above. The 1930s were hot, and it's just as hot now. But not especially hot.

Temperature, Pressure, and Altitude

In Impetus for Circultation, we were surprised to find that "expansion work" and "buoyancy work" were equal. In any circulation of gas cells, the excess work done by the pressure of hot, expanding gases is equal to the excess work done by the weight of cold, falling gases. We found this equality mystifying. Today we demonstrate a linear relationship between altitude and temperature that may or may not help solve the mystery.

As we saw in Adiabatic Balloons, it takes work to raise gas up from the lower atmosphere. If the temperature of the atmosphere is uniform, the rising gas gets cold as it expands, and is therefore more dense than its surroundings. It tends to sink. At the same time, it takes work to pull gas down from the upper atmosphere. The falling gas gets hot, and is therefore less dense than its surroundings, so it tends to rise.

In Planetary Greenhouse Simulation, we saw what happens when we heat the atmosphere from the bottom, and cool it from the top. The lower atmosphere heats up until a particular temperature profile develops: a linear drop of 50 K from the bottom to the top. Once this profile is established, convection occurs freely. As gas rises, it expands and cools, but the gas around it is already just as cool, so the rising gas continues rising. As gas falls, it compresses and warms, but the gas around it is already just as warm, so the falling gas continues falling. The temperature profile that allows convection is the profile generated by the expansion and compression of circulating gases.

We determined that we could ignore mixing between cells in our simulation. When a volume of gas expands without mixing, it does so according to the equation for adiabatic expansion. In Atmospheric Pressure we calculated pressure as a function of altitude for an atmosphere at constant temperature. Today we calculate pressure as a function of altitude for an atmosphere whose temperature varies with pressure as it would for a dry, ideal, gas expanding adiabatically.



We see that the temperature of an atmosphere stirred by convection must drop linearly with altitude. Michele has proved this to us a number of times, in different ways. The differential form of the result is:

dT/dz = − g/Cp
For dry air on Earth, we have g = 10 N/kg and Cp = 1 kJ/kgK, so we expect a drop of 10 K/km. Our simulation uses cells of dry air, and it shows a drop of around 50 K from bottom to top during convection. The temperature drops to 0 K at an altitude z_T = CpT₀/g. For T₀ = 300 K we have z_T = 30 km. When the temperature drops to O K, the pressure must be zero also. With a little more pencil-work, we arrive at the following equation for pressure with altitude.

p = p₀ (1 − gz/CpT₀)^Cp/R    (for dT/dx = −g/Cp)
The pressure at the bottom of our cell array is 100 kPa, and at the top is 50 kPa, with the bottom temperature at 300 K. The height of our array is 5.4 km, giving the simulation an average temperature drop of close to 10 K/km. In Atmospheric Pressure, we considered an atmosphere at uniform temperature, and arrived at the relation:

p = p₀e^−gz/RT    (for dT/dx = 0)
The atmosphere with uniform temperature never comes to a definite end, but keeps getting thinner and thinner with altitude.


Figure: Pressure versus Altitude for Constant Temperature (dT/dz=0) and Adiabatic Convection (dT/dz=−g/Cp) with T₀ = 300 K and p₀ = 100 kPa. The mass of the atmosphere is p₀/g = 10,000 kg/m² in both cases.
When our cell array is at a uniform temperature T = 250 K, the height of the array will be 5.0 km. Warming the atmosphere to initiate convection causes the top to rise by 400 m.

The −gz/Cp slope of the temperature profile is called the dry adiabatic lapse rate. The Earth's atmosphere is not dry. As moist air expands and cools, water condenses, which releases heat. Thus the wet adiabatic lapse rate is less than the dry adiabatic lapse rate. The lapse rate in the Earth's atmosphere appears to be 6 K/km.

Convection takes place when the temperature drops linearly with altitude. In an atmosphere stirred by convection, gravitational potential and atmospheric temperature are intimately related. A change in one will be matched by an equal and opposite change in the other.