The following variation on our well-used buoyancy diagram shows four cells of incompressible fluid. The cells do not expand or compress as we change their pressure. As we showed earlier, water is almost, but not quite, and incompressible fluid.
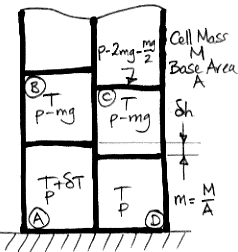
When an incompressible cell rises, it does no expansion work, so it does not cool down. Unlike convection in a compressible gas, convection in an incompressible fluid requires no temperature gradient from bottom to top. If all the cells are at the same temperature, they can move around freely by exchanging places with one another. None of them are going to cool down or heat up as their pressure changes.
Thus we begin with all four incompressible cells at temperature T and warm up cell A by δT. Cell A gets taller by δh and becomes buoyant. Cell A rises and the block of four cells rotates clockwise. Cell B slides off cell A and onto cell C. In doing so, it drops by δh and does work Mgδh.
Meanwhile, the fluid above the four cells does not move at all. The left cells are taller by δh before and after the rotation. Thus the incompressible cells do not have to do any work raising the fluid above them. The total buoyancy work remains Mgδh. The expansion work is zero, so the total work done by the rotation is Mgδh.
Let us return to the gas-filled cells depicted here. The buoyancy work consists of two components. The first component is the work done by cell B as it slides off cell A. This work is Mgδh, just as it is for an incompressible fluid. The second component is the work required lift the gas above the block.
When cell A rises, the combined height of the two left-hand cells increases by a small fraction of δh (the fraction is mgCvδh/pCp). The increase is small, but the weight of the gas that must be lifted is great (the weight is p). The work required to raise the upper gas is significant (the work is MgδhCv/Cp). After subtracting this work from the work done by cell B, we are left with a net buoyancy work of only MgδhR/Cp (for air, R/Cp is 0.29).
Unlike an incompressible cell, however, a gas cell does work as it expands. In Expansion Work we found that the warm, rising cell does MgδhCv/Cp more work as it expands than is required to compress the cold, falling cell. This expansion work turns out to be exactly equal to the work required to raise up the gas above the rotating block. When we add the buoyancy and expansion work together, we find that the total work done by the rotating cells is Mgδh, which is the same as the work done by the incompressible cells.
We see that buoyancy work and expansion work are separate sources of energy after all. In an incompressible fluid, we have only buoyancy work. The expansion work is zero. In a gas, we have both, but their sum is the same. This sum is what we call the impetus for circulation. Given a certain δh, the impetus for circulation is the same for both gas cells and incompressible cells. When the warm cell is taller by δh, the impetus for circulation is Mgδh.
In CC5, our calculation of buoyancy work ignored the work required to raise the upper gas, and so produced a value for buoyancy work that was incorrect, but equal to the impetus for circulation. Our calculation of expansion work, meanwhile, used Cp to multiply δT instead of Cv, and so produced a value for expansion work that was incorrect, but equal to the impetus for circulation. By accident, therefore, CC5 calculated the correct impetus for circulation in two different ways, and this was the origin of our mystery.
In our next post we will confirm today's argument by considering the enthalpy of incompressible and gas-filled cells. After that, we will return to enhancing our simulation, being confident that we understand the forces involved in the circulation of our atmospheric cells.

In other words, a cell of liquid at the bottom of a vessel, if is heated, expands because δV/δT = Vα is greater than zero and works on the surroundings and, becoming buoyant, rises. During the ascent the warm cell and the surrounding cold liquid have the same pressure but, as is δV/δp = 0 (the liquid is incompressible with respect to pressure) there is no longer expansion work and the surroundings gives back to the rising cell the geo gravitational energy obtained when the cell was heated. At the end the warm cell will reach the top of the liquid and, if is able to maintain its form, it will partially emerge until the level of the cold liquid will come back to its initial height. That is, the warm cell has a reactive exchange of geo gravitational energy with the cold liquid and eventually all the energy will remain to the warm cell.
ReplyDeleteConversely, a cell of gas, heated at the bottom, behaves as the cell of liquid, doing a greater work as its thermal dilatation is higher. During the ascent is now δV/δp = Rδ(T/p)/δp and the cell continues to expand until its temperature become equal to that of the surroundings, when it stops to rise. All the thermal energy given to the cell becomes geo gravitational energy of the surroundings.
The behavior of the liquid and the gas is fully different with regards to the energy transfer.
Michele
Dear Michele,
ReplyDeleteI'm glad to hear from you. I believe you are correct.
In order for convection to operate from bottom to top in a gas atmosphere, we must have temperature gradient dT/dz < −g/Cp. Otherwise the warm gas stops rising because it cools to the temperature of the surrounding air.
What I think I have demonstrated is that impetus for circulation exists, and that it does so for incompressible or compressible cells. The impetus does work accelerating the cells so that they will rotate, and it is the only work available to make them rotate. Given the mass of the cells and Newton's Second Law, we can calculate the minimum time it takes for the cells to perform the rotation.
Once the cells are moving, our simulation assumes they come to a stop, and if that's the case, their kinetic energy must turn into heat, which is why we allow the impetus for circulation to be divided into four parts and returned to the cells.
Yours, Kevan