Island Inversion

We invite you to download Circulating Cells, Version 8.4 by clicking here so that you can watch it simulate air movement above an island in the sea. Start the program and set it to Cycle mode with Q_sun set to 700 W/m². Download this file and read it into the simulation with the Load button. You will see the an island of sand at the center of the surface blocks, surrounded by water on the left and right. The saved state of the cell corresponds to midnight, so you can start the simulation right away.

Just before dawn, at solar time 5.5 hr, you will see that the temperature of the air resting upon the sand of the island is slightly cooler than the air above. The following figure is a close-up of the air above the sand, in which ran the program with max_T set to 300 K and min_T set to 260 K in the source code so as to make the cool layer more obvious. Note that the orange-lined surface blocks are sand and the blue-lined ones are water.



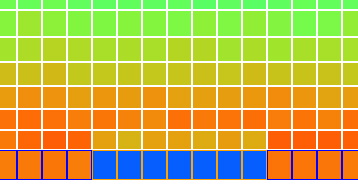
Our simulation produces the inversion of atmospheric temperature that we discussed in Surface Cooling, Part IV. In that post, we proposed that the leaves of a forest would cool at night by radiation. Air in contact with the leaves would descend to the ground and drag warmer air down from above. We suggested that this process might cool the first ten to a hundred meters of air above the treetops, producing temperature inversion. Perhaps that is indeed what happens over a forest. But in our simulation, whenever the surface is cooler than the air resting upon it, we set the heat transfer by convection and conduction to zero. How, then, does inversion occur over our simulated island?

The sandy island cools by roughly 50°C to −12°C at night. At this temperature, it radiates only 260 W/m². Of this, 130 W/m² is absorbed by the bottom layer of the atmosphere, because we have transparency fraction set to 0.5. Meanwhile, the bottom layer of our simulated atmosphere radiates heat both night and day. At the start of the night, its temperature is around 300 K and it radiates 230 W/m² to the sand below, which is half the heat a black body at that same temperature would radiate. By radiation alone, we see that the cells above the sand are losing 100 W/m².

The mass of our cells is 330 kg/m², and their heat capacity at constant pressure is 1 kJ/kg, so 100 W/m² will cool them by roughly 1°C/hr. This is what we see during the night above our island. Inversion does not occur over the water because the water surface in our simulation has ten times the heat capacity as the sand, and so cools ten times less at night. The water continues to warm the lower atmosphere with its radiation during the night. Thus we see how back-radiation and a surface with low heat capacity work together to produce temperature inversion.