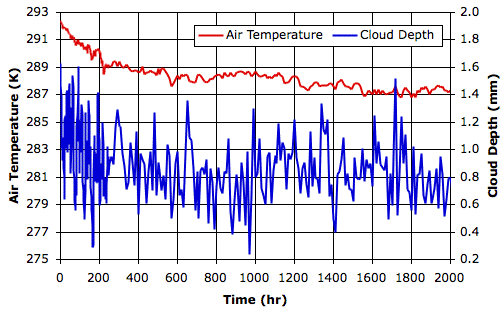
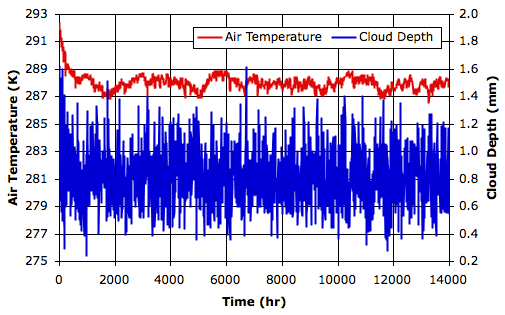
In the figure below, the blue graph shows temperature versus altitude for thermal equilibrium in the wet atmosphere of our Radiating Clouds simulation. We loaded the equilibrium state, RC_14000hr, into CC11 and instructed the simulation to print temperatures and altitudes.
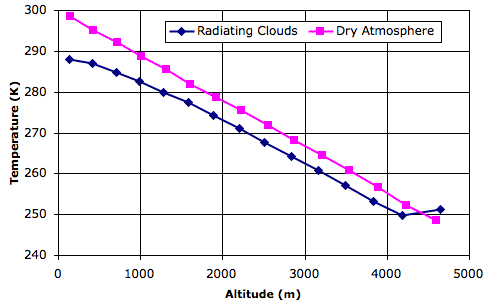
For comparison, we went back to Simulated Planet Surface and loaded the equilibrium state, Day_4, which arises with the same solar heat, but with the surface entirely made of sand. Thus the pink graph shows temperature versus altitude in a dry atmosphere.
The equilibrium state of the dry atmosphere, which looks like this, shows a linear drop in temperature with altitude. According to our calculations, this slope should be −g/Cp, where g is gravity and Cp is the specific heat capacity of the dry gas. Our simulation uses 10 N/kg for gravity and 1003 J/K for Cp, so the slope of the pink graph should be close to −0.010 K/m. Its actual slope is −0.011 K/m.
The equilibrium state of the wet atmosphere, which looks like this, shows a linear drop in temperature only between altitudes 2 km and 4 km. Near the surface of the planet, the heat liberated by condensing water vapor into rising air reduces the amount by which air cools as it rises. In the tropopause, radiation from the planet surface is absorbed by the tropopause clouds, causing them to be warmer than the air immediately below. In the linear region of the graph, the slope is −0.011 K/m, but if we simply divide the total drop in temperature by the altitude of the tropopause, we obtain a net slope of −0.008 K/m.
Looking at graphs such as these, it appears that the Earth's atmosphere has a lapse rate of around −0.0065 K/m. Our simulation does not come up with this lapse rate exactly, but we see that the introduction of water does cause a substantial reduction in the net lapse rate, and with this we are well-satisfied.
The average temperature of the surface of the Earth is around 14°C, or 287 K. This is the average temperature of the air just above the planet surface, not the temperature of the surface itself. The thermometers we use to measure the surface temperature are several meters above the ground. When we use dry air and a sandy surface in our simulation, the average temperature of the surface air is 298 K. But when we add radiating clouds, rain, and snow, the average temperature drops to 288 K, or 15°C. We are well-satisfied with this agreement also.