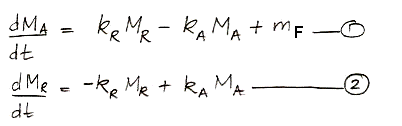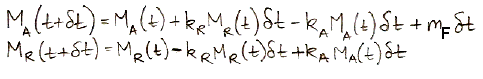Carbon Cycle: With Ten Petagrams per Year

Today we use our model of the Earth's carbon cycle to show us what will happen if we start adding ten petagrams of carbon to the atmosphere each year by burning fossil fuels. Ten petagrams is roughly the amount we emitted in 2015, so we are going to see how this addition would affect the concentration of CO2 in the atmosphere if it began suddenly, continued for thousands of years, and was the only phenomenon affecting change in the carbon cycle. In particular, our calculation assumes that the temperature of the atmosphere and the ocean remain constant, which may not be true if rising CO2 concentration enhances the greenhouse effect.

We begin with the carbon cycle in its natural, equilibrium state. The concentration of CO2 in the atmosphere is 300 ppm, which means it contains 650 Pg of carbon. The oceanic carbon reservoir, meanwhile, contains 77,000 Pg. Each year, the ocean emits 37 Pg into the atmosphere, and absorbs 37 Pg from the atmosphere. But now we start adding an extra 10 Pg/yr to the atmosphere by burning fossil fuels. In the the numerical equations that describe our carbon cycle, we set m_F = 10 Pg/yr. You can download our carbon cycle spreadsheet here. In it, you will find the following plot, along with our calculations.


Figure: Atmospheric and Oceanic Carbon Mass versus Time, with Ten Petagrams per Year Fossil Fuel Emissions. The time scale is logarithmic. Note that 1 Eg = 1,000 Pg. Click to enlarge.
During the first ten years, the total mass of carbon entering the atmosphere each year is 47 Pg/yr. But the mass absorbed by the oceans remains 37 Pg/yr. The mass of carbon in the atmosphere increases by 10 Pg/yr.

After ten years, we have emitted 100 Pg by burning fossil fuels. The mass of carbon in the atmosphere has increased by 80 Pg to 730 Pg. The rate at which carbon is absorbed by the ocean has increased in proportion, because there are more CO2 molecules available to absorb. The ocean now absorbs 41 Pg/yr. With 37 Pg/yr emitted by the ocean, and 10 Pg/yr emitted by burning fossil fuels, the carbon mass of the atmosphere increases by 6 Pg/yr.

After a hundred years, we have emitted 1,000 Pg by burning fossil fuels. The mass of carbon in the atmosphere has increased by 180 Pg to 830 Pg. The rate at which atmospheric carbon enters the oceanic reservoir is 47 Pg/yr. The mass of the oceanic reservoir itself has increased by 820 kg to 77,820 kg, which is only 1%. The rate at which oceanic carbon emerges into the atmosphere is still close to 37 Pg/yr. The atmosphere is in equilibrium: carbon enters at 47 Pg/yr and leaves at 47 Pg/yr. Its carbon mass increases only by 0.1 Pg/yr.

After one thousand years, the mass of carbon in the oceanic reservoir has increased by 13% to 87,000 Pg. The rate at which the ocean emits carbon into the atmosphere has increased by 13% to 42 Pg/yr. The mass of carbon in the atmosphere has risen to 910 Pg, and every year 52 Pg of atmospheric carbon is absorbed by the oceanic reservoir. The atmosphere is still in equilibrium with the ocean: each year 52 Pg enters and 52 Pg leaves. Its carbon mass continues to increase by only 0.1 Pg/yr, while the carbon in the oceanic reservoir increases by 10 Pg/yr.

After six thousand years, the mass of carbon in the atmosphere has doubled, and the mass in the oceanic reservoir has almost doubled. The plot below shows how atmospheric CO2 concentration increases with time for the same scenario.


Figure: Atmospheric CO2 Concentration in Response to Emission of 10 Pg/yr of Carbon by Burning Fossil Fuels. Units are parts per million by volume. Click to enlarge.
Burning fossil fuels at the rate we are going today, it would take 100 years to raise the concentration of CO2 in our natural, equilibrium atmosphere from 300 ppmv to 400 ppmv, and 6,000 years to raise it from 300 ppmv to 600 ppmv.

Carbon Cycle: Equations and Diagram

Suppose human beings start to add carbon to our natural, equilibrium atmosphere at a rate m_F by burning fossil fuels. We will express m_F in petagrams of carbon per year, or Pg/yr. Note that we have been working with carbon masses, not CO2 masses, but we can convert atmospheric carbon mass to atmospheric CO2 mass simply by multiplying by 3.7, which is the ratio of the molar mass of CO2 to the atomic mass of carbon-12. With the addition of m_F, our carbon cycle now looks like the diagram below. The time t = 0 yr is the moment just before we start we start adding m_F to the atmosphere.


Or, expressed as two differential equations, it looks like this:


We can solve these differential equations in the same way we already solved those of carbon-14 concentration. Examining the equations, we see that we can obtain the behavior of non-radioactive carbon by setting the decay constant, γ, to zero and inserting the the human emission of carbon in place of the cosmic ray creation of carbon-14. More convenient than the analytic solution for our purposes, however, is a numerical solution that we can implement in a spreadsheet and combine with the historical and projected values for m_F as our study progresses.

In the numerical solution, we pick a time step small enough that changes in the masses and transfer rates are negligible during the step. Suppose our step is δt. Provided δt is small enough, we can assume, for example, that m_A during each step is equal to k_A times the value of M_A at the beginning of the step. We do not have to account for the fact that M_A may be changing during the step, because the time step is so small these changes will be negligible compared to M_A. For our carbon cycle, it turns out that one year is always a small enough time step, and in long, slow developments, ten years is small enough.

The following equations are the numerical equivalents of our differential equations. They show how we calculate M_A and M_R at time t+δt using their values at time t.


The current rate at which humans emit carbon by burning fossil fuels is close to, 10 Pg/yr. In our next post, we will set m_F to a constant 10 Pg/yr and calculate how our natural, equilibrium atmosphere responds over ten thousand years.

PS. If you find our carbon cycle drawing too confusing and drab, you can try this one drawn by my youngest son.

Carbon Cycle: Rate of Transfer

Our study of the radioactive isotope carbon-14, which we began in Carbon-14: Origins and Reservoir, led us to the conclusion that roughly one in every eighteen atmospheric carbon atoms are absorbed by a vast oceanic reservoir each year. When the atmosphere and the reservoir are in equilibrium, the same amount of carbon flows out of the reservoir as into it, so that the mass of carbon in the atmosphere remains constant. But the oceanic reservoir contains over one hundred times as much carbon as the atmosphere.

We now embark upon a series of posts in which we calculate the effect of mankind's carbon emissions upon the atmospheric CO2 concentration. Our starting point for these calculations will be the natural, equilibrium atmosphere and oceans of the late nineteenth century. This atmosphere contains 300 ppmv CO2, which implies a total atmospheric carbon mass of 650 Pg (see here). The oceanic reservoir contains 77,000 Pg, and each year 37 Pg of carbon is exchanged between the atmosphere and the reservoir (see here).

As we showed in our previous post, the probability of an atmospheric carbon atom being transferred into the oceanic reservoir is independent of the number of carbon atoms in the atmosphere. The number of carbon atoms moving into the reservoir is equal to the total number of carbon atoms in the atmosphere divided by eighteen. If we have twice as many carbon atoms, the rate at which they move into the oceanic reservoir will double. If m_A is the mass of carbon moving into the reservoir every year, and M_A is the mass of carbon in the atmosphere, we must have:

m_A = k_AM_A, where k_A = 37 Pg/yr ÷ 650 Pg = 0.057 Pg/yr/Pg.

The probability of a carbon atom in the oceanic reservoir being released into the atmosphere is likewise independent of the number of carbon atoms in the reservoir. If m_R is the mass of carbon leaving the reservoir every year and M_R is the mass of carbon in the reservoir, we must have:

m_R = k_RM_R, where k_R = 37 Pg/yr ÷ 77,000 Pg = 0.00048 Pg/yr/Pg.

If we were to double suddenly the mass of carbon in the atmosphere, carbon would start to move into the oceanic reservoir at double the rate. The graph of atmospheric carbon dioxide concentration would look almost exactly like the graph of carbon-14 concentration after the nuclear bomb tests, which we present here. The movement of carbon between the atmosphere and the oceanic reservoir is governed by almost exactly the same equations as the movement of carbon-14. The only difference is that carbon-14 decays, while carbon-12 lasts forever.

UPDATE: The above calculations are consistent with Henry's Law of gasses dissolving in liquids. Henry's Law applies when the concentration of gas in the liquid has reached equilibrium at a particular temperature with the concentration of gas above the liquid. At equilibrium, the rate at which the liquid emits the gas is equal to the rate at which the liquid absorbs the gas. Henry's Law states that the equilibrium concentration of the gas in the liquid at a particular temperature is proportional to the partial pressure of the gas above the liquid. According to Boyle's Law, the partial pressure of a gas at a particular temperature is proportional to the number of gas molecules per unit volume. In our rate of transfer equations, the rate at which CO2 is absorbed by the ocean is proportional to the concentration of CO2 in the atmosphere, and the rate at which CO2 is emitted is proportional to the concentration in the liquid. If we double the concentration of CO2 in the atmosphere, our equations tell us that the rate of emission by the oceans will equal the rate of absorption only if the concentration of CO2 in the oceans also doubles, which is precisely what Henry's Law requires. Of course, we have not yet considered how changing the temperature of the atmosphere and ocean will affect the rates of transfer, but we will get to that later.

Carbon-14: Probability of Exchange

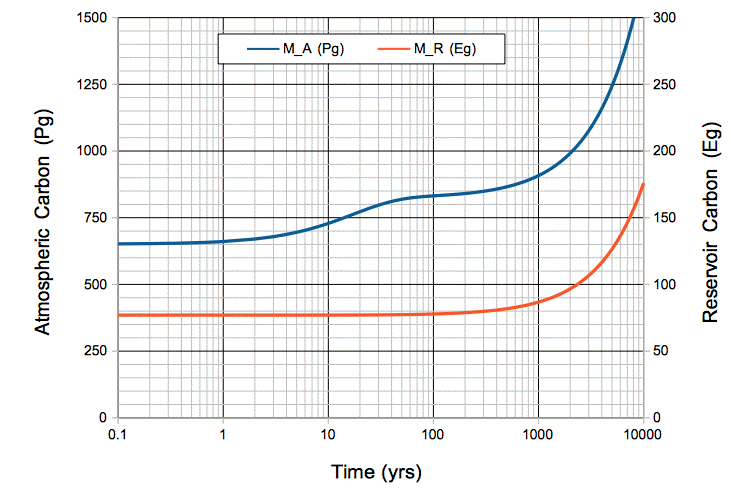
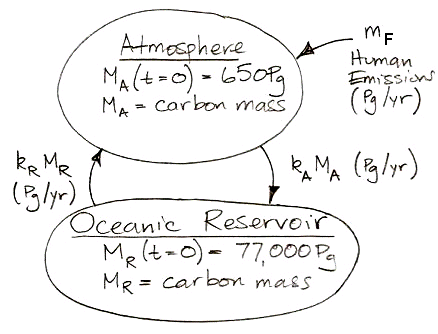
In the carbon cycle of our natural, equilibrium atmosphere, each carbon atom in the atmosphere has a certain probability each year of being absorbed by the reservoir. We call this the probability of exchange in the atmosphere. According to our calculations, 37 Pg of carbon is absorbed by the reservoir each year. Meanwhile, the total mass of carbon in the atmosphere is 650 Pg. To the first approximation, the probability of exchange in the atmosphere is 5.7% per year.

Likewise, a carbon atom in the reservoir has a probability of being released into the atmosphere each year. We have 37 Pg of carbon emerging from the reservoir each year, and the reservoir contains 77,000 Pg of carbon, so the probability of exchange for the reservoir is 0.048% per year.

Almost all carbon in the atmosphere is bound up in CO2. In our previous post we showed that the reservoir is the deep ocean. When a carbon atom enters the deep ocean, it does so as part of a CO2 molecule. The CO2 molecule arrives by chance at the ocean surface, and by further chance it dissolves into the salty water. The CO2 molecule turns into some kind of carbonate ion. This ion mixes down through the top thousand meters of water until it reaches the deep ocean. The carbon atom is now part of the reservoir. The probability of this happening each year is 5.7% for each and every CO2 molecule in the atmosphere.

Likewise, the probability of any carbon atom in the reservoir emerging into the atmosphere as part of a new CO2 molecule each year is 0.048%. The molecule or ion containing the carbon atom mixes up through the top one thousand meters of the ocean, arrives by chance at the surface, and by further chance emerges from the surface as an atmospheric CO2 molecule. (See UPDATE below for discussion of ocean chemistry.)

The exchange of carbon between the atmosphere and the ocean is a first-order chemical process. During the process, each carbon atom is acting alone. It does not require the cooperation of any catalyst to permit it to be dissolved in saltwater or released from saltwater. If we were to double the number of CO2 molecules in the atmosphere, so that six hundred out of every million air molecules were CO2 instead of only three hundred, the probability of any one of them being absorbed by the reservoir each year would remain the same.

If the reservoir were something more complex than the ocean, such as a forest, we would be unable to assert that the probability of exchange was unaffected by the number of CO2 molecules in the atmosphere. A forest needs water and sunlight to convert CO2 into sugar and oxygen. If we double the number of CO2 molecules in the atmosphere, we might find that CO2 molecules are lining up inside forest leaves waiting for enough water and sunlight to arrive before they are turned into plant matter. But our reservoir is the ocean, and entering and leaving it is a statistical process in which each carbon atom acts in isolation.

So far, we have assumed that the atmosphere and reservoir are staying at the same temperature. They could be at different temperatures, but they are neither warming nor cooling. But we note that the probability of exchange is strongly affected by temperature. We have only to look at the decreasing solubility of CO2 in water with temperature, as presented here, to see that this strong effect must exist.

For now, we assume our natural, equilibrium atmosphere, and its carbon reservoir, are neither cooling nor warming. The probability of exchange in the atmosphere remains constant at 5.7% per year, even if we halve or double the atmosphere's CO2 concentration. The probability of exchange in the reservoir remains constant at 0.048% per year, even if the mass of carbon in the reservoir halves or doubles. The probability of exchange is independent of concentration.

This concludes our series of posts on carbon-14. In our upcoming posts, we will apply what carbon-14 has taught us about the Earth's carbon cycle to predict how human CO2 emissions will affect the CO2 concentration of the atmosphere.

UPDATE [08-NOV-16]: In many gas-liquid systems, changes in concentration or acidity can change the probability of emission for a dissolved gas molecule. This variation in probability is possible when the dissolved gas appears as several species in the liquid, some of which cannot emit a gas molecule, while others can. When the relative concentrations of these species changes, the probability of a dissolved gas molecule being emitted also changes. For example, if a gas dissolves into two species A and B in equal proportion, and A has a 10% per year probability of emission while B has a 0% probability, the average probability is 5% per year. If we add acid to the system and the ratio of the two becomes 75% A and 25% B, the probability of emission for each species remains the same, but the average probability rises to 7.5% per year. Our carbon-cycle model is based upon the assumption that the atmosphere-ocean system does not exhibit concentration-dependent nor acidity-dependent probability of emission. Let us justify our assumption with a brief discussion of ocean chemistry.

The top layer of the ocean is saturated with calcium carbonate (CaCO3). The CaCO3 co-exists with the carbonate ions created by CO2 dissolved in water. In Figure 5.6 of Carbonate Equilibria we see the pH of a liquid saturated with calcium carbonate is around 8.5 (log of the H⁺ concentration is −8.5) for CO2 partial pressure of 300 ppmv (log of CO2 partial pressure is −3.5). The pH of our contemporary ocean is around 8.2, while the pH of a system of only CO2 and water is around 5.8. Continuing with Figure 5.6, for CO2 partial pressures in the range 100 ppmv to 10,000 ppmv (log of CO2 partial pressure is −4 to −2) the carbon content of the solution is dominated by HCO3⁻. The concentration of HCO3⁻ increases in proportion to the partial pressure of CO2 (its slope is 1.0 in the log-log plot). The concentration of HCO3⁻ is 2.0 times that of Ca²⁺ throughout the range 100 ppmv to 10,000 ppmv (see Table 5.1 Case 2 for numerical values). As we increase the partial pressure of CO2, an equal number of of CaCO3 and CO2 molecules dissolve. Each CaCO3 molecule that dissolves adds one Ca²⁺ ion, one HCO3⁻ ion, and one OH⁻ ion to the solution. Each CO2 molecule that dissolves contributes one HCO3⁻ ion and one H⁺ ion. The OH⁻ and H⁺ ions combine to form H2O, leaving the other ions in solution. The HCO3⁻ concentration, the dissolved CO2 concentration, and the dissolved CaCO3 concentration all increase in proportion to the partial pressure of CO2. As seawater changes temperature and pressure, the saturation concentration of CaCO3 changes, and CaCO3 can precipitate, as it does in the Persian Gulf, staining the water white.

When a gas and liquid are at equilibrium, there is as much gas entering the liquid per unit time as there is leaving it. Because gaseous CO2 has only one species, its probability of absorption into the ocean does not vary with its concentration. When we double the concentration of atmospheric CO2 from 300 ppmv to 600 ppmv, we double the rate at which it enters the ocean. When the ocean attains a new equilibrium with the 600-ppmv CO2 atmosphere, the rate at which CO2 is emitted by the ocean must be double the rate for 300 ppmv. At the same time, using the CaCO3-CO2-water system as our guide, we see that the concentration of dissolved CO2 will double for this doubling of atmospheric concentration. The doubling of dissolved concentration combined with the doubling of emission tells us that the probability of emission for CO2 molecules in the ocean is constant from 300 ppmv to 600 ppmv.

Another way to model the atmosphere-ocean system is to ignore the calcium carbonate and instead use a CO2-water system with added OH⁻, such as might come from mixing NaOH with the water. We add OH⁻ in order to increase the pH of the system from 5.8, which applies to the CO2-water system alone, to 8.2, which applies to the ocean. This OH-CO2-water system exhibits more complex behavior in the range 100 ppmv to 1000 ppmv than the CaCO3-CO2-water system. The dissolved CO2 concentration does not increase in proportion to the atmospheric concentration. So far as we can tell, this OH-CO2-water model is what climate scientists are using when they conclude that the ocean will not absorb our CO2 emissions in proportion to atmospheric CO2 concentration. They express its non-linear behavior with a number they call the Revelle Factor. We do not understand why they prefer an OH-CO2-water model to the CaCO3-CO2-water model, nor have we seen in the climate science literature any plots like those of Figure 5.4 or Figure 5.6 for an OH-CO2-water system. The closest we have seen any promoter of the Revelle Factor come to plotting such graphs is here, but that author had no explanation for why they used the OH-CO2-water system instead of the CaCO3-CO2-water system.