Extended Atmospheric Absorption Spectra

In our previous post we concluded that we needed to extend our existing absorption spectra to cover the range 5 μm to 60 μm. So we returned to the Spectral Calculator and, entered our gas properties for each atmospheric layer, and obtained the absorption spectra from 30 μm to 60 μm. We added these to our existing spectra and obtained the following graph (click for a larger version).



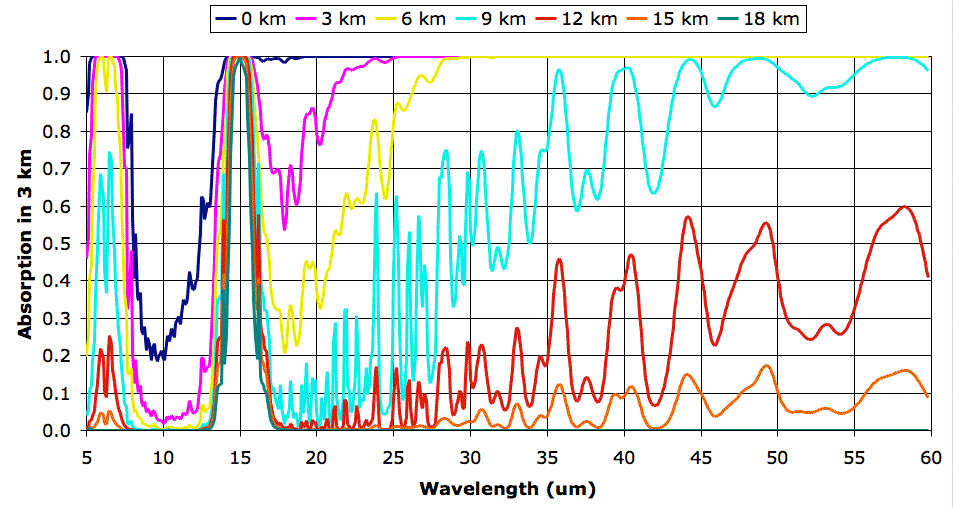
As a point of detail, each spectrum we receive from the Spectral Calculator contain tens of thousands of values. We condense the spectra using a program that calculates the average absorption in each 0.1-μm window. The result is a spectrum with a point every tenth of a micron. You will find the original spectra in our data archive, in the EA_1 folder. You will find the condensed spectra here. The condensed file can act as input to our climate models and is convenient for generating plots like the one above.

We apply our total escaping power program to our extended spectra and obtain the following values for power per square meter. For an explanation of the various columns, see here.

------------------------------------------------
      Name    Temp       BB     Layer   Escaping
------------------------------------------------
   Surface    290.0    401.1    388.8     89.8
      0-km    280.0    348.5    262.6     58.9
      3-km    270.0    301.3    184.8     49.7
      6-km    250.0    221.5    111.5     51.4
      9-km    230.0    158.7     50.7     29.4
     12-km    220.0    132.8     22.2     11.2
     15-km    220.0    132.8     14.4      5.5
------------------------------------------------
Total:                                   296.0
------------------------------------------------

Let's look at the first line of numbers, which apply to the surface of the Earth. We treat the surface as a black body, as we justify elsewhere. Using Stefan's Law we find that a black body at 290 K (that's 17°C) should radiate 401.1 W/m². Our calculator adds the power radiated in each 0.1-μm window from 5 μm to 60 μm, in a process we call numerical integration, and arrives at 388.8 W/m². That's closer to 401.1 W/m² than the 349.0 W/m² we obtained when we our calculation extended only to 30 μm. But we still have a difference of 12.3 W/m².

We experiment with the black-body radiation spectrum using this program. When we integrate in 0.1-μm steps all the way from 1 μm to 300 μm, we get a total power of 401.0 W/m², which is almost exactly what we obtain from Stefan's Law. We use our program to determine the power radiated by a black body at various wavelengths.

--------------------------
Range (um)  Power (W/m^2)
--------------------------
0.1-1          0.0
1-5            3.8
5-60         388.8
60-100         6.4
100-200        1.8
200-300        0.2
--------------------------
Total        401.0
--------------------------

We have a total of 12.2 W outside the 5-60 μm range of our absorption spectra. In the future, perhaps we will extend our spectra to include this missing 3%, but for now we are content with our omission. Furthermore, we are satisfied that our numerical integration in 0.1-μm steps, which is the basis of our climate model's calculations, is accurate to better than 0.1%.

Our next step is to generate a new set of spectra for the atmosphere with 660 ppm CO2, and see how the total escaping power changes. Our guess is that the total escaping power will decrease, but we are not sure by how much.