Adiabatic Magic

A while back, a visitor here tried to persuade us that heat flow through an atmosphere was not required to make it warmer at the bottom than the top. He was convinced that adiabatic circulation would always take place within the atmosphere, regardless of whether or not heat was flowing, and this circulation would always make the bottom warmer than the top. At Science of Doom, meanwhile, several authors try to convince us that the surface of Venus will be super-hot even if it is not being heated by the Sun. They describe some kind of adiabatic process, which we will call adiabatic magic, by which any atmosphere will always be warmer at the bottom than the top, even with no heat flow. Indeed, one author goes so far as to say that heat flow from bottom to top will actually decrease the temperature difference between the lower and upper atmosphere.

We are well aware that air taking part in atmospheric convection will cool down as it rises, and warm up as it falls, but this circulation is powered by heat absorbed from the planet and subsequently radiated into space by the atmosphere. It is not spontaneous or self-generated. The circulation requires that the planet surface be warmed by the sun and that the atmosphere be capable of radiating heat into space at higher altitudes. With no heat flow, there will be no circulation, and no temperature difference between top and the bottom of the atmosphere. In other words: there is no such thing as adiabatic magic, as we will now demonstrate.

The diagram below shows how we can use adiabatic magic to create a machine that is 100% efficient at turning heat into work. Such a machine is also known as a perpetual motion machine of the second kind.



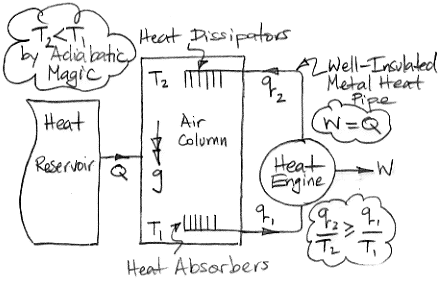
In the center of the diagram is an air column. The action of gravity is indicated by the double-headed arrow with the letter g. The column is high enough that the weight of the air it contains causes the pressure to be greater at the bottom than the top. By adiabatic magic, the bottom of the column is hotter than the top, so T₁ > T₂. We exploit this temperature difference with a heat engine. Metal veins absorb heat from the air at base of the column. A metal rod, well-clad with thermal insulation, carries this heat to a heat engine. A heat engine is something like a steam turbine, which exploits the flow of heat from hot to cold in order to generate work. Heat flows out of the engine through another metal rod to top of the column. The heat flowing into the engine is q₁ and the heat flowing out is q₂. The work produced by the heat engine is W. We express the heat flow and work output in Watts.

The First Law of Thermodynamics requires that W = q₁ − q₂. The Second Law of Thermodynamics requires that the entropy of the heat going in must be less than or equal to the entropy of the heat going out. With the absolute temperature scale, this means that q₁ / T₁ ≤ q₂ / T₂. Subject to these constraints, we see that our heat engine can produce work by exploiting the temperature difference between the bottom and the top of the air column.

Of course, we are taking more heat out of the bottom of the column than we are restoring to the top, so the total heat of the column will tend to decrease. We're not sure what the adiabatic magic theory has to say about an air column as it cools, so we are going to avoid this issue by adding heat to the column from a large reservoir. We add exactly as much heat as the column is losing by the action of the heat engine. The heat we add is Q, so Q = q₁ − q₂ = W.

So now let us consider the air column and the heat engine acting together. They constitute a perpetual motion machine. We see that we have Q entering the machine and W leaving. The machine turns heat into work with 100% efficiency. It is a perpetual motion machine of the second kind.

The adiabatic magic idea is one of a class of impossible ideas: those that propose the spontaneous separation of heat into hot and cold. The above diagram could be adapted to disprove any such idea with equal facility. If someone claimed they had invented a new material that always became hotter at one end than the other, even with no heat flow from one end to the other, we could disprove his claim with the above diagram.

Because adiabatic magic is impossible, we see that a transparent atmosphere can be no warmer at the bottom than at the top. Transparent gas cannot radiate heat into space (see Radiative Symmetry). In the case of Venus, if nothing heats the surface, the gas at the surface will be no warmer than the gas at the altitude to which sunlight does penetrate.

Of course, our atmosphere does radiate heat into space, so the lower air is warmer than the upper air, in order to transport that heat. And Venus's atmosphere gets hotter all the way to the surface, which means it is transporting heat away from the surface and radiating it into space.

Condensation and Convection

One of our readers has been asking me about the role of condensation in accelerating convection, as described in papers like this one. So let us dicsuss the effect of evaporation and condensation in convection.

Consider a kilogram of air that has just been warmed at the surface of the Earth, and is now rising towards the tropopause as part of atmospheric convection. This kilogram has temperature 300 K, pressure 100 kPa, and volume 860 l (liters). Let us suppose this air contains 10 l of water vapor. This water vapor has mass 10 g and would occupy 10 ml (milliliters) if it condensed into liquid.

Our rising volume of air expands and cools. Its pressure drops to 50 kPa and its temperature to 250 K. It expands to 1400 l. At this temperature, almost all of our water must condense into liquid. Before condensation, the water occupies 14 l. When it condenses it will turn into microscopic water droplets that occupy only 14 ml. Of course, these droplets will freeze afterwards, but let's ignore that for now, and consider what happens when the water first condenses.

Most likely, the condensation will occur gradually as the air expands, but we will imagine that it happens after the expansion is complete, so we can calculate the net effect of condensation upon the pressure of our gas. At the end of the expansion, our air contains supersaturated water vapor, like the gas in a cloud chamber.

Consider the first gram of water that condenses. Let us assume, for the time being, that this condensation happens instantly, so that our two cubic meters of air has no time to expand or contract during the process. That is to say: we assume the condensation takes place at constant volume.

Before condensation, this one gram occupied 1.4 l in our volume of 1400 l. After condensation, the water droplets occupy a combined volume of only 1 ml. The remaining air and water vapor expand into our 1400 l. As it expands, its pressure decreases by 0.1%.

When water condenses, it gives up its latent heat of evaporation, which is 2 MJ/kg. When the first gram of water condenses, it gives up 2 kJ of heat to our 1400 l of air. The heat capacity of air at constant volume is roughly 700 kJ/kgK, so our kilogram of air warms up by around 3 K. It's pressure increases by 3 K ÷ 250 K = 1.2%.

We see that the first gram of water condensation causes a net increase in pressure of 1.2% - 0.1% = 1.1% in our kilogram of air. Suppose the air all around is dry. It has not been warmed by condensation. It's pressure has not increased. Our two cubic meters pushes outwards with its greater pressure and expands until it's pressure is the same as that of the surrounding air. It will expand by 1.1%. Its 1 kg of mass will occupy the same volume as 1.011 kg of surrounding dry air. It will experience an upward buoyancy force of 11 g weight, or 0.11 N. This force will cause it to accelerate upwards at 0.11 m/s². Within less than a minute, it will be traveling upwards at a few meters per second. At that point, other forces will come into play to slow it down. We note that we allowed only 1 g of our water vapor to condense. If all 10 g condensed at once, our kilogram of air would experience ten times more lift.

We see that condensation does indeed cause air to rise more quickly than surrounding dry air.

Moist air will expand more than dry air as it rises towards the tropopause. Evaporation, on the other hand, causes air to rise more slowly. Air at the surface of a dry desert heats up fast in contact with the hot sand. It rises quickly. We get dust devils and sand storms. But air on the surface of the ocean does not heat up quickly. Water evaporates from the ocean, cooling the ocean surface and the air, so that the air lingers above the ocean, accumulating more and more water vapor. Eventually, the air will rise, if only because it becomes saturated with water vapor. But we see that water rising from the ocean is not as hot compared to the air above it as is air rising from the desert. The initial rise will be slow compared to the rise over a desert. But if the water starts to condense out of the moist air, and the moist air is surrounded by dry air, the moist air will begin to rise more quickly, sucking more moist air up beneath it.

Thus we expect low-altitude storms over a desert and high-altitude storms over an ocean.

PS. Another writer concludes that the upward force on a cubic yard of air due to condensation will be close to a thousand pounds. He says, "I’m not intending to do the calculations any further here, because it is basic knowledge." Had he performed the calculations, he would have discovered that the effect of water vapor contraction is opposite to his claims (the contraction tends to make the air more dense and therefore sink, while he claimed that the contraction decreases pressure and therefore creates lift) and that his forces were off by four orders of magnitude (the net lift is of order 0.1 pounds per cubic yard, not 700 pounds per cubic yard).

PPS: The debate on this subject continues over at Watt's Up With That?.

PPS. Look in the comments for an explanation of evaporation and condensation on a molecular level.

Venus

UPDATE: Initial version of this post used diatomic gas equation for the compression of CO2. Have now corrected this oversight, and find that our estimate of Venus's surface temperature is much improved.

One of our readers suggested we consider the atmosphere of Venus. What a good idea. Let's see how well we can estimate Venus's surface temperature using our understanding of atmospheric convection and the greenhouse effect.

According to Wikipedia, Venus's tropopause is at an altitude of 65 km with temperature 243 K (−30°C) and pressure 10 kPa. The surface pressure, meanwhile, is almost a thousand times greater: 9,300 kPa, which is ninety-three times the surface pressure on Earth. Venus's atmosphere is made up almost entirely of CO2, but also contains 150 ppm of SO2 (sulfur dioxide), and this SO2 condenses into liquid droplets so that the atmosphere below the tropopause is filled with pale yellow clouds.

Venus reflects 90% of incident sunlight (it's Bond Albedo is 0.90). The remaining 10% is absorbed. We're not sure what fraction of the Sun's light reaches the surface of Venus, but our guess is 1%. The SO2 clouds refract and reflect light like our own clouds, but SO2 is a pale yellow liquid, not a clear liquid, and will absorb sunlight eventually.

According to Schriver et al., even a 0.5-μm film of SO2 ice will absorb over 20% of long-wave radiation, so a 10-μm droplet of SO2 liquid will absorb it all. The clouds of Venus are near-perfect absorbers of long-wave radiation, and near-perfect radiators too, just like our own water clouds. Unlike the Earth, however, Venus is always entirely covered with clouds. Neither the planet surface nor the lower atmosphere has any opportunity to radiate heat directly into space. Venus radiates heat directly into space only from its cloud-tops and upper atmosphere.

Although most of the sun's heat is reflected back into space, 10% is absorbed, and we estimate that around 1% reaches the surface of the planet. This heat will raise the temperature of the surface until it forces convection. Here is the convection diagram from our Atmospheric Convection post.



Gas warms at the surface. It rises, expands, radiates heat into space, falls, contracts, and warms again. As the gas expands, it gets cooler. As it contracts, it gets warmer. In our simplistic analysis, we assumed that the expansion and contraction were adiabatic, meaning they took place without any heat entering or leaving the gas. In reality, the gas radiates heat to nearby gas, absorbs heat from nearby gas, mixes with nearby gas, and generates heat through viscous friction. But our adiabatic assumption allowed us to estimate the temperature changes using the equation of adiabatic expansion and contraction. For an ideal diatomic gas, such as N2 or O2, p^−0.4T^1.4 remains constant during adiabatic changes, where p is pressure and T is temperature. For CO2, however, the equation is p^−0.3T^1.3 at 300 K and p^−0.2T^1.2 at 1300 K (see here for thermodynamic properties of CO2).

The Earth's tropopause is at altitude 15 km. According to our typical conditions, the tropopause is at 220 K with pressure 22 kPa, while the surface pressure is 100 kPa. Adiabatic compression implies that air descending from the tropopause to the surface will heat up to 340 K. But the Earth's surface is at only 280 K. Air descending 10 km from the tropopause to the surface appears to lose 20% of its heat while contracting to a third of its original volume.

The atmosphere of Venus will heat up as it descends from the tropopause to the surface, and it will be hottest if it does not lose any heat on the way down. The pressure rises from 10 kPa in the tropopause to 9,300 kPa at the surface. The temperature starts at 240 K. Adiabatic compression of an ideal diatomic gas would heat the gas to 1700 K. If we use p^−0.25T^1.25 as an approximation for CO2, we estimate a final temperature of 941 K.

According to Wikipedia, the surface temperature of Venus is actually 740 K. Carbon dioxide falling 65 km from the tropopause to the surface appears to lose 20% of its heat while being compressed into less than a hundredth of its original volume.

Despite the 20% difference between our calculations and our observations, we see that atmospheric convection makes the surface of Venus incredibly hot while leaving the surface of the Earth delightfully temperate.

If we recall our post on work by convection and another on atmospheric dissipation, we see that a strong convection cycle causes powerful weather. Venus's convection cycle produces an order of magnitude more contraction and expansion than the Earth's. We expect Venus's weather to be an order of magnitude more extreme. And indeed it is.