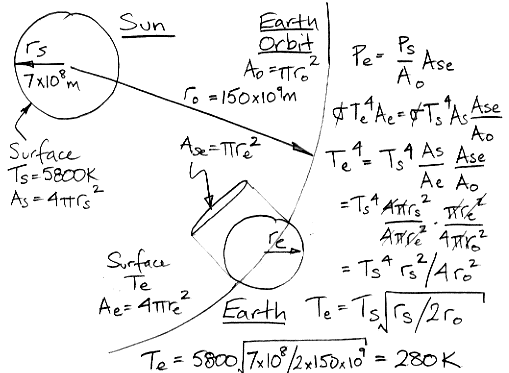
The Earth orbits the Sun at 150,000,000 km and has radius of 6,400 km. It presents a circular area to the Sun's radiation of 1.3×1014m2 . When it reaches the Earth, the Sun's radiation is spread out across a sphere of the same radius as the Earth's orbit, and so has intensity 1.4 kW/m2. The solar heat absorbed by the earth is 1.8×1017W.
Suppose the Earth itself were a black body. As a black body, it absorbs all heat landing upon it from the Sun. Either it radiates all this heat into space or it doesn't. If it doesn't, it gets warmer. If it gets warmer, it will radiate more heat, according to Stefan's Law. The Earth will eventually get warm enough that it radiates all the heat it absorbs from the Sun. We assume the Earth has already been through this warming process, and is radiating as much heat into space as it receives from the Sun.
The surface area of the Earth is 5.1×1014m2. If the Earth were a black body, it would radiate the solar heat it absorbs when it was at 280 K, or 7°C. In our diagram, we show how all terms in our calculation cancel out, except for the temperature of the Sun, Ts, the radius of the Sun, rs, and the radius of the Earth's orbit, ro, resulting in a simple formula. Using this formula, we also arrive at 280 K for the Earth's radiating surface temperature.
As it is, the average temperature of the Earth's surface is 287 K, or 14°C. At first glance, the Earth appears to behave like a black body. But is it really?
ASIDE: The Sun delivers 1.8×1017W to the Earth, and the Earth's surface area is 5.1×1014m2, so the average power received from the sun at the Earth's surface is 350 W/m2. (Well, its 353 W/m2 with our numbers, but we have rounded to two significant figures.)

Goodd reading this post
ReplyDeleteHi Kevan,
ReplyDeleteAfter reading through some of the fantastic science in this blog I had the idea of including the emissivity of the earth in the calculations for the earths theoretical temperature.
According to wikipedia the emissivity of the earth is approximately 0.95. (https://en.wikipedia.org/wiki/Emissivity#Emissivities_of_planet_Earth)
After taking this into account the temperature of the earth is 286.15ºK or 13ºc, this is remarkably close to the 14/15ºc average global temperature.
If the emissivity of water is instead used (taken as 0.96) the temperature of the earth is calculated to be 285.40ºK or 12.25ºc, this is still close to the 14/15ºc average.
Kind Regards
Thomas
Hi Thomas, Thanks for your calculation. Did you use the same 0.95 for emissivity and absorptivity? I think you assumed the same absorptivity and 5% drop in emissivity, so you would need to increase radiation from the Earth by 5%, which for a 4th order power law would require a 1.25% increase in absolute surface temperature, from 280 K to 283.5 K. You get 285.4 K. What am I missing? Best, Kevan
ReplyDeleteHi Kevan,
ReplyDeleteThanks for the reply, I think I see the discrepancy, I have used 4 significant figures for the radius of the sun, taking it to be 6.975x10^8 m instead of 7x10^8 m, and 3 significant figures for the orbital radius of the earth, taking it to be 147x10^9 m instead of 150x10^9 m, this has caused the discrepancy in results.
Using more significant figures gives a result of 282.50ºK for an emissivity of 1.0.
Method:
Following your calculations I added emissivity at the start to the term calculating the power received. This results in the final equation: T(Earth) = T(sun) * 1/(4th root(E)) * (sqrt( r(sun) / r(orbit) )
Yielding the result of 286.15ºK for an emissivity of 0.95.
Another method I tried is using the Stefan-Boltzmann law directly,
The intensity of radiation received by the earth is constant and equal to the intensity of radiation emitted by the earth, now the intensity of radiation received is known and is approximately 342Wm^-2,
as M = E*o*T^4
Therefore T = 4th root (M / ( E * o) )
Where T is temperature (K) , M is the intensity of radiation (Wm^-2), E is the emissivity, o is the Stefan-Boltzmann constant (Wm^-2K^-4).
Solving for the temperature of the earth with an emissivity of 1.0 we get a temperature of 278.68ºK, and with an emissivity of 0.95 I get a temperature of 282.28ºK
Let me know what you think.
Kind Regards
Thomas Lee
Your calculations look good to me. With received radiation constant, and emissivity dropping by 5%, you see a 1.29% increase in absolute temperature at the surface of the Earth. Meanwhile, 1/sqrt(sqrt(0.95)) = 1.0129. My guess above was inaccurate in that I used 1.0125 as an approximation.
ReplyDeleteIn our later work here, where we perform a simulation of clouds forming and radiating into space, the simulation produces an average cloud cover. From that we could estimate the absorptivity of the Earth for short-wave radiation. But let's suppose cloud cover is 30% on average, then we would have absorptivity of around 0.7. As to radiation, the clouds have emissivity 1.0 at long wavelength, but they are colder than the Earth's surface by around 0.6°C/100 m altitude. So that makes things more complicated.
Nevertheless, our simple calculation is close to correct, which is neat.