The greenhouse effect occurs when a planet's atmosphere is transparent to short-wave radiation arriving from its sun, but opaque to long-wave radiation emitted by the planet itself. Gases that bestow these properties upon an atmosphere are called greenhouse gases. So far, we have explored the greenhouse effect in the context of hypothetical examples such as our Extreme Greenhouse and Planetary Greenhouse.
In a planetary greenhouse, the lower atmosphere absorbs long-wave radiation. But the ability of any substance to absorb radiation is exactly matched by its ability to emit radiation. Thus the lower atmosphere emits long-wave radiation with the same efficiency that it absorbs long-wave radiation. Furthermore, although the lower atmosphere is opaque to long-wave radiation, the atmosphere gets progressively thinner as we ascend, so we are sure to come to an altitude where the atmosphere is so thin that it is transparent. Thus the middle atmosphere radiates heat out into space through the thin, upper atmosphere. The amount of heat the middle atmosphere radiates into space is proportional to the fourth power of its absolute temperature. The middle atmosphere will cool down until it radiates into space no more heat than it gains from the planet surface.
Greenhouse gases give rise to atmospheric convection. Gas in the middle atmosphere radiates heat into space and cools down. It contracts as it cools down, and becomes more dense. It sinks towards the planet surface. As it sinks, the surrounding atmosphere compresses it, causing it to warm up. But the sinking gas remains marginally cooler than the surrounding atmosphere, and so it continues to sink. When it reaches the planet surface, it stops sinking. The planet surface warms it up. Once it is warm enough, it becomes less dense and rises. As it rises, it compresses the surrounding atmosphere, and so cools down. But the rising gas remains marginally warmer than the surrounding atmosphere, and so it continues to rise. When it reaches the middle atmosphere, it starts to radiate heat into space. It cools down. The top of this convection cycle is the altitude at which the atmosphere stops cooling. We call it this altitude the tropopause.
In Work by Convection we showed that atmospheric convection generates power. This power causes the weather. Powerful weather is a feature of the greenhouse effect. The powerful weather extends only up to the tropopause, which is the upper extent of the convection cycle.
Atmospheric convection transports heat from the planet surface to the tropopause. But the amount of heat the convection cycle transports has very little effect upon the temperature drop from the bottom to the top of the cycle. Instead, it is the ratio of the pressure at the bottom to the pressure at the top that determines the temperature drop. An understanding of convection allows us to use the equations for adiabatic compression to calculate the warming caused by the greenhouse effect. If, for example, the pressure in the tropopause 30 kPa and the temperature is 210 K (−63°C), while the pressure at the surface is 100 kPa, then the temperature at the surface must be close to 300 K (27°C).
The temperature of the tropopause itself is, however, determined by the amount of heat it must radiate into space. The amount of heat it must radiate is determined by the manner in which the atmosphere absorbs long-wave radiation. We have considered a transparent atmosphere, an atmosphere that is opaque to all long-wave radiation, and an atmosphere that is transparent to some long-wave radiation but opaque otherwise. In more recent posts, we have considered the long-wave absorption spectra of water vapor and carbon dioxide. We found that doubling the concentration of a trace greenhouse gas causes progressively smaller increases in surface temperature.
So far, we have ignored the effect of clouds. Clouds have a strong effect upon the Earth's climate. They are made up of tiny water droplets, and are opaque to all long-wave radiation. At the same time, they reflect all short-wave radiation from the sun. Roughly a third of the Earth's surface is covered by clouds at any one time, and they reflect roughly a third of the Sun's radiation back into space, which tends to lower the temperature of the surface. But clouds block some surface radiation from reaching outer space, which tends to raise the surface temperature.
We are going to ignore clouds for now, but we will consider them in detail eventually. We are building up our understanding of the Earth's greenhouse effect one step at a time. In our next post, we will consider the absorption spectra of carbon dioxide and water vapor as they occur together in various layers of the Earth's atmosphere. We will obtain our spectra with the help of astronomy's Spectral Calculator.
Thursday, June 24, 2010
Thursday, June 17, 2010
CO2 Continuum
In CO2 Spectrum we present the absorption spectrum of pure CO2. In Water Vapor Continuum we suggested that we might be able to calculate the absorption spectrum of CO2 mixed with air by dividing the absorption spectrum of pure CO2 by the concentration of CO2 in the air. If the absorption length of 20-μm radiation in pure CO2 is 1 m, the absorption length in air with 0.033% CO2 would be 3 km. Such a calculation assumes that absorption takes place entirely within individual CO2 molecules, and is unaffected by interactions with other molecules.
In Water Vapor Continuum we found that a simple scaling of absorption with concentration is grossly inaccurate for water vapor. In Earth Radiator we showed that a 1-mm layer of water absorbs over 99.9% of all long-wave radiation. The graphs we present in Continuum Absorption Length imply that the same amount of water dispersed in a 1-km column of air will absorb less than 10% of long-wave radiation.
It turns out that a simple scaling calculation does not apply to CO2 either. If the absorption length of 20-μm radiation were 3 km in air with 330 ppm CO2, the Earth's atmosphere would be opaque to 20-μm radiation. But according to this popular graph, the CO2 in the Earth's atmosphere is transparent to 20 μm radiation.
In Absorption Line Broadening in the Infrared by Burch et al, we see how the presence of nearby molecules of all gases broadens the sharp absorption lines of the CO2 molecule. With high enough pressure, these lines become so broad that they overlap, and we see absorption of long-wave radiation at all frequencies within certain ranges, such as 13 μm to 17 μm.
We concluded that calculating the absorption spectra of water vapor and CO2 was far too big a project for us to embark upon. So we paid for a month's subscription to the most excellent Spectral Calculator. We asked the calculator to plot absorption by dry air with 330 ppm CO2 at 300 K and 1 atmosphere over a path length of 1 km. The calculator produced the following graph. For a logarithmic plot of the same data see here.
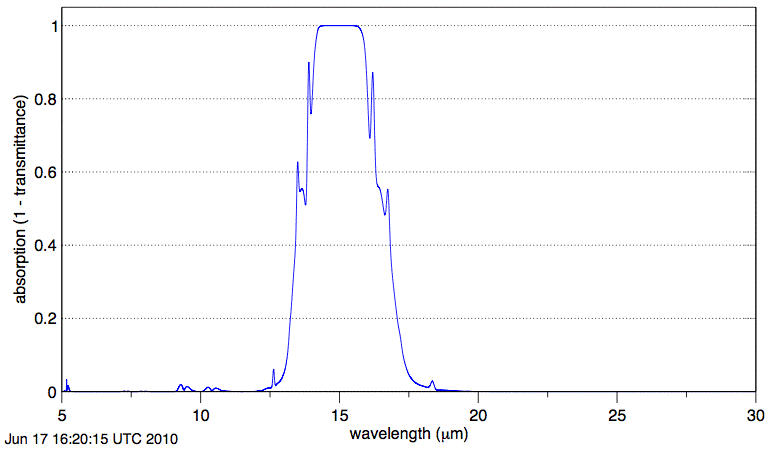
Absorption by CO2 along our 1-km path is negligible at wavelength 20 μm. The graph shows us that absorption of long-wave radiation by atmospheric CO2 is significant only in the range 12.5 μm to 17.5 μm.
In Water Vapor Continuum we found that a simple scaling of absorption with concentration is grossly inaccurate for water vapor. In Earth Radiator we showed that a 1-mm layer of water absorbs over 99.9% of all long-wave radiation. The graphs we present in Continuum Absorption Length imply that the same amount of water dispersed in a 1-km column of air will absorb less than 10% of long-wave radiation.
It turns out that a simple scaling calculation does not apply to CO2 either. If the absorption length of 20-μm radiation were 3 km in air with 330 ppm CO2, the Earth's atmosphere would be opaque to 20-μm radiation. But according to this popular graph, the CO2 in the Earth's atmosphere is transparent to 20 μm radiation.
In Absorption Line Broadening in the Infrared by Burch et al, we see how the presence of nearby molecules of all gases broadens the sharp absorption lines of the CO2 molecule. With high enough pressure, these lines become so broad that they overlap, and we see absorption of long-wave radiation at all frequencies within certain ranges, such as 13 μm to 17 μm.
We concluded that calculating the absorption spectra of water vapor and CO2 was far too big a project for us to embark upon. So we paid for a month's subscription to the most excellent Spectral Calculator. We asked the calculator to plot absorption by dry air with 330 ppm CO2 at 300 K and 1 atmosphere over a path length of 1 km. The calculator produced the following graph. For a logarithmic plot of the same data see here.

Absorption by CO2 along our 1-km path is negligible at wavelength 20 μm. The graph shows us that absorption of long-wave radiation by atmospheric CO2 is significant only in the range 12.5 μm to 17.5 μm.
Friday, June 11, 2010
Legal Examination
I'm looking at Research Paper No. 10-08 by Jason Johnston of the Institute for Law and Economics at the University of Pennsylvania (not to be confused with Pennsylvania State University where Michael Mann has his office). The idea of the report is to mimic a courtroom cross-examination of expert witnesses by non-scientist lawyers on the tenets of anthropogenic global warming. At first, we hoped that the report was a transcript of actual cross-examinations, but instead the cross-examination is performed by extracting quotations from peer-reviewed papers from climatology journals, and using these as answers to the questions posed by the author.
Here's one conclusion the author comes to. "Many of the ongoing disputes in climate science boil down to disputes over the relative validity and reliability of different observational datasets, suggesting that the very new field of climate science does not yet have standardized observational datasets that would allow for definitive testing of theories and models against observations."
In the section called "Questions about the Measurement of Land Surface Temperature Trends" the author discusses the global surface temperature provided by CRU, which we have examined in detail ourselves. But we never picked up on this point, which is the first one the lawyer-author makes.
"A daily average is computed as the midpoint between the nighttime minimum and daytime maximum temperature. From the mid 1950’s to the mid 1990’s, nighttime minimum daily surface temperatures in this dataset have risen about twice as fast as
daytime maximum daily surface temperatures.26 What is important to see is that most of the increase in global daily average surface temperature that is reported by the IPCC is due to an increase in nighttime minimum temperatures27 -- that is, daytime maximums have not increased by much over the period reported on by the IPCC."
The author assembles an explanation for why the nighttime minimums have risen, using quotations from existing papers. Every other sentence has a reference to a paper. According to the peer-reviewed literature, pavement replacing trees is one thing that raises nighttime minimums.
"There seems to be more and more evidence that there has indeed been a systematic trend upward since 1950 in the kind of variables that would have caused nighttime minimum temperatures to overstate actual surface warming."
This report will be a valuable resource to any lawyer challenging, for example, the EPA's ruling that CO2 is a pollutant. We ourselves have great faith in the courts as places where pseudo-science can be debunked. So we look forward to seeing lawyers taking on the climatologists.
Here's one conclusion the author comes to. "Many of the ongoing disputes in climate science boil down to disputes over the relative validity and reliability of different observational datasets, suggesting that the very new field of climate science does not yet have standardized observational datasets that would allow for definitive testing of theories and models against observations."
In the section called "Questions about the Measurement of Land Surface Temperature Trends" the author discusses the global surface temperature provided by CRU, which we have examined in detail ourselves. But we never picked up on this point, which is the first one the lawyer-author makes.
"A daily average is computed as the midpoint between the nighttime minimum and daytime maximum temperature. From the mid 1950’s to the mid 1990’s, nighttime minimum daily surface temperatures in this dataset have risen about twice as fast as
daytime maximum daily surface temperatures.26 What is important to see is that most of the increase in global daily average surface temperature that is reported by the IPCC is due to an increase in nighttime minimum temperatures27 -- that is, daytime maximums have not increased by much over the period reported on by the IPCC."
The author assembles an explanation for why the nighttime minimums have risen, using quotations from existing papers. Every other sentence has a reference to a paper. According to the peer-reviewed literature, pavement replacing trees is one thing that raises nighttime minimums.
"There seems to be more and more evidence that there has indeed been a systematic trend upward since 1950 in the kind of variables that would have caused nighttime minimum temperatures to overstate actual surface warming."
This report will be a valuable resource to any lawyer challenging, for example, the EPA's ruling that CO2 is a pollutant. We ourselves have great faith in the courts as places where pseudo-science can be debunked. So we look forward to seeing lawyers taking on the climatologists.
Monday, June 7, 2010
Hertzberg, Schreuder, and Siddons
Our correspondent Peter Newnam points us to a new paper that's being talked about on the Internet, Greenhouse Effect on the Moon?, by Hertzberg et al. The gist of the paper is that no planet acts like an ideal black body, therefore any calculation that is based upon the assumption that a planet is a black body is unreliable.
We use ideal objects like black bodies, the frictionless planes, and thin lenses all the time in physics and engineering. We use these ideal objects to estimate the behavior of the real world, and as we do so, we try to keep track of the error we are likely to make as a result of our ideal assumptions. Our hope is that the error is small compared to the accuracy we require of our calculation.
When Hertzberg et al. say that planets are not ideal black bodies, they are of course correct. But in the case of the moon, we see that the black-body model they present is pretty good. The actual temperature change on the moon is 80 K to 370 K, while the black-body model they present predicts a change of 35 K to 385 K. But Hertzberg et al. point out that the average temperature of the moon is roughly 40 K higher than predicted by a black-body model, and they claim that this difference invalidates the black-body analysis of planetary temperatures.
If we want a better understanding of the moon's surface temperature, we must add the heat capacity and conductivity of the surface rocks, as well as the absorption spectrum of these rocks for short-wave and long-wave radiation. Hertzberg et al. present a graph of the moon's surface temperature versus time during the day-night cycle. We see that the surface reaches its hottest temperature after the sun has passed the zenith, which indicates that the surface rock is taking time to heat up, by virtue of its heat capacity. The surface does not have a chance to reach its equilibrium temperature in the presence of the strongest sunlight. So we are not surprised that the moon fails to reach its black-body equilibrium temperature during the day. During the night, we see the temperature is still dropping at night when the sun rises again.
The albedo of the moon for short-wave radiation is around 0.1. It absorbs 90% of incident short-wave radiation from the sun. The emissivity of the moon's surface for long-wave radiation appears to be around 0.9. It emits 90% of the radiation that a black body would radiate. If the incident radiation from the sun is a uniform 350 W/m2, we expect the moon's surface temperature to be around 280 K. But the incident heat is not uniform. The moon spends half its time very cold, at around 80 K, in which state it radiates only 0.6% of the heat it would radiate at 280 K. For less than a third of the time, the temperature is above 300 K, reaching a maximum of 370 K. At 370 K, it radiates only 300% of the heat it would radiate at 280 K. We see that the excess of heat radiated during the day cannot compensate for the deficiency of heat radiated in the cool of the night. The moon does not radiate its own heat as efficiently as it absorbs the sun's heat, and so it is warmer than a constant-temperature black-body calculation predicts.
Hertzberg et al. conclude, "The ability of common substances to store heat makes a mockery of blackbody estimates." Quite the opposite is the case. If the moon conducted and stored heat well, its surface temperature would vary less, and the black-body estimate would be more accurate.
We use ideal objects like black bodies, the frictionless planes, and thin lenses all the time in physics and engineering. We use these ideal objects to estimate the behavior of the real world, and as we do so, we try to keep track of the error we are likely to make as a result of our ideal assumptions. Our hope is that the error is small compared to the accuracy we require of our calculation.
When Hertzberg et al. say that planets are not ideal black bodies, they are of course correct. But in the case of the moon, we see that the black-body model they present is pretty good. The actual temperature change on the moon is 80 K to 370 K, while the black-body model they present predicts a change of 35 K to 385 K. But Hertzberg et al. point out that the average temperature of the moon is roughly 40 K higher than predicted by a black-body model, and they claim that this difference invalidates the black-body analysis of planetary temperatures.
If we want a better understanding of the moon's surface temperature, we must add the heat capacity and conductivity of the surface rocks, as well as the absorption spectrum of these rocks for short-wave and long-wave radiation. Hertzberg et al. present a graph of the moon's surface temperature versus time during the day-night cycle. We see that the surface reaches its hottest temperature after the sun has passed the zenith, which indicates that the surface rock is taking time to heat up, by virtue of its heat capacity. The surface does not have a chance to reach its equilibrium temperature in the presence of the strongest sunlight. So we are not surprised that the moon fails to reach its black-body equilibrium temperature during the day. During the night, we see the temperature is still dropping at night when the sun rises again.
The albedo of the moon for short-wave radiation is around 0.1. It absorbs 90% of incident short-wave radiation from the sun. The emissivity of the moon's surface for long-wave radiation appears to be around 0.9. It emits 90% of the radiation that a black body would radiate. If the incident radiation from the sun is a uniform 350 W/m2, we expect the moon's surface temperature to be around 280 K. But the incident heat is not uniform. The moon spends half its time very cold, at around 80 K, in which state it radiates only 0.6% of the heat it would radiate at 280 K. For less than a third of the time, the temperature is above 300 K, reaching a maximum of 370 K. At 370 K, it radiates only 300% of the heat it would radiate at 280 K. We see that the excess of heat radiated during the day cannot compensate for the deficiency of heat radiated in the cool of the night. The moon does not radiate its own heat as efficiently as it absorbs the sun's heat, and so it is warmer than a constant-temperature black-body calculation predicts.
Hertzberg et al. conclude, "The ability of common substances to store heat makes a mockery of blackbody estimates." Quite the opposite is the case. If the moon conducted and stored heat well, its surface temperature would vary less, and the black-body estimate would be more accurate.
Wednesday, June 2, 2010
Continuum Absorption Length
Our job today is to convert this graph of water vapor continuum absorption coefficient versus frequency into a graph of absorption length versus wavelength. The original graph does not give absorption coefficient directly. Instead, it gives the absorption coefficient (in inverse centimeters) divided by the density of the water vapor (in molecules per cubic centimeter) divided by the water vapor partial pressure (in atmospheres). There are twelve plots in the graph, each representing the continuum absorption at a different temperature. We zoomed in on the graph and used a cross-hair cursor to translate several of the curves into numbers. You will find our numbers in the Water Vapor page of our Climate Spreadsheet here. We plotted absorption length for three combinations of water vapor concentration (in percent of volume), vapor pressure (in millibar), and temperature (in Kelvin). We superimposed the radiation spectrum of a black body at 300 K so that we can estimate the fraction of radiated power that will be absorbed by the first few kilometers of the Earth's atmosphere.
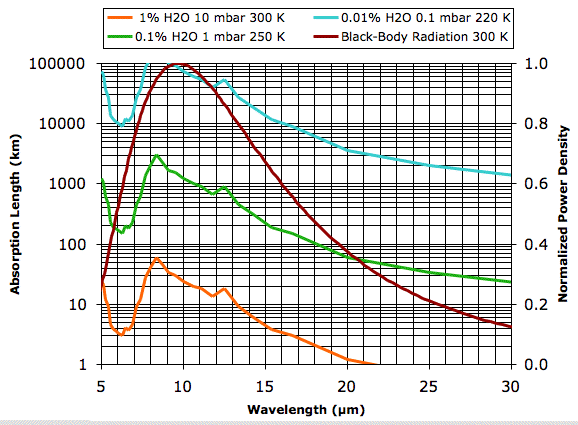
Plots of water vapor concentration versus altitude, such as this one for the Earth's atmosphere, show the concentration varying from as much as 4 % at sea-level to less than 0.0001 % at 10 km. Our plot of 1% water vapor at 10 mbar and 300 K is typical of the first 1 km of the atmosphere for 20° to 40° latitude on Earth. The absorption length of the water vapor continuum under these conditions is greater than 3 km for all wavelengths less than 16 μm. But for wavelengths greater than 20 μm the absorption length drops below 1 km. Looking at the graph, we estimate that 90% of the heat radiated straight up by the Earth's surface in these latitudes at wavelengths greater than 16 μm will be absorbed by water vapor before it reaches outer space.
Heat is radiated in all directions, which means most of it must pass through the atmosphere obliquely. Meanwhile, the atmosphere at the poles is dry, while the atmosphere in the tropics is humid. But the tropics are hotter than the poles, so that they radiate twice as much heat per square meter, and they cover a larger area too, so they contribute more to the total heat radiated by the Earth's surface.
Our guess is that almost all the heat radiated by the Earth's surface at wavelengths greater than 16 μm is absorbed by water vapor before it can reach outer space. These wavelengths represent roughly 30% of the total heat radiated by the Earth's surface.
PS. We spent several hours comparing our graphs with other calculations and measurements of water vapor absorption we found on the Internet. We believe we found good agreement between these calculations and measurements, although this agreement was not always obvious. For example, this graph from this report plots the absorption coefficient in cm2molecule−1, without mentioning the partial pressure. But we believe the graph corresponds to a partial pressure of 1 mbar. At 10.6 μm, the graph says 1.8 ×10−25 cm2molecule−1, while Cormier et al measured 1.82 ×10−22 cm2molecule−1atm−1 at the same wavelength. One atmosphere is almost exactly a thousand millibar.
PPS. So far as we can tell from sites like this one, absorption of long-wave radiation by the water vapor continuum is absorption by bonds between water vapor molecules, but does not include absorption by the bonds within the water molecules. Absorption within water molecules takes place at specific frequencies, so that a plot of absorption length versus wavelength contains valleys so sharp they appear only as lines. The line at 1.1 μm, for example, is only 0.00002 μm wide (see Figure 3 here). With one such line every 0.02 μm, the lines would absorb only 0.1% of the radiation emitted by a planet surface. But such lines have a tendency to get broader when the water vapor molecules are colliding with other gas molecules, and this broadening greatly increases the fraction of long-wave radiation these lines absorb. Thus, absorption by the water vapor continuum represents some, but not all, of the absorption by water vapor.
PPPS. This history of infra-red astronomy shows that we have to get up above 3 km in a dry part of the world in order to see infra-red light from outer space. Even then, we can see only wavelengths that neither water vapor nor CO2 will absorb, and the seeing is good only when we are looking straight up. See our Vapor Versus Liquid post and its ensuing comments for more details.

Plots of water vapor concentration versus altitude, such as this one for the Earth's atmosphere, show the concentration varying from as much as 4 % at sea-level to less than 0.0001 % at 10 km. Our plot of 1% water vapor at 10 mbar and 300 K is typical of the first 1 km of the atmosphere for 20° to 40° latitude on Earth. The absorption length of the water vapor continuum under these conditions is greater than 3 km for all wavelengths less than 16 μm. But for wavelengths greater than 20 μm the absorption length drops below 1 km. Looking at the graph, we estimate that 90% of the heat radiated straight up by the Earth's surface in these latitudes at wavelengths greater than 16 μm will be absorbed by water vapor before it reaches outer space.
Heat is radiated in all directions, which means most of it must pass through the atmosphere obliquely. Meanwhile, the atmosphere at the poles is dry, while the atmosphere in the tropics is humid. But the tropics are hotter than the poles, so that they radiate twice as much heat per square meter, and they cover a larger area too, so they contribute more to the total heat radiated by the Earth's surface.
Our guess is that almost all the heat radiated by the Earth's surface at wavelengths greater than 16 μm is absorbed by water vapor before it can reach outer space. These wavelengths represent roughly 30% of the total heat radiated by the Earth's surface.
PS. We spent several hours comparing our graphs with other calculations and measurements of water vapor absorption we found on the Internet. We believe we found good agreement between these calculations and measurements, although this agreement was not always obvious. For example, this graph from this report plots the absorption coefficient in cm2molecule−1, without mentioning the partial pressure. But we believe the graph corresponds to a partial pressure of 1 mbar. At 10.6 μm, the graph says 1.8 ×10−25 cm2molecule−1, while Cormier et al measured 1.82 ×10−22 cm2molecule−1atm−1 at the same wavelength. One atmosphere is almost exactly a thousand millibar.
PPS. So far as we can tell from sites like this one, absorption of long-wave radiation by the water vapor continuum is absorption by bonds between water vapor molecules, but does not include absorption by the bonds within the water molecules. Absorption within water molecules takes place at specific frequencies, so that a plot of absorption length versus wavelength contains valleys so sharp they appear only as lines. The line at 1.1 μm, for example, is only 0.00002 μm wide (see Figure 3 here). With one such line every 0.02 μm, the lines would absorb only 0.1% of the radiation emitted by a planet surface. But such lines have a tendency to get broader when the water vapor molecules are colliding with other gas molecules, and this broadening greatly increases the fraction of long-wave radiation these lines absorb. Thus, absorption by the water vapor continuum represents some, but not all, of the absorption by water vapor.
PPPS. This history of infra-red astronomy shows that we have to get up above 3 km in a dry part of the world in order to see infra-red light from outer space. Even then, we can see only wavelengths that neither water vapor nor CO2 will absorb, and the seeing is good only when we are looking straight up. See our Vapor Versus Liquid post and its ensuing comments for more details.
Subscribe to:
Posts (Atom)
