Falling Droplets

In Clouds Without Rain we saw immortal clouds circulating above a frozen planet, reflecting the Sun's heat back into space. We concluded that it is rain that saves our planet from freezing. It is rain that clears the skies so that the Sun's heat can reach us.

We must implement rain in our simulation, so that water vapor has some way of returning to the surface. Let us begin by considering how fast water drops fall through air. A falling drop accelerates until air resistance matches its weight. At that point, it continues to fall but it does not accelerate. It has reached its terminal velocity. In The Terminal Velocity of Fall for Water Droplets in Stagnant Air, Gunn et al. describe their apparatus for measuring the terminal velocity of water droplets, and present their measurements in graphs and tables. (The paper, published in 1948, is an enjoyable read that you can download here.)

We can calculate the terminal velocity of rigid, spherical objects using Stokes Law. Gunn et al. show that Stokes' Law applies well to water droplets of diameter less than 100 μm (one tenth of a millimeter). You may recall that the droplets in our simulated clouds are roughly 10 μm in diameter (one hundredth of a millimeter). For the droplets are small enough, surface tension is able to maintain a spherical shape in the face of air resistance.

But for droplets larger than 100 μm, Stokes Law over-estimates the terminal velocity. Larger droplets assume flattened shapes as they fall, and they are in constant motion, so that the air resistance they encounter is far greater than it would be for a rigid sphere. When the diameter exceeds 5 mm, the motion of the drop becomes so vigorous that the drop breaks into smaller drops.

The following graph shows the Gunn et al. measurements of terminal velocity, plotted against droplet diameter. We see that the maximum terminal velocity for the largest possible water droplets is around 10 m/s. For diameters less than 0.1 mm, Gunn et al. assure us we can use the terminal velocity given by Stoke's Law, so we also plot the terminal velocity calculated from Stokes' Law.



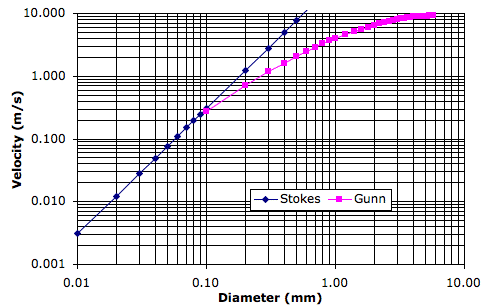
The 10-μm droplets in our simulated clouds will fall at a mere 3 mm/s through our gas cells. Given that our cells are a few hundred meters high, it will take a day or two for a cloud to fall from one cell to the cell below. Slow as this may be, the sinking of clouds does provide a way for water to move from one cell to another, and ultimately to return to the planet surface. In our next post, we will see how sinking clouds affect the result of our Cold Start simulation.