Anthropogenic Global Warming

The Anthropogenic Global Warming (AGW) hypothesis states that doubling the CO2 concentration of the Earth's atmosphere will raise the average surface temperature of the Earth by a minimum of 1.5°C, and more likely 3°C.

In our investigation of the absorption and emission of long-wave radiation by the Earth's atmosphere, we calculated that a sudden doubling of CO2 concentration would decrease the power the Earth radiates into space by 6.6 W/m². We then estimated how much the Earth and its atmosphere would have to warm up in order to restore the heat radiated into space to its original value. We assumed there would be no significant change in cloud cover as a result of the warming, and we applied Stefan's Law to calculate how the heat radiated by the Earth and its atmosphere would increase. We found that the required increase in surface temperature would be around 1.6°C. If there were no change in cloud cover, then the heat arriving from the Sun would remain the same, and we could expect the Earth to warm up by 1.6°C so as to once again arrive at thermal equilibrium.

The AGW hypothesis states that in the event of the Earth warming, changes in cloud cover will be such as to amplify the warming we calculate using Stefan's Law. Here is an extract from today's entry on Global Warming at Wikipedia.

The main positive feedback in the climate system is the water vapor feedback. The main negative feedback is radiative cooling through the Stefan–Boltzmann law, which increases as the fourth power of temperature.

As the Earth warms up, water evaporates more quickly from the oceans. Almost all water that evaporates must turn into clouds before it returns to Earth. Water condensing directly onto grass in the morning is an exception to this rule, but the vast majority of water vapor will return only as rain or snow, and so must first take the form of a cloud.

Clouds absorb long-wave radiation emitted by the Earth's surface, so the Earth cannot radiate its heat directly into space. Instead, the clouds radiate into space and warm the Earth with back radiation. Thus increasing cloud cover means less heat radiated into space for the same surface temperature. This is the positive feedback referred to by the AGW hypothesis. The AGW climate models predict that this positive feedback will amplify the minimum 1.5°C warming caused by CO2 to roughly 3°C. Some say 2°C and other say 4°C, but all agree that the actual warming will be greater than 1.5°C.

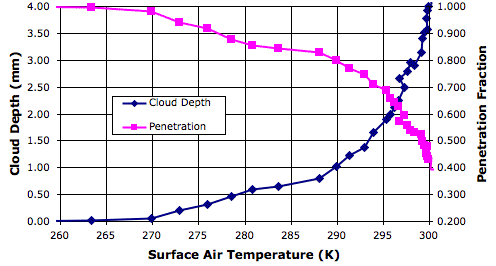
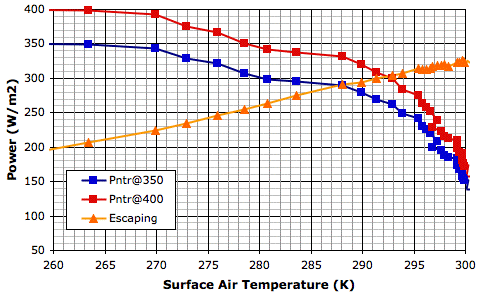
We see this positive feedback in our Circulating Cells simulation, version CC11, which simulates the formation of clouds as well as their absorption and emission of long-wave radiation. The graph below shows a close-up of the behavior of the simulation in the neighborhood of its equilibrium point for 350 W/m² solar power.



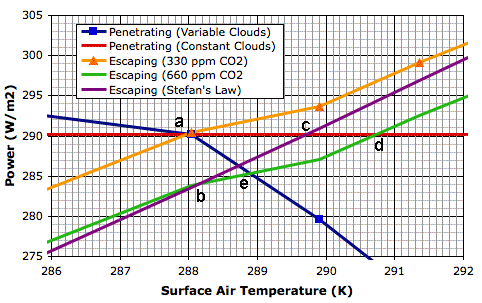
The blue line shows how the power that penetrates to the surface of our simulated planet varies with increasing surface temperature. The orange line shows how the total power escaping from our simulated planet increases with surface temperature. These two lines cross at a, where temperature is 288 K and total escaping power is 290 W/m². Our simulated atmosphere absorbs 50% of long-wave radiation, which is an adequate approximation of our atmosphere with its current concentration of CO2 (roughly 330 ppm).

The green line is the same as the orange line, but displaced down by 6.6 W/m², which is the amount by which we calculated the total power escaping from the Earth will decrease if we double CO2 concentration (to roughly 660 ppm). Thus the green line tells us the total escaping power at the same temperature if we were to double the CO2 concentration. Point b on the green line is 288 K, and the total escaping power is 283.4 W/m².



The purple line shows how the total escaping power will increase from b if we assume the cloud cover is constant and use only Stefan's Law to determine the heat radiated into space by the surface and atmosphere. The red line shows the solar power penetrating to the surface if we assume the cloud cover is constant. With constant cloud cover, the penetrating solar power does not change.

The purple and red lines meet at c, which is 289.6 K, or 1.6°C above the previous equilibrium point. Thus our simulation shows us that the warming due to CO2 doubling, if we ignore changes in cloud cover, will be 1.6°C, which is consistent with our previous calculation.

The green line, however, is the simulation's calculation of the total escaping power for increasing surface temperature. We see that the heat radiated into space does not increase as quickly as Stefan's Law would lead us to expect. And the reason for that is precisely the reason quoted by the AGW hypothesis: increasing cloud cover is slowing down the radiation of heat into space. The green line and the red line intersect at d, which is 290.7 K, or 2.7°C above our original equilibrium temperature. This is the new equilibrium temperature of the planet surface if we double CO2 concentration and we assume that there will be no change in the solar power penetrating to the surface while the cloud cover increases.



But the solar power penetrating to the surface must decrease as cloud cover increases. Clouds reflect sunlight. Thick clouds reflect 90% of solar power back into space. Even thin, high clouds reflect 10%. Increasing cloud cover will decrease the solar power penetrating to the surface. That is why our blue line slopes downwards. This is negative feedback, which acts against the positive feedback described by the AGW theory. The blue line shows how the solar power penetrating to the surface decreases as our cloud cover increases.

The blue line and the green line intersect at e, which is the equilibrium point we arrive at after doubling the CO2 concentration and considering both the positive feedback of back-radiation and the negative feedback of solar reflection. The temperature at e is 288.9 K, which is 0.9°C above our original equilibrium temperature.

Thus our simulation shows how the negative feedback generated by clouds dominates their positive feedback, and suggests that the actual warming of the Earth's surface due to a doubling of CO2 will be closer to 0.9°C than the 3°C predicted by the AGW hypothesis.

Equilibrium Point

Heat arrives at the Earth in the from of sunlight. The clouds reflect some of it. Almost all the rest arrives at the Earth's surface. Of the sunlight that reaches the surface, some is reflected back into space, especially by snow, but most is absorbed. To the first approximation, therefore, sunlight affects the climate only by it warming the surface, not by warming the atmosphere directly.

In our Circulating Cells simulation, version CC11, solar power is either reflected by clouds or absorbed by the surface. The only way for heat to enter the atmosphere is by contact with the surface, so it is the temperature of the surface that drives the the circulation of gases and the creation of clouds, snow, and rain. When we observe, for example, that 80% of solar power is penetrating to the surface when the surface gas temperature is 290 K, we can assume that the 80% of solar power will penetrate to the surface whenever the surface gas temperature is 290 K.

Our program of solar increase provides us with observations of cloud depth and penetrating power for a range of solar powers, and therefore for a range of surface temperatures. The following graph shows how the fraction of solar power penetrating to the surface varies with surface temperature.



In our simulation we calculate the penetrating power for each surface block using the depth of the clouds in the column of cells above the surface block. We cannot, however, use the average cloud depth to obtain a measurement of average penetration fraction. When we do so, our measurement is always too low, because there are gaps in the cloud cover, and these gaps allow more light to pass through than if the clouds were distributed uniformly.

In the following graph, we have taken our measurements of penetration fraction and used them to calculate the power that would penetrate to the surface for two values of solar power: 350 W/m² and 400 W/m². Along with these penetrating powers, we also plot the total escaping power.



At thermal equilibrium, the total escaping power must be equal to the penetrating power. Thus the intersection of the penetrating power and escaping power graphs occurs at the equilibrium temperature. For solar power 350 W/m², the intersection occurs at 288 K. For 400 W/m², the intersection occurs at 292 K. These are, of course, the same equilibrium temperatures we obtain from our existing graph of surface temperature versus solar power.

In our next post, we will use the above graph and the calculations we presented in With 660 PPM CO2 to estimate how much the Earth would warm up if we doubled the CO2 concentration of its atmosphere.

Conservation of Heat

In Solar Increase we were concerned that our program of increasing solar power did not allow adequate time at each value of solar power for the simulation to arrive at thermal equilibrium. As we described in our previous post, we now have measurements of the state of the simulation at each value of solar power. The following graph plots penetrating power, total escaping power, and downwelling power versus solar power. The penetrating power is the power per square meter that gets to the surface through the clouds. The total escaping power is the power per square meter that the surface and atmosphere together radiate into space. The downwelling power is the power arriving back at the surface from the radiating clouds.



The downwelling power is increasing because the cloud layer is getting thicker. The clouds radiating heat towards the surface are lower down and therefore warmer. But it is the equality of the penetrating and escaping power that interests us the most today. At thermal equilibrium, the total escaping power should be equal to the penetrating power. And indeed we see that this appears to be the case for all values of solar power.