Carbon-14: The Reservoir Is the Ocean

Up to now, we have guessed that the carbon-14 reservoir in our carbon cycle is the deep ocean, where the concentration of carbon-14 is 80% of the concentration in the atmosphere. We are using 1.0 ppt (parts per trillion) as the concentration in the atmosphere, and 0.8 ppt as the concentration in the deep ocean, but we recognize that the absolute concentration in the atmosphere is hard to measure, and might be slightly higher than 1.0 ppt. But the concentration in the deep oceans is well-known to be 80% of that in the atmosphere. Today we argue that the reservoir of carbon-14 in our carbon cycle must be the deep ocean.

Our calculations so far go like this. Every year, cosmic rays create 7.5 kg of carbon-14 from atmospheric nitrogen. Carbon-14 decays back into nitrogen with a half-life of 5700 years, which means 0.012% of it decays into nitrogen every year. After fifty thousand years, the total mass of carbon-14 in the atmosphere will reach equilibrium. The total mass of carbon-14 will be 62,500 kg, because 62,500 kg multiplied by 0.012% is 7.5 kg per year, so the rate at which carbon-14 is created by cosmic rays is equal to the rate at which the Earth's reservoir of carbon-14 decays back into nitrogen.

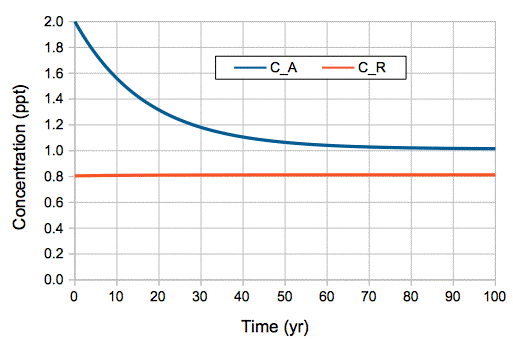
The natural, equilibrium atmosphere of the early twentieth century contained 650 kg of carbon-14. The remainder of the Earth's 62,500 kg of carbon-14 is elsewhere, in the reservoir of our carbon cycle. Almost all carbon-14 in the atmosphere exists in CO2. By whatever means a carbon-14 atom moves in and out of the atmosphere, it does so in CO2 molecules. When one carbon-14 molecule moves into the reservoir, it does so in the company of 1÷1.0 ppt = 1.0 trillion CO2 molecules. If the reservoir is the deep ocean, where the concentration of carbon-14 is 0.8 ppt, we can further say that, whenever a carbon-14 atom re-enters the atmosphere from the ocean, it does so in the company of 1÷0.8 ppt = 1.25 trillion CO2 molecules.

We calculated that the reservoir, assuming it is the deep ocean, must contain 77,000 Pg of carbon, and that every year 37 Pg of carbon must be exchanged between the reservoir and the atmosphere, all of it moving with CO2 molecules. When 37 Pg of carbon moves from the atmosphere to the reservoir, it carries with it 37.0 kg of carbon-14. When 37 Pg of carbon moves from the reservoir to the atmosphere, it carries with it 29.6 kg of carbon-14. The difference is a net 7.4 kg of carbon-14 flowing into the reservoir every year. We add to this another 0.1 kg per year, which is the decay of the carbon-14 that remains in the atmosphere, and we arrive at a total of 7.5 kg of carbon-14 being removed from the atmosphere by exchange and decay, which gives us equilibrium with the 7.5 kg per year being created by cosmic rays.

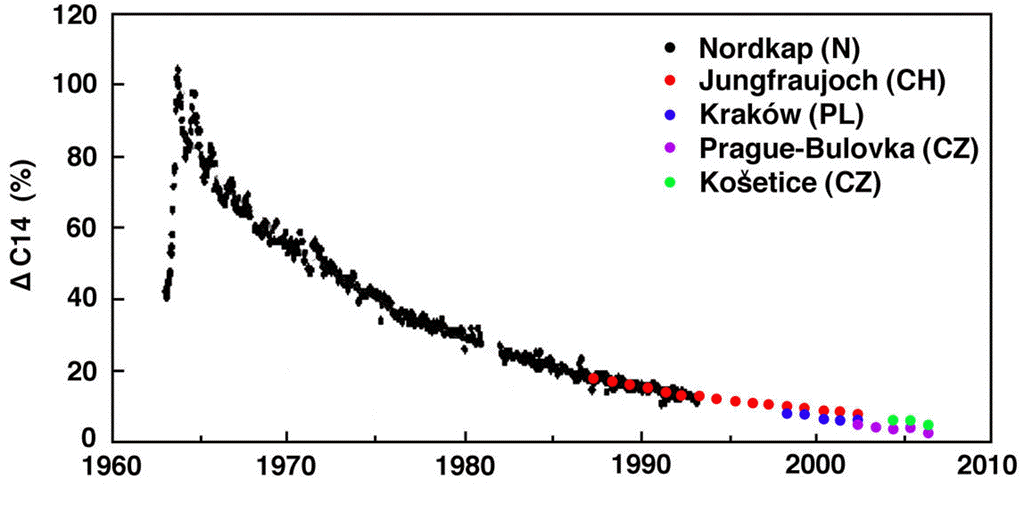
With the above values of reservoir size and annual mass exchange, we obtained an analytic solution to the carbon-14 concentration in our natural, equilibrium atmosphere. We showed that this analytic solution was in near-perfect agreement with the relaxation-time of atmospheric carbon-14 concentration following the nuclear bomb tests of the 1950s and 1960s. Thus we are confident that our analytic solution is a reliable model for predicting the behavior of carbon-14, and therefore of all carbon, in the Earth's atmosphere.

Let us consider the possibility that the reservoir of our carbon cycle resides somewhere other than the deep ocean. The table below shows other candidates for the reservoir, their carbon-14 concentrations, and the relaxation-time of carbon-14 concentration that we would obtain if this candidate were indeed the carbon-14 reservoir. We refer to Arnold et al. for our normalized concentration values, in which the atmospheric concentration is taken to be 1.0 ppt.

Candidate	Carbon-14 Concentration (ppt)	Relaxation Time (yr)
Ocean, Below 1000 m	0.80	17
Ocean, Top 100 m	0.96	3.5
Biosphere, Land	1.00	0.0
Biosphere, Ocean	0.96	3.5
Soil, Humus	1.00	0.0

The above candidate reservoirs are the only ones known to us that exchange CO2 with the atmosphere. The relaxation-time of carbon-14 concentration after the nuclear bomb tests was roughly 15 years. None of the above candidates are even close to being consistent with the aftermath of the bomb tests, except for the deep ocean, which is in excellent agreement. We conclude that the reservoir of our carbon cycle is the deep ocean and only the deep ocean. The other candidate reservoirs do exchange CO2 with the atmosphere, but whatever effect they have upon the Earth's carbon cycle is dwarfed by the flow of carbon into and out of the deep ocean.

Carbon-14: Absolute and Relative Concentration

Suppose we want to measure the carbon-14 concentration in a cubic meter of gas. If we can measure the rate at which the gas emits beta particles, we will know the number of carbon-14 decays occurring per second. Because 0.012% of carbon-14 atoms undergo beta decay every year, we can deduce the number of carbon-14 atoms in the gas from the decay rate. By some chemical procedure, we measure the amount of carbon in the gas, and so we can deduce the carbon-14 concentration.

To measure the rate at which the gas produces beta particles, we put the gas in a chamber. All around the chamber we arrange devices that detect beta particles. We will not be able to cover the entire surface area with beta detectors, but we can measure the fraction we cover. If we cover half the area, we can assume half the beta particles emerging from the gas will strike one of our detectors. The detectors may not detect every beta particle that strikes them. But we can perform experiments to measure their efficiency. We end up with a scaling factor by which we can multiply the number of beta particles we detect to obtain the number of beta particles that left the gas volume.

The beta particles have energy up to 156 keV, with a Fermi-Dirac distribution. The most energetic of them can penetrate 100 mm of air. But they are not certain to do so. The least energetic of them can penetrate only a few millimeters of gas. Only a small fraction of the beta particles emitted by carbon-14 decaying within our cubic meter of gas will ever make it to our detectors. But we can, with the help of the continuous slowing-down approximation, and the Fermi-Dirac distribution, estimate the fraction of beta particles that will emerge from the gas volume. And so we can obtain a scaling factor by which to multiply the number beta particles we detect to obtain the total number of beta particles emitted by the gas.

Having performed these calculations, we start to count beta particles. If the gas contains 300 ppmv of CO2 and 1.0 ppt of carbon-14, there will be of order 2.6×10¹¹ carbon-14 atoms in the gas. Of these, 3.1×10⁷ will decay each year, or 0.97 per second. Our chamber is 50% covered with detectors that are 50% efficient, and only 10% of our beta particles get out of the gas volume, so we expect to detect of order one beta decay every forty seconds.

Before we make our first measurement, we evacuate our chamber, to measure the background rate of beta particles. We find that our beta detectors are detecting one or two beta particles per second. These are due to radioactive isotopes in the chamber walls, cosmic ray showers, and electronic noise.

At this point, we realize that measuring carbon-14 in a gas is going to be hard. So we freeze the carbon dioxide out of our gas sample and put a pellet of solid CO2 into a much smaller chamber. We still have the same problems, but they are less severe. We can reduce our background beta-particle rate to one every ten seconds, while raising our carbon-14 beta rate to one per second. We will have to admit, however, that our measurement of carbon-14 concentration will be accurate to no better than ±20%. And indeed, the measurements of atmospheric carbon-14 concentration vary from 1.0 to 1.5 ppt.

But it is much easier to measure the relative concentration of carbon-14 in various samples of gas, water, or wood. We put one sample in our chamber and count beta particles, then another sample. If our first measurement is 20% too high, so will the second one, because the 20% error is a feature of the chamber, not the sample. The upshot of these practical considerations is that we can say that the deep oceans have carbon-14 concentration 80% of atmospheric, and be confident to ±2%, but we cannot say what the actual deep ocean concentration is to better than ±20%.

So far, we have assumed that the atmospheric concentration of carbon-14 is 1.0 ppt. In fact, it may be as high as 1.5 ppt. If it is 1.5 ppt, we have 980 kg of carbon-14 in our natural, equilibrium atmosphere, instead of the 650 kg we calculated assuming 1.0 ppt. This 980 kg is still negligible compared to the 62,500 kg of carbon-14 in the reservoir. And it is the relative concentration in the deep ocean that dictates the values of the mass exchange rate and reservoir size in our carbon cycle model, not the absolute concentration.

Thus, it may be that the atmosphere contains 1.5 ppt of carbon-14, not 1.0 ppt, but this has no significant effect upon our conclusions. We will continue to assume that our natural, equilibrium atmosphere contains 1.0 ppt, and quote concentrations in other potential reservoirs of carbon-14 as a fraction of the atmospheric concentration, just as the authors do in Arnold et a., where they use "relative specific activity corrected for fractionation".

Carbon-14: The Bomb Tests

Between the years 1945 and 1962, we detonated hundreds of atomic bombs in the atmosphere. Most of these, and certainly the largest, were detonated in the five years leading up to the Partial Test Ban Treaty in late 1963, which banned further atmospheric detonations. Atomic explosions produce carbon-14. By 1964, bomb tests had produced enough carbon-14 to double the atmospheric carbon-14 concentration. The graph below shows atmospheric carbon-14 concentration relative to its value before the bomb tests, as measured by various groups.


Figure: Atmospheric Concentration of Carbon-14 During and After the Bomb Tests. This graph is from an essay by Pettersson. The author combined measurements from several stations to produce the most complete graph we could find. For alternate plots, see here and here.
The relaxation of the atmospheric carbon-14 concentration from its peak follows an exponential decay with time constant roughly 15 years. After fifty years, the concentration is within a few percent of its value before the bomb tests. The carbon-14 did not linger in the atmosphere. It disappeared. Let's see if our model of the Earth's carbon cycle predicts this same relaxation or not.

In our model, carbon-14 concentrations are governed by two differential equations. We already solved these equations for a starting-point of zero in the atmosphere and the reservoir. Using the same procedure, we can solve the equations for a starting point of 2.0 ppt in the atmosphere and 0.8 ppt in the reservoir, which is the state the atmosphere was in at the time of the Partial Test Ban Treaty, when atmospheric tests were stopped. We obtain the following solutions for atmospheric concentration, C_A, and reservoir concentration C_R.

C_A = 1.0 + 0.987 e^−t/17 + 0.013 e^−t/8200
C_R = 0.8 + 0.0089 e^−t/17 − 0.0089 e^−t/8200

We note that this as t → ∞, we have C_A → 1.0 ppt and C_R → 0.8 ppt, as before. Whatever carbon-14 we add to the atmosphere, it will eventually decay, and we will be left once again with the concentrations generated by cosmic ray production. The above equations produce the graph of atmospheric and reservoir concentration shown below.


Figure: Carbon Cycle Model's Prediction of Atmospheric and Reservoir Carbon-14 Concentration After Sudden Doubling of Atmospheric Concentration.
Our simple, two-part, uniform-reservoir model of the carbon cycle predicts an exponential relaxation of carbon-14 concentration after the bomb tests, with a time constant of 17 years. Needless to say: agreement between the model and observation is superb.