Today's post is longer than usual. We present a mystery that we would like you to help us solve, but we also describe what happens to our simulation when we try to make sure that cell circulations take place quickly enough to be consistent with simulation time.
In Work by Circulation we showed that the rising cell does more work in the act of expanding than is required to compress the falling cell. This excess work will accelerate the cells so that they circulate. If the expanding cell cools by 3.032 K and the falling cell warms by only 3.000 K, the missing 0.032 K represents heat and pressure energy that has been converted into work. With heat capacity 1 kJ/kg, there will be 32 J of work available for each kilogram of gas in the rising cell. When divided between the four cells, there will be 8 J/kg. We call this the expansion work.
Convection occurs in water as well as air. Water at 20°C is 0.2% less dense than water at 4°C. A cell of water at 20°C will be buoyant within water at 4°C. We often think of water as an incompressible fluid. But it is slightly compressible. Water at 100 kPa is 0.004% less dense than water at 200 kPa. Water at 20°C rising from a depth of 10 m to the surface of a lake will do 6 mJ/kg of work by expansion. Meanwhile, water at 4°C falling from the surface to a depth 10 m will require 0.2% less work for its compression. The excess 12 μJ/kg is adequate to accelerate four equal cells to 2.5 mm/s. It is conceivable, therefore, that expansion work can power convection in water.
Nevertheless, there appears to be another source of work to power circulation. In a block of four cells, if we have a hot cell on the lower-left and a cold cell on the upper-right, the block's center of mass will descend when we rotate clockwise. The upper-left cell slides off the hot cell to rest upon the cold cell. As it slides, the top-left cell pushes the other three cells around to complete the circulation. The circulate routine of CC4 calculates how far the center of mass of a block of four cells will descend if we rotate the block by a quarter-turn. We describe this calculation in a comment here. If the block's center of mass drops by 0.8 m in gravity 10 N/kg, the weight of the block will provide 8 J/kg of work. We call this the buoyancy work.
In CC3 we rotated a block of cells only if the buoyancy work was positive. We ignored the effect of expansion work and buoyancy work upon the cells. Of the heat we put into the array at the bottom, only 85% emerged from the top by radiation. In CC4 we calculated the expansion work and divided it up between the four cells to represent viscous heating. At equilibrium, 100% of the heat we put in emerged from the top. Our simulation conserved heat, but it ignored buoyancy work. How can that be?
Furthermore, how large is the buoyancy work compared to the expansion work? If one is positive, is the other always positive? The circulate routine of CC5 includes code that calculates both the buoyancy work and expansion work, and reports them both. We ran our simulation with this code activated. In a wide variety of conditions, both evolving and convergent, the buoyancy work was always between 95.7% and 97.6% of the expansion work. To within the margin of error introduced by our simulation, buoyancy and expansion work are equal.
Why are they equal? Michele has proved to me several times that for adiabatic circulation, temperature will drop linearly with altitude. Could it be that this linear relationship causes buoyancy and expansion work to be equal? Or are buoyancy work and expansion work just two faces of the same process, so that we can count one or the other, but not both? If they are one and the same, then buoyancy work cannot exist without expansion work, which implies that convection would not occur in a perfect, incompressible fluid. But surely convection can occur in a perfect, incompressible fluid?
We would like to provide you with answers to these questions, but we don't have them yet. Perhaps, after a few more debates with Michele and anyone else who wants to take part, we will have answers. For now, however, we are going to assume that we cannot add buoyancy and expansion work together to obtain the total work available to accelerate our cells. We have a simulation that conserves heat at equilibrium, and we want to keep it that way. We will calculate and use the expansion work only, and add it back to the cells as viscous friction.
In the circulate routine of CC5, we calculate the drop in the combined temperature of the four cells in a block. We call this net loss our impetus for circulation. If the impetus is 0.032 K, our expansion work will be 8 J/kg when spread among the four cells. The cells could, in theory, reach a speed of 4.0 m/s. The cells in our atmospheric array are roughly 400 m high, so a circulation at 4 m/s will take place in 100 s. There are 450 cells in our 15×30 array, and our simulation picks a new block on every iteration. We expect one of the four cells in our block to be picked again within a hundred iterations. But one hundred iterations corresponds to 100 s, so we see 0.032 K is the minimum impetus required to make sure that our rotation takes place before we expect one of its cells to take part in another rotation.
Our CC5 program rotates a block of four cells only if its impetus for circulation is greater than an impetus threshold. With the impetus threshold set to 0.032 K, we ran CC5 to produce new versions of the graphs we presented in Simulation Time.
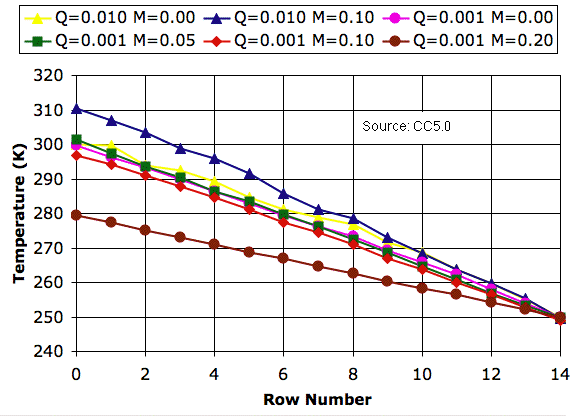
The impetus threshold has no effect upon the profiles we obtain with no mixing (M = 0.0). Nor do we see any effect with heavy mixing (M = 0.20). We do, however, see a slight change in the presence of mild mixing (M = 0.05). Mild mixing now raises the surface temperature by a few degrees.
The impetus threshold makes sure that rising cells are significantly warmer than falling cells. When a cell rises from row 7 to row 8, its temperature drops by a factor of 0.9879 (see here). If our impetus threshold is 0.03 K, warm cells about to rise from row 7 must be 0.03 K ÷ (1-0.9879) = 2.5 K warmer than cool cells about to arrive in the same row. Between the bottom rows, the required difference is 3.0 K, and between the top rows it is 1.7 K. With Q = 0.001 K, a cell freshly-arrived in the bottom row will warm by 3.0 K in three thousand iterations, which is almost an hour. Soon after, it will start to rise.
In our next post, we will see how well our program performs when we simulate night and day using CC5's new Rotating Greenhouse configuration.
PS. You will find the equilibrium array for Q = 0.001 K and M = 0.00 in PGH_Q001_M00. The array for Q = 0.001 K and M = 0.20 is PGH_Q001_M02. Saved arrays now have comments in them that tell us the conditions under which they were obtained.

No comments:
Post a Comment