We are well aware that air taking part in atmospheric convection will cool down as it rises, and warm up as it falls, but this circulation is powered by heat absorbed from the planet and subsequently radiated into space by the atmosphere. It is not spontaneous or self-generated. The circulation requires that the planet surface be warmed by the sun and that the atmosphere be capable of radiating heat into space at higher altitudes. With no heat flow, there will be no circulation, and no temperature difference between top and the bottom of the atmosphere. In other words: there is no such thing as adiabatic magic, as we will now demonstrate.
The diagram below shows how we can use adiabatic magic to create a machine that is 100% efficient at turning heat into work. Such a machine is also known as a perpetual motion machine of the second kind.
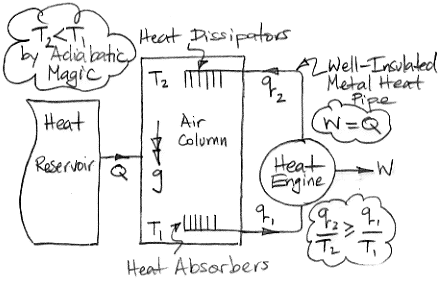
In the center of the diagram is an air column. The action of gravity is indicated by the double-headed arrow with the letter g. The column is high enough that the weight of the air it contains causes the pressure to be greater at the bottom than the top. By adiabatic magic, the bottom of the column is hotter than the top, so T1 > T2. We exploit this temperature difference with a heat engine. Metal veins absorb heat from the air at base of the column. A metal rod, well-clad with thermal insulation, carries this heat to a heat engine. A heat engine is something like a steam turbine, which exploits the flow of heat from hot to cold in order to generate work. Heat flows out of the engine through another metal rod to top of the column. The heat flowing into the engine is q1 and the heat flowing out is q2. The work produced by the heat engine is W. We express the heat flow and work output in Watts.
The First Law of Thermodynamics requires that W = q1 − q2. The Second Law of Thermodynamics requires that the entropy of the heat going in must be less than or equal to the entropy of the heat going out. With the absolute temperature scale, this means that q1 / T1 ≤ q2 / T2. Subject to these constraints, we see that our heat engine can produce work by exploiting the temperature difference between the bottom and the top of the air column.
Of course, we are taking more heat out of the bottom of the column than we are restoring to the top, so the total heat of the column will tend to decrease. We're not sure what the adiabatic magic theory has to say about an air column as it cools, so we are going to avoid this issue by adding heat to the column from a large reservoir. We add exactly as much heat as the column is losing by the action of the heat engine. The heat we add is Q, so Q = q1 − q2 = W.
So now let us consider the air column and the heat engine acting together. They constitute a perpetual motion machine. We see that we have Q entering the machine and W leaving. The machine turns heat into work with 100% efficiency. It is a perpetual motion machine of the second kind.
The adiabatic magic idea is one of a class of impossible ideas: those that propose the spontaneous separation of heat into hot and cold. The above diagram could be adapted to disprove any such idea with equal facility. If someone claimed they had invented a new material that always became hotter at one end than the other, even with no heat flow from one end to the other, we could disprove his claim with the above diagram.
Because adiabatic magic is impossible, we see that a transparent atmosphere can be no warmer at the bottom than at the top. Transparent gas cannot radiate heat into space (see Radiative Symmetry). In the case of Venus, if nothing heats the surface, the gas at the surface will be no warmer than the gas at the altitude to which sunlight does penetrate.
Of course, our atmosphere does radiate heat into space, so the lower air is warmer than the upper air, in order to transport that heat. And Venus's atmosphere gets hotter all the way to the surface, which means it is transporting heat away from the surface and radiating it into space.

Thank you for explaining to me why I've been rather troubled by the adiabatic process whereby the bottom of an atmosphere is supposed to be hotter than the top. In my simpleminded way of thinking about these things, this seems to suggest that heat is somehow generated ex nihilo.
ReplyDeleteI very much like the idea of the perpetual motion machine. It shows very clearly why it's nonsensical. Would it be going too far with it to imagine that in a sufficiently dense or deep atmosphere, the bottom layers would be so hot as to turn into high-pressure steam, which could be used to drive a steam turbine in perpetuity?
Adiabatic magic is a great name for it.
On second thoughts, there would seem to be another explanation why this perpetual motion machine wouldn't work. It goes like this:
ReplyDeleteEven if we suppose that in the air column T2 at the top is less than T1 at the bottom, with some sort of more or less linear variation in temperature between the two, the same would apply to the well-insulated "external" pipe and heat engine. The result would be that the actual temperature difference across the (presumably small) heat engine itself would be much less than the temperature difference between T1 and T2, and would be almost (entirely?) useless for the purpose of performing useful work.
Dear Frank,
ReplyDeleteI'm very glad you enjoyed the entry and the choice of title. Let me try to answer your objection to my well-insulated pipe. Let the pipe be made of solid copper about a hundred meters in diameter, so that it's cross-sectional area is ten thousand square meters. Let the column of air be ten kilometers tall, so our pipe is ten kilometers long, leading up from T1 at the base of the air column to T2 at the top, and at the top we place the heat engine.
Copper has conductivity 390 W/mK, so our pipe will convey 390 W along its 10,000 m length with a 1°C temperature drop, because it's area is 10,000 square meters. Now let us surround the copper pipe with another pipe and evacuate the air from between the two pipes. The vacuum conducts no heat.
If it were a black body, the copper pipe surface would radiate 460 W/m2. But we polish it so it's shiny, and it emits only 50 W/m2. We put a 99% reflecting mirror finish on the inside of the vacuum pipe, so it absorbs only 500 mW/m2. We give this vacuum pipe an outer mirror finish and surround it with yet another vacuum pipe with an interior metal finish. We get 5 mW/m2 radiated from the first pipe and only 50 μW/m2 absorbed by the second. We put a mirror finish on the outer surface of the second pipe and surround it with a third vacuum pipe, whose inner surface is also a mirror finish. The third pipe absorbs only 5 nW/m2.
The total surface area of the copper pipe is roughly 4,000,000 m2, so the total heat lost through the three vacuum insulators is only 20 mW = 0.02 W, which is much less than the 390 W the pipe is carrying.
We see that we have 300 K at the bottom of the pipe, 299 K at the top, and the air at the top is at around 220 K. We have 79 K temperature difference available for the heat engine.
Expensive, but possible, so the perpetual motion machine is possible, so Adiabatic Magic remains impossible.
Aaah...
ReplyDeleteFor some reason or other, I'd been thinking that these were hollow pipes filled with air. For me, a "pipe" is something that's hollow. Replace them with solid cylinders of copper - near-perfect conductors - and my objection melts away.
But then it comes back to this adiabatic lapse rate thing. In trying to get my head round it, I've supposed that it's something that grows out of the gas law P.V = k.T. Increase the pressure, and you increase the temperature. And at the base of the atmosphere, the pressure must be higher.
I'm interested in all this because, as a somewhat naive student of physics, I've been trying to construct a simple climate simulation model from first principles. I started out by thinking of one square metre of the surface of the rotating Earth (without any atmosphere) being warmed by the Sun, and the heat being conducted into the ground, and also being re-radiated into space (Stefan-Boltzmann law). That was quite easy to do. So then I thought I'd pour an atmosphere on top of the square metre, which would absorb and re-radiate some fraction of this radiation going through it. That's when I came across this adiabatic lapse rate business. And a variety of other problems (e.g. convection, clouds, wind). It's got me pretty comprehensively foxed.
But I don't give up easy! I'm not through trying yet! ;-)
Dear Frank,
ReplyDeleteYou are quite right, of course: a pipe is something hollow. I should have said rod. So I will correct the blog post. Apologies for the lack of clarity, and for thinking that you could not make the insulated rod argument for yourself.
I commend you for your ambition to build your own climate model. You will find that obtaining the absorption spectra of the atmospheric gasses is hard. I don't want to be immodest, but I think I have done a decent job building up a climate model so far, starting with Extreme Greenhouse last February, and culminating in a computer program you can run yourself that calculates total power radiated into space under different conditions.
As to adiabatic lapse rate, yes it comes out of the gas law plus the ratio of the gas's specific heat at constant pressure to specific heat at constant volume. For a diatomic gas like N2 and O2 this ratio is 1.4. You do work on the gas when you compress it, and if you assume no heat gets out, you get the adiabatic relationship between pressure and temperature. I show how the equation works in Atmospheric Convection.
Yours, Kevan
Thanks. I'll take a look at those pages. But I'm sure you'll understand that I like to write the simulation models myself, because that way I know what assumptions have gone into them.
ReplyDeleteIs there an index of related pages anywhere?
Frank
The blog page allows you to select posts on Climate Models, which I think should bring them out for you. Another way of doing it would be to start with the post where I first present the Total Escaping Power model. I think you'll find the code is so simple with enough comments for you to be able to see exactly what is going on. I have the data available too. It would be a pity if you started from scratch to obtain the spectra when I have done the work and payed the subscription fee to the Spectral Calculator.
ReplyDeleteHi Kevan
ReplyDeleteInteresting blog.
I had been trying to get a handle on the adiabatic atmosphere and found your site
Just been reading some of your posts and they are very thought provoking.
I have a few niggles however.
All the derivations of the dry adiabatic lapse rate that I have come across analyse it from the static balance of gravitational force and pressure difference on a parcel of air.
No convection term is involved.
Apparently this situation is relatively stable and the meteorologists call this the neutral position.
Of course Newtons first law for balanced forces includes uniform velocity as well as the rest position.
So for a parcel of dry air given an initial gentle vertical push it appears that it will move vertically up for quite a few kilometres without any further external force.
The potential energy gain of the parcel is matched by a potential energy loss of the air falling down to fill the void left by the ascending parcel.
At the tropopause cooling of the parcil takes place.
As well as up convection we have down convection.
I have a mental image of the Cartesian diver and the Atwood Machine as near analogues of the adiabatic atmosphere.
Perhaps I am missing something?
Bryan
Dear Bryan,
ReplyDeleteWelcome to the site. Thank you for your compliments. I don't think you are missing something so much as you have accepted the belief of contemporary climate scientists that the adiabatic lapse rate is the natural state of an atmosphere. That's not true. The adiabatic lapse rate is the temperature gradient that builds up in an atmosphere when it must transport heat from the planet surface to the tropopause.
When we heat the atmosphere from below, the temperature gradient grows until it reaches −0.01 K/m (that's g/Cp). After that, the gradient can't grow any more because air moves freely up to the tropopause by convection, where it radiates heat into space, and then descends. At this point, your cartesian diver analogy applies to the circulating cells of air.
This Adiabatic Magic post shows that it takes work to develop the adiabatic lapse rate in the atmosphere.
Once the lapse rate is set up, it also requires work to maintain, because heat is always flowing by conduction and radiation from the hot air to the cold air.
When you say "upward" and "downward" convection, I don't know what you mean. Convection is a circulation of gas, so there is always some upward and some downward.
We look into how fast the lapse rate builds up and collapses in our series of posts on Circulating Cells, with the help of a simulation program. We describe the forces that motivate convection in Impetus Dissected. We derive the adiabatic lapse rate on the basis of assumptions that we believe are clear and simple in Temperature Pressure and Altitude.
I hope you will find these further posts interesting. We set off on our investigations because we were unable to find satisfactory answers in the atmospheric literature. But we have found answers of our own that have stood up to examination from all angles, and have enjoyed ourselves. I like to think that I (and my very few readers) are open to correction, and would welcome your further comments.
Yours, Kevan