Simulated Rain

The latest version of our Circulating Cells program implements the simplified evaporation cycle we presented in our previous post. Freezing clouds turn into snowflakes and drift downwards. When the snowflakes pass through warm air, they melt and become raindrops. To run the program, download CC10 and follow the instructions at the top of the code.

We run the simulation starting with our cold-start state, CS_0hr. The program runs ten times slower than before. The water balancing calculations are more complex now that we have added precipitation, and we must perform them more often because rain and snow move quickly through the atmosphere. Nevertheless, a few hours running gives us six weeks of simulation time, and the atmosphere converges to the equilibrium state shown below, which you will find stored in SR_1200hr. The light gray cells are clouds of water droplets. The white cells are clouds of snowflakes. The dark gray cells are rain.



We see clouds of water droplets in the top row of cells. Here they are cooling by radiation. Our atmosphere is still opaque to long-wave radiation (transparency fraction is zero). Only the top cells can radiate into space. Their temperature is, however, well below 268 K (Tf_droplets), the temperature at which droplets are transformed into ice crystals. Snow forms within the clouds at 0.001 g/kg/s (freeze_rate_gps) and falls at 1 m/s (snow_speed_mps). When it sinks through a cell warmer than 278 K (Tm_ice), it melts at 0.01 g/kg/s (melt_rate_gps), forming rain. Rain falls at 5 m/s (rain_speed_mps).

The following graph shows how surface air temperature and average cloud depth vary with time from our cold start. The final cloud depth fluctuates by ±0.5 mm around an average value of 1.7 mm. The average temperature of the surface gas is 292 K, which is 19°C. Of the light that arrives from the Sun, 30% is reflected into space, giving our simulated planet an albedo of 0.3, which matches that of our own planet Earth.



With fast-sinking clouds, the cloud depth remained close to 2.9 mm and the surface temperature was −7°C. Evaporation from water at 19°C is roughly ten times faster than from from water at −7°C, but precipitation is so effective at removing water from the atmosphere, the sky is almost entirely clear. Indeed, the Sun shines directly upon our island half the time, heating its sandy surface up to 34°C.

Evaporation Cycle

The following diagram presents the simplified cycle of evaporation and precipitation we propose to implement in Circulating Cells Version 10.1.



Evaporation takes place from the sea, as before. When a body of moist air rises, it cools, and microscopic droplets form by condensation. Clouds of such droplets that happen to descend from above will warm up, and some or all of their droplets will evaporate. A cloud of droplets whose temperature drops below some threshold T_f will be transformed into snowflakes by the Bergeron Process, warming the surrounding gas with latent heat of fusion. We choose T_f several degrees below the freezing point of water, so we can assume the freezing takes place rapidly.

In our simulation, snow will fall at an average of 1 m/s, which we base upon our own observations. We will implement snow fall in the same way we implemented sinking clouds. Snow that reaches the surface will melt and thus take its latent heat of fusion from the surface block. This melting at the surface is the simplest way we can think of to conserve the latent heat of fusion of the water involved in our evaporation cycle. We assume that our surface water itself never freezes, no matter how cold it gets.

Our clouds, meanwhile, will no longer sink. Real cloud droplets are of order ten microns in diameter and sink at a few millimeters per second. The contribution of such sinking to our new cycle would be negligible.

Snow that enters a gas cell at a temperature greater than T_m will melt, cooling the surrounding gas by absorbing its latent heat of fusion. The melted snowflakes become raindrops a few millimeters in diameter, and these fall at 5 m/s. With the simulation set up as we have it now, the cells are around 400 m high, so rain will take a minute or two to fall out of one cell into the next. We will choose Tm several degrees above the melting point of water so we can assume the melting takes place rapidly.

Our simplified evaporation cycle omits many interesting evaporation-related phenomena. When rain drops are carried up into cold air, for example, they form hail, which later falls to Earth. When liquid rain falls into sufficiently dry air, it evaporates and disappears altogether, giving rise to virga. When air rises at just the right speed along a mountain slope, water droplets join together to form rain drops, as in orographic precipitation. Our simulation will contain none of these interesting phenomena. But we believe it will capture the fundamental features of the Earth's evaporation cycle, and so allow us to investigate how this cycle influences the global surface temperature.

Rain

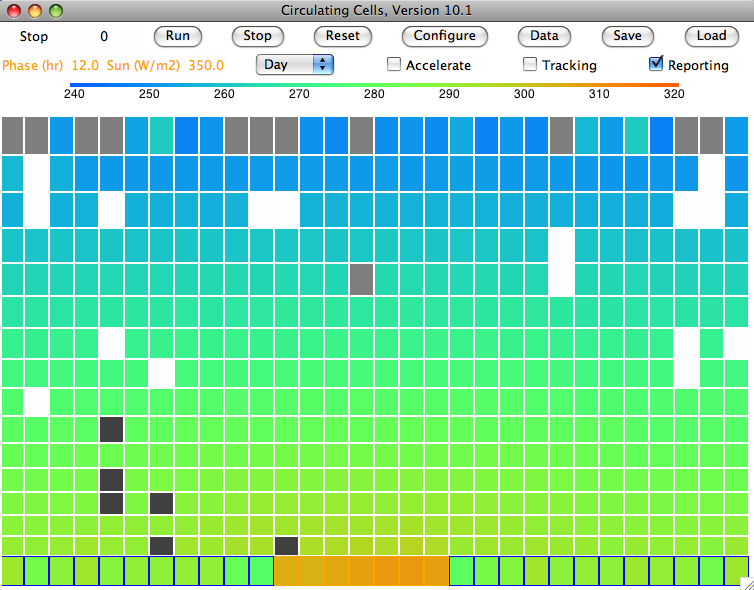
Our simulated sky never clears. Clouds fill the atmosphere almost entirely. They are forever forming in air that rises from the sea, and forever sinking to the ground, but they never come falling out of the sky all at once in the big drops we know as rain.

The droplets in our clouds are tiny. Those in our slow-sinking clouds are only 10 μm in diameter and descend at 3 mm/s. Those in our fast-sinking clouds descend at 300 mm/s. The graph we present in Falling Droplets implies that these fast-sinking droplets are 100 μm in diameter. Rain falls to Earth at several meters per second, so the same graph tells us that rain drops are at least 500 μm in diameter. A drop 500 μm in diameter contains a hundred times as much water as a droplet of 100 μm and a hundred thousand times as much water as a droplet of 10 μm. Could it be that cloud droplets collide and coalesce in order to form rain drops? If so, how long does this take, and under what circumstances does it occur?

The Wikipedia page on rain describes convective precipitation and orographic precipitation. In both these forms of rain, a cloud moves up, and encounters rain drops descending from above. If the descending drops are 500 μm in diameter, and the air is moving up at 1 m/s, the drops will remain at the same altitude. The cloud moving up and past them carries microscopic droplets that can collide with the stationary drops, coalesce with them, and so enlarge them until they are heavy enough to fall out of the rising cloud and descend to the Earth as rain.

But further reading suggests that rain formed of coalescing droplets is rare. A far more potent source of rain drops are ice crystals. In Cloud Physics, we learn of the Bergeron Process, whereby ice crystals grow, sink, melt, and become rain drops. Large rain-drops are melted hail-stones. Small rain-drops are melted snow-flakes.

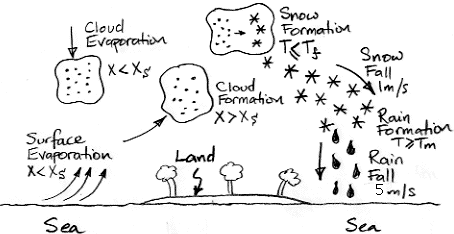
In our simulation, whenever the concentration of water vapor exceeds the saturation concentration, we assume the excess water condenses. It turns out, however, that the surface tension of liquid water makes it hard for water to condense into floating, microscopic droplets. If we provide a solid surface for the water to condense against, such as a blade of grass or a glass mirror, the water will condense when it reaches the saturation concentration, but in a body of air high above the ground, the only such surfaces would be dust particles, and these may be rare. Each one will serve as a catalyst for condensation until a droplet forms around it.

But the same is not true of ice crystals. In air saturated with water vapor and below the freezing point of water, an ice crystal can form on a grain of dust, and after that it will continue to grow. Water vapor deposits directly upon the surface of the crystal, thus changing state from gas to solid in one step, and the newly-created ice surface is an ideal foundation for further growth.

Now, suppose a cloud of microscopic water droplets rises until its temperature drops to −20°C. We might assume that the droplets will freeze. But pure water droplets resist freezing until they drop to −40°C. Ice crystals form in the midst of the cloud of super-cooled water droplets. As water vapor is deposited on the crystals, the concentration of water vapor in the air drops.

And here we encounter another curious physical phenomenon. The saturation concentration of water vapor with respect to an ice crystal turns out to be lower than the saturation concentration of water vapor with respect to super-cooled liquid water. Water vapor will deposit on the ice crystals until the concentration of water vapor drops to the saturation concentration of water vapor with respect to ice crystals. Because this concentration is below the saturation concentration with respect to super-cooled liquid water, the water droplets actually start to evaporate. The droplets evaporate, and their water is deposited onto larger and larger ice crystals.

Once the ice crystals are large enough, they start to fall, and they eventually fall into air that is warm enough to melt them. They turn into drops of water and fall to Earth as rain. It is this process that we will attempt to simulate in the next version of our Circulating Cells program.