Black Bodies

All objects that are above absolute zero temperature tend to radiate heat. The maximum amount of heat, P_BB that a body at temperature T can radiate per square meter of surface area is given by Stefan's Law.

P_BB = 5.7×10⁻⁸ T ⁴

(Note: Here we measure T in Kelvin, K. We have 0 K = −273°C and 0°C = 273 K. At 0 K an object has no heat at all, and therefore radiates no heat. The constant has units W/m²K⁴)

A body that radiates this maximum amount of heat is a black body. Such a body will radiate its power at a range of wavelengths as given by Plank's Law. The graph below shows the distribution of radiated power with wavelength for black bodies at 6000 K, which is the approximate temperature of the surface of the Sun, and 200 K, which is about as cold as it ever gets on the surface of the earth. The vertical axis is normalized power density, which we obtain by taking the power density at each wavelength and dividing by the maximum power density. The power density for a small range of wavelengths λ to λ+δ is the power radiated within this small range divided by the width of the range, δ, and so has units W/m²/m. Note that the wavelength axis has units μm but is plotted with a logarithmic scale.



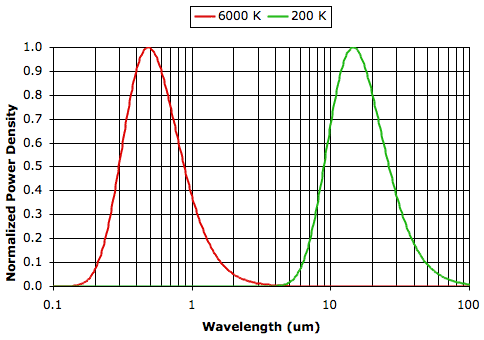
An object at 6000 K radiates 810,000 times as much power per square meter as an object at 200 K (−73°C). The graph shows how the 74 MW/m² emitted by an object at 6000 K and the 91 W/m² emitted by an object at 200 K are distributed with wavelength. The wavelength of greatest power emission is proportional to temperature, according to Wein's Displacement Law.

λ_max = 2.9×10³/T m.K

In Radiative Symmetry we showed how the Second Law of Thermodynamics dictates that a body's efficiency as a radiator at any particular wavelength is exactly matched by its efficiency as an absorber at that same wavelength. When a body absorbs all radiation of a particular wavelength we say it is black to that wavelength. A body that is black to a particular wavelength will radiate as much heat as a black body at that wavelength. A body that is transparent to a particular wavelength will radiate no power at that wavelength. A body that reflects half of a particular wavelength will emit half as much power as a black body at that wavelength.

The graph above shows that the peak emission wavelength for a body at 6000 K is 0.5 μm (green light), and for a body at 200 K is 15 μm (infrared). Almost all the power emitted at 6000 K lies between 0.2 μm (ultraviolet) and 2 μm (near infrared), and at 200 K lies between 6 μm (infrared) and 60 μm (far infrared).

If we want to determine graphically the proportion of power radiated in two or three different wavelength bands, we can count squares under a linear plot of power density, such as the one below for 6000 K, which is sunlight. You will find a similar plot for atmospheric temperatures here.



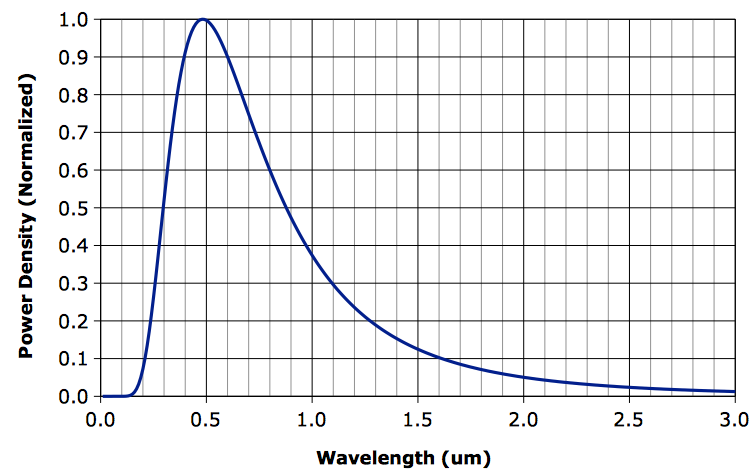
Visible light lies in the range 0.4 μm (royal blue) to 0.7 μm (ruby red). Counting squares under the graph, we find that roughly 15% of sunlight's power is in the ultraviolet, 40% is visible, and 45% is in the infrared.

In our next post we will consider how the atmosphere absorbs radiation from the earth but is transparent to radiation from the Sun, leading to the greenhouse effect.