Extreme Greenhouse

We continue our consideration of the atmospheric greenhouse effect with an extreme example, in which we maximize the effect. The diagram below shows the surface of a body which is covered by vacuum, surrounded by a filter, and illuminated by a sun. By virtue of its high surface temperature, the sun emits short-wave radiation, let us say, between 0.2 μm and 2 μm, while the body, by virtue of its lower surface temperature, emits long-wave radiation, let us say, between 6 μm and 30 μm. (See our earlier Black Bodies post for explanations of these wavelengths.)

The filter is so-called because it allows short-wave radiation to pass through without loss, but absorbs all long-wave radiation immediately upon entering. By radiative symmetry, the filter cannot radiate at all at short wavelengths, but is a perfect radiator of long wavelengths. The body itself we assume is a perfect absorber of short-wave radiation and a perfect emitter of long-wave radiation. Which is to say: it is black to both short-wave and long-wave radiation.



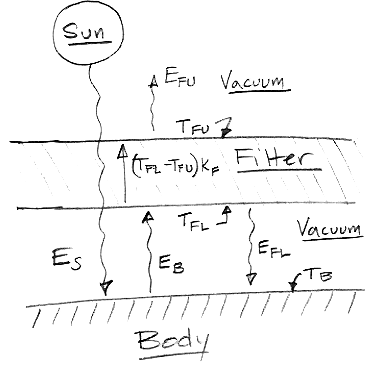
The squiggly lines are radiation, denoted E with an appropriate subscript: S for sun, B for body, FL for filter lower surface, and FU for filter upper surface. We measure radiation in units of W/m². We have temperatures marked also, denoted T. There is heat flow by conduction within the filter, amounting to K_F(T_FL−T_FU), where _F is the conductivity of the filter in W/Km². The only heat flow from the body to the filter is by radiation, because the two are separated by a vacuum.

We assume that all parts of our system are in thermal equilibrium, which is to say that their temperature is constant, so that there is as much heat leaving them as entering them. We assume there is no way for heat to leave the body except through its top surface, which would be the case if the top surface wrapped around upon itself as does the surface of a sphere.

Let's start with the simple case where the filter is a perfect conductor, so that T_FL = T_FU (K_F is infinite). The top and bottom surfaces are black-body radiators, so they both emit the same amount of long-wave radiation. Thus E_FL = E_FU. Meanwhile, we must have as much heat leaving our system as entering, so E_S = E_FU. At the same time, we must have equal heat entering and leaving the body itself, so E_S + E_FL = 2E_FL = E_B. The power radiated by the body is a factor of two greater than the power arriving from the sun.

Radiated power is related to temperature by Stefan's Law. With σ as Stefan's constant, we have E_B = σ(T_B)⁴ = 2E_FL = σ(T_FL)⁴, from which we conclude T_B = 2^1/4T_FL = 1.19T_FL. But T_FL = T_FU, and we can determine T_FU by noting that E_S = E_FU = σ(T_FU)⁴, which yields T_FU = (E_S/σ)^1/4. As we showed in Solar Heat, in the case of the Sun and the Earth, we have E_S = 350 W/m². With 350 W/m² arriving from the sun, we would have, in our example construction, T_FU = 280 K = 7°C and T_B = 333 K = 60°C. The presence of the filter raises the temperature of our body by 53°C.

The greenhouse heating of a black body when we place a perfectly-conducting greenhouse filter between the body and a source of short-wave radiation is 19% of its equilibrium absolute temperature without the filter. Furthermore, in these particular circumstances, the heat radiated by the warmed body is exactly twice that radiated into space by the filter, and twice that received from the source of short-wave radiation.