Conclusion

The anthropogenic global warming (AGW) hypothesis presented by the majority of today's climatologists has two parts. First it claims that the world is getting exceptionally warm, and second it claims that human carbon dioxide (CO2) emissions are the cause of this warming. Seven years ago, we began our personal investigation of this hypothesis, and we did so by considering whether or not the world was indeed getting exceptionally warm.

The first thing we did was estimate the uncertainty inherent in the measurements of global surface temperature. We concluded that natural variations in local climate introduce an error of roughly 0.14°C in the measurement of the change in temperature between any two points in time. The fact that the error is constant with the time over which we measure the change is a consequence of the particular characteristics of local climate fluctuations.

We downloaded the weather station data from NCDC and calculated the global surface anomaly using a method we called integrated derivatives, but which others have called first differences. The graph we obtained was almost identical to the one obtained by CRU using their complex reference grid method. It remains a mystery to us why institutions like CRU, NASA, and NCDC use such a complex method when a far simpler one will do. All graphs show roughly a 0.6°C rise in global surface temperature from 1950 to 2000. This rise is significant compared to our expected resolution of 0.14°C.

We made this plot superimposing the number of weather stations and the global surface anomaly versus time. The number of weather stations drops dramatically from 1960 and 1990. Only one in four remain active at the end of this thirty-year period. During the same period, the global surface anomaly shows a 0.6°C rise. By selecting subsets of the weather stations, we found that the apparent warming from 1950 to 1990 varied from 0.3°C to 1.0°C depending upon whether we used stations that disappeared in that period, persisted through that period, or existed shorter or longer intervals in the same century. Thus is seemed to us that some significant amount of work would have to be done to eliminate the change in the number of weather stations as a source of error in the data. But we saw no mention whatsoever of this source of error in published papers in which the global surface anomaly is presented, such as Jones et al..

We plotted a global map of the available weather stations, color-coded to show the date they first started reporting. The map shows that almost all stations in the tropics began operating after 1930, while most of those in the temperate regions were operating by 1880. This seems to us to be another source of systematic error in our measurement of the global surface anomaly.

Weather stations might also be affected by the appearance of buildings, tarmac, and road traffic. We found examples of weather stations in which such urban heating caused an apparent warming of several degrees centigrade over a few decades. It seemed to us that this effect would have to be examined in depth by any paper presenting a global surface trend. But papers such as Jones et al. do not address the urban heating issue directly. Instead, they claim that the effect is negligible and refer to other papers as proof. But when we looked up those other papers, we did not find any such proof.

In order to argue that modern temperatures were exceptionally warm, climatologists produced the hockey stick graph, in which a collection of potential long-term measurements of global surface temperature were combined together under the assumption that they could be trusted only to the extent that they showed a temperatures increase from 1950 to 2000. Indeed, if a measurement showed a temperature decline in that period, the hockey stick method would flip the trend over and add it to the combination so that it now contributed to a rise in the same period.

The hockey-stick graph shows no sign of the Medieval Warm Period, in which Greenland was inhabited by farmers, nor the Little Ice Age, when the Thames was known to freeze over, and nor should we expect it to. Given a random set of measurements, the hockey-stick combination method will almost always produce a graph that shows a sharp rise from 1950 to 2000 and a gentle descent during the thousand years before-hand. When applied to the existing measurements of temperature by tree rings, ice cores, and other such indirect methods, it is no surprise that the method produced that same shape.

We presented our doubts about the surface temperature measurements and the hockey stick graph to believers in the AGW hypothesis. We were received with disdain and given no satisfactory answers. Furthermore, the Climategate affair revealed several significant breaches of scientific method by the climate science community. For example, in this graph produced by climatologists for the World Health Organization, the authors removed the tree ring temperature data from 1960 onwards because it showed a decline in temperature, and substituted temperature station measurements in their place. They plotted the combination as a single line. When I asked a prominent climatologists what exactly had been done, he said, "The smooth was calculated using instrumental data past 1960." He declared that a better way to handle the divergence of the tree-ring data from the station measurements would be to cut short the graph of tree-ring data at 1960, so as to hide the decline in temperatures measured by the tree rings.

What we see here is the assumption by climatologists that the world has been warming up and that the global temperature measured by weather stations is correct. This assumption leads them to delete conflicting data on the grounds that it must be bad data. Thus it becomes impossible for them to discover that their assumption is incorrect. By this time, we were skeptical of the global surface anomaly we obtained from the station data. We were no longer certain that the data itself had not been modified by NCDC. We had little reason to trust any other measurement produced by climatologists, we were unimpressed with the hockey-stick method of combining measurements, and we were quite certain that recent temperatures were not exceptional for the past ten thousand years.

We turned our attention to the second part of the AGW hypothesis: the one that says doubling the atmosphere's CO2 concentration will increase the surface temperature by roughly 3°C. It took us a long time to come to a conclusion on this one. The climate models upon which such predictions are based are private property of various climatologists. In any event, we do not trust models produced by a community that is willing to delete data that conflict with its assumptions. If they are willing to delete data, we must assume that they are willing to adjust their models until the models give predictions consistent with their AGW hypothesis.

We began with some laboratory experiments on radiation. We stated the principle of the greenhouse effect. After a great deal of searching around, we eventually obtained the absorption spectrum of various layers of the Earth's atmosphere. This allowed us to confirm that, if the skies remained clear, a doubling of CO2 concentration would cause the world to warm up by about 1.5°C.

But of course the skies don't remain clear. The formation of clouds is a strong function of surface temperature. If the world warms up, there will be more clouds. They will reflect more of the Sun's light, while at the same time, slowing down the radiation of heat into space by the Earth. To determine how these two effects would interact, we built our own climate model, which we called Circulating Cells.

When it comes to determining the effect of increased cloud cover, the most critical parameter to decide upon is the reflection of sunlight by clouds per millimeter of water depth in the cloud. It seemed to us that there should be a large body of literature written recently upon this subject because it is so important to climate modeling. The best paper we found upon the subject was written in 1948, Reflection, Absorption, and Transmission of Insolation by Stratus Cloud. We found a couple of more recent papers about reflection, such as this one, but they do not attempt to provide an empirical formula for the reflection of clouds with increasing cloud depth. We concluded that climatologists are not examining this issue in detail.

In a long sequence of small steps, we built up our climate model until it implemented surface convection, surface heat capacity, evaporation, cloud formation, precipitation, and radiation by clouds. We tested every aspect of the simulation in detail, and based its operating parameters upon our own estimates and upon whatever measurements we could find in climate science journals. We did not choose our model parameters to suit any hypothesis of our own, nor could we have done, because we did not have a model capable of testing the AGW hypothesis until the final stage, and we did not change the parameters in that final stage.

The latest version of our climate model shows that cloud cover increases rapidly as the surface warms above the freezing point of water. The evaporation rate of water from the surface increases approximately as the square of the temperature above freezing, and the only way for water to return to the surface is to form a cloud first. If we ignore the increased reflection of sunlight due to increasing cloud cover, and consider only the slowing-down of radiation into space by the same increase in cloud cover, our model shows roughly 3°C of warming due to a doubling in CO2 concentration. But when we take account of the increased reflection of sunlight by the increasing cloud cover, the warming drops to 0.9°C.

It seems to us that the climate models used by climatologists ignore the reflection of sunlight due to clouds. They may allow for some fixed fraction of sunlight to be reflected by clouds, but they do not allow this fraction to increase with increasing surface temperature. Thus they conclude that the warming due to CO2 doubling will be 3°C. If they took account of the increased reflection, the effect would be far smaller and less dramatic: roughly 1°C.

Doubling the CO2 concentration of the atmosphere will indeed encourage the world to warm up, but not by enough that we should worry. Right now CO2 concentration has increased from roughly 300 ppm to 400 ppm in the past century. If it gets to 600 ppm then we can say that the rise in CO2 concentration will tend to warm the Earth by 1°C. But we are unlikely to be able to check our calculations, because the natural variation in the Earth's climate is itself of order ±1°C from one century to the next.

And so we find ourselves at the end of our journey. Modern warming is not exceptional, and doubling the CO2 concentration will cause the world to warm up by roughly 1°C, not 3°C. The only part of the AGW theory we have not investigated is its assertion that human CO2 emissions are responsible for the increase in atmospheric CO2 concentration over the past century.

My thanks to those of you who took part in the effort, both by private e-mails and in the comments. I would not have continued the effort without your participation. I hope it is clear that my use of "we" instead of "I" is in recognition of the fact that this has been a group effort. I will continue to answer comments on this site, and I will consider any suggestions of further work. To the first approximation, however: we're done.

Anthropogenic Global Warming

The Anthropogenic Global Warming (AGW) hypothesis states that doubling the CO2 concentration of the Earth's atmosphere will raise the average surface temperature of the Earth by a minimum of 1.5°C, and more likely 3°C.

In our investigation of the absorption and emission of long-wave radiation by the Earth's atmosphere, we calculated that a sudden doubling of CO2 concentration would decrease the power the Earth radiates into space by 6.6 W/m². We then estimated how much the Earth and its atmosphere would have to warm up in order to restore the heat radiated into space to its original value. We assumed there would be no significant change in cloud cover as a result of the warming, and we applied Stefan's Law to calculate how the heat radiated by the Earth and its atmosphere would increase. We found that the required increase in surface temperature would be around 1.6°C. If there were no change in cloud cover, then the heat arriving from the Sun would remain the same, and we could expect the Earth to warm up by 1.6°C so as to once again arrive at thermal equilibrium.

The AGW hypothesis states that in the event of the Earth warming, changes in cloud cover will be such as to amplify the warming we calculate using Stefan's Law. Here is an extract from today's entry on Global Warming at Wikipedia.

The main positive feedback in the climate system is the water vapor feedback. The main negative feedback is radiative cooling through the Stefan–Boltzmann law, which increases as the fourth power of temperature.

As the Earth warms up, water evaporates more quickly from the oceans. Almost all water that evaporates must turn into clouds before it returns to Earth. Water condensing directly onto grass in the morning is an exception to this rule, but the vast majority of water vapor will return only as rain or snow, and so must first take the form of a cloud.

Clouds absorb long-wave radiation emitted by the Earth's surface, so the Earth cannot radiate its heat directly into space. Instead, the clouds radiate into space and warm the Earth with back radiation. Thus increasing cloud cover means less heat radiated into space for the same surface temperature. This is the positive feedback referred to by the AGW hypothesis. The AGW climate models predict that this positive feedback will amplify the minimum 1.5°C warming caused by CO2 to roughly 3°C. Some say 2°C and other say 4°C, but all agree that the actual warming will be greater than 1.5°C.

We see this positive feedback in our Circulating Cells simulation, version CC11, which simulates the formation of clouds as well as their absorption and emission of long-wave radiation. The graph below shows a close-up of the behavior of the simulation in the neighborhood of its equilibrium point for 350 W/m² solar power.



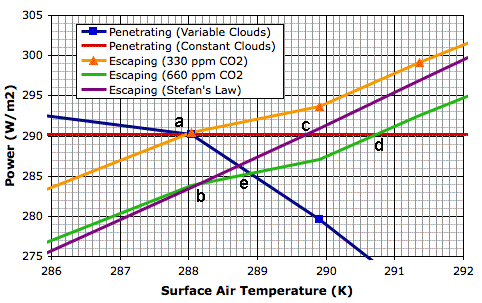
The blue line shows how the power that penetrates to the surface of our simulated planet varies with increasing surface temperature. The orange line shows how the total power escaping from our simulated planet increases with surface temperature. These two lines cross at a, where temperature is 288 K and total escaping power is 290 W/m². Our simulated atmosphere absorbs 50% of long-wave radiation, which is an adequate approximation of our atmosphere with its current concentration of CO2 (roughly 330 ppm).

The green line is the same as the orange line, but displaced down by 6.6 W/m², which is the amount by which we calculated the total power escaping from the Earth will decrease if we double CO2 concentration (to roughly 660 ppm). Thus the green line tells us the total escaping power at the same temperature if we were to double the CO2 concentration. Point b on the green line is 288 K, and the total escaping power is 283.4 W/m².



The purple line shows how the total escaping power will increase from b if we assume the cloud cover is constant and use only Stefan's Law to determine the heat radiated into space by the surface and atmosphere. The red line shows the solar power penetrating to the surface if we assume the cloud cover is constant. With constant cloud cover, the penetrating solar power does not change.

The purple and red lines meet at c, which is 289.6 K, or 1.6°C above the previous equilibrium point. Thus our simulation shows us that the warming due to CO2 doubling, if we ignore changes in cloud cover, will be 1.6°C, which is consistent with our previous calculation.

The green line, however, is the simulation's calculation of the total escaping power for increasing surface temperature. We see that the heat radiated into space does not increase as quickly as Stefan's Law would lead us to expect. And the reason for that is precisely the reason quoted by the AGW hypothesis: increasing cloud cover is slowing down the radiation of heat into space. The green line and the red line intersect at d, which is 290.7 K, or 2.7°C above our original equilibrium temperature. This is the new equilibrium temperature of the planet surface if we double CO2 concentration and we assume that there will be no change in the solar power penetrating to the surface while the cloud cover increases.



But the solar power penetrating to the surface must decrease as cloud cover increases. Clouds reflect sunlight. Thick clouds reflect 90% of solar power back into space. Even thin, high clouds reflect 10%. Increasing cloud cover will decrease the solar power penetrating to the surface. That is why our blue line slopes downwards. This is negative feedback, which acts against the positive feedback described by the AGW theory. The blue line shows how the solar power penetrating to the surface decreases as our cloud cover increases.

The blue line and the green line intersect at e, which is the equilibrium point we arrive at after doubling the CO2 concentration and considering both the positive feedback of back-radiation and the negative feedback of solar reflection. The temperature at e is 288.9 K, which is 0.9°C above our original equilibrium temperature.

Thus our simulation shows how the negative feedback generated by clouds dominates their positive feedback, and suggests that the actual warming of the Earth's surface due to a doubling of CO2 will be closer to 0.9°C than the 3°C predicted by the AGW hypothesis.

Equilibrium Point

Heat arrives at the Earth in the from of sunlight. The clouds reflect some of it. Almost all the rest arrives at the Earth's surface. Of the sunlight that reaches the surface, some is reflected back into space, especially by snow, but most is absorbed. To the first approximation, therefore, sunlight affects the climate only by it warming the surface, not by warming the atmosphere directly.

In our Circulating Cells simulation, version CC11, solar power is either reflected by clouds or absorbed by the surface. The only way for heat to enter the atmosphere is by contact with the surface, so it is the temperature of the surface that drives the the circulation of gases and the creation of clouds, snow, and rain. When we observe, for example, that 80% of solar power is penetrating to the surface when the surface gas temperature is 290 K, we can assume that the 80% of solar power will penetrate to the surface whenever the surface gas temperature is 290 K.

Our program of solar increase provides us with observations of cloud depth and penetrating power for a range of solar powers, and therefore for a range of surface temperatures. The following graph shows how the fraction of solar power penetrating to the surface varies with surface temperature.



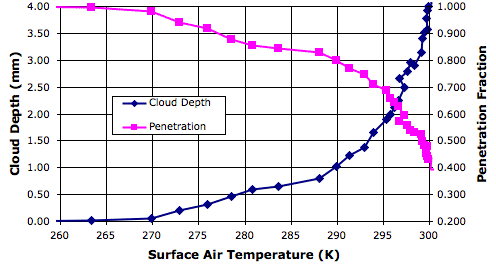
In our simulation we calculate the penetrating power for each surface block using the depth of the clouds in the column of cells above the surface block. We cannot, however, use the average cloud depth to obtain a measurement of average penetration fraction. When we do so, our measurement is always too low, because there are gaps in the cloud cover, and these gaps allow more light to pass through than if the clouds were distributed uniformly.

In the following graph, we have taken our measurements of penetration fraction and used them to calculate the power that would penetrate to the surface for two values of solar power: 350 W/m² and 400 W/m². Along with these penetrating powers, we also plot the total escaping power.



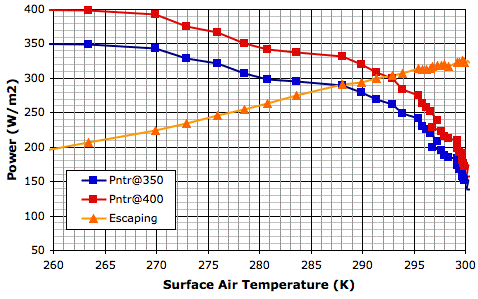
At thermal equilibrium, the total escaping power must be equal to the penetrating power. Thus the intersection of the penetrating power and escaping power graphs occurs at the equilibrium temperature. For solar power 350 W/m², the intersection occurs at 288 K. For 400 W/m², the intersection occurs at 292 K. These are, of course, the same equilibrium temperatures we obtain from our existing graph of surface temperature versus solar power.

In our next post, we will use the above graph and the calculations we presented in With 660 PPM CO2 to estimate how much the Earth would warm up if we doubled the CO2 concentration of its atmosphere.

Conservation of Heat

In Solar Increase we were concerned that our program of increasing solar power did not allow adequate time at each value of solar power for the simulation to arrive at thermal equilibrium. As we described in our previous post, we now have measurements of the state of the simulation at each value of solar power. The following graph plots penetrating power, total escaping power, and downwelling power versus solar power. The penetrating power is the power per square meter that gets to the surface through the clouds. The total escaping power is the power per square meter that the surface and atmosphere together radiate into space. The downwelling power is the power arriving back at the surface from the radiating clouds.



The downwelling power is increasing because the cloud layer is getting thicker. The clouds radiating heat towards the surface are lower down and therefore warmer. But it is the equality of the penetrating and escaping power that interests us the most today. At thermal equilibrium, the total escaping power should be equal to the penetrating power. And indeed we see that this appears to be the case for all values of solar power.

Thickening Clouds

As we describe in Solar Increase, we warmed up our simulated planet by increasing the incoming solar power by 10 W/m² every two thousand hours of simulated time. Starting from an initial value of 100 W/m², we increased the solar power to 1200 W/m² over the course of three weeks of our own time, which corresponds to the passage of over a million hours of simulated time. During the course of the simulation, we recorded the state of the atmospheric array every twenty hours, and these recordings constitute our measurements of the simulated atmosphere during the course of our simulated experiment.

In our pervious post we observed that some properties of the atmosphere, such as penetrating power, fluctuated greatly from one measurement to the next. In order to reduce the influence of these fluctuations, we took the average of the last 500 hours of measurements at each value of incoming solar power, and so obtained a value for each property at each solar power. The graph below shows how some of these properties vary with solar power.



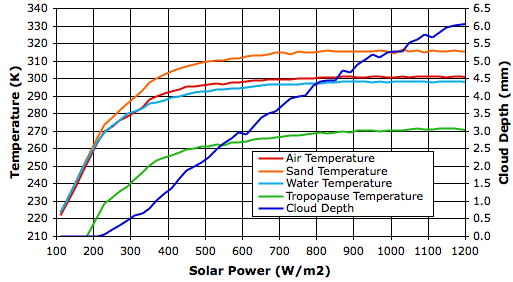
Surface temperature increases hardly at all from 800 W/m² to 1200 W/m², and yet cloud cover increases steadily. How can it be that cloud cover increases when the surface temperature, which drives evaporation, hardly increases at all?

In our simulated evaporation cycle, precipitation beings with the formation of snow in air below temperature Tf_droplets. We have this parameter set to 268 K, which is five degrees below the freezing point of water. When solar power reaches 800 W/m², the average temperature of the tropopause has reached 268 K. Snow can form only in the colder clouds of the tropopause, and nowhere below the tropopause. Each time we increase the solar power, the surface temperature at first warms a little, but within a few hundred hours, this warming reaches the tropopause, where it further slows snow formation, and increases the cloud depth. With more sunlight being reflected back into space, the surface cools again until it is hardly warmer than it started. For solar powers greater than 800 W/m², an increase of 100 W/m² causes a substantial increase in cloud depth (roughly 0.5 mm), a slight increase in tropopause temperature (roughly 1 K), and an increase in surface temperature too small for us to detect (less than 0.3 K).

This profound suppression of warming by our simulation is not, however, a good representation of what would happen in the Earth's atmosphere. In our simulation, gas cells that contain clouds cannot rise above our top row of cells, so there is a limit to how much they can cool down. In the Earth's atmosphere, clouds can rise as far as they need to in order to cool down and produce snow rapidly. Thus our simulation is no longer realistic once its tropopause approaches the melting point of ice. We will therefore concentrate our attention upon the behavior of the simulation for solar powers less than 600 W/m², for which our simulated tropopause is well below the temperature required for the rapid formation of snow.

Solar Increase Continued

Today we continue our previous post without any preamble. The graph below shows how our simulated atmosphere warms up as we increase the solar power from one hundred to twelve hundred Watts per square meter. The green line shows how we increased the solar power over the course of twelve simulated years. The blue line shows how the power penetrating to the surface varied with time. The red line is the average temperature of the air resting upon the surface of our simulated planet.



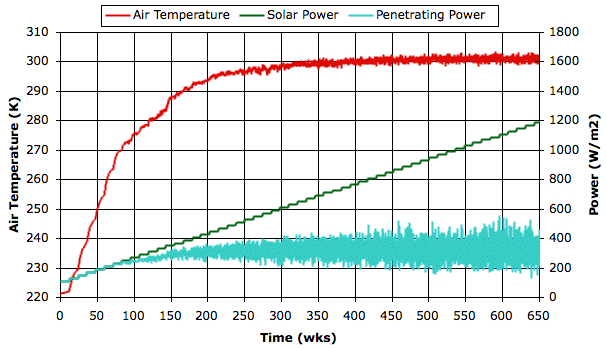
At first, when the sky is clear, the solar power and the penetrating power are equal. But when the solar power reaches 300 W/m² clouds form and the penetrating power drops below the solar power. As solar power increases from 600 W/m² to 1200 W/m², fluctuations in the penetrating power double in their extent, but the average penetrating power appears to remain unchanged. The negative feedback generated by the evaporation cycle is so powerful that the surface air temperature increases by only a few degrees while we double the solar power.

The following screen shot shows the state of the simulation after two thousand hours at 1210 W/m². You can download this state as a text file SIC_1210W and load it into CC11 to watch the vigorous formation of clouds and descent of precipitation.



We now have the data we need to plot graphs of surface temperature and other properties of the simulation versus solar power.

Solar Increase

In our previous post we cooled down our simulated atmosphere by reducing the incoming solar power to 100 W/m². We gave the simulation plenty of time to reach equilibrium, and it arrived at the state RC_100W. The sky is clear. All the Sun's power penetrates to the surface. The surface temperature is −50°C.

We started CC11 from this equilibrium state. We increased the solar power to 110 W/m². After two thousand hours of simulated time, we increased the solar power to 130 W/m². We ran for another two thousand hours of simulated time, after which we increased the solar power again. The program performs the solar Increases automatically, so we were able to walk away from the computer and let the simulation run on its own.

The following graph shows surface temperature and solar power plotted against simulation time in weeks. The purpose of this plot is to determine if our simulation reaches equilibrium at each value of solar power.



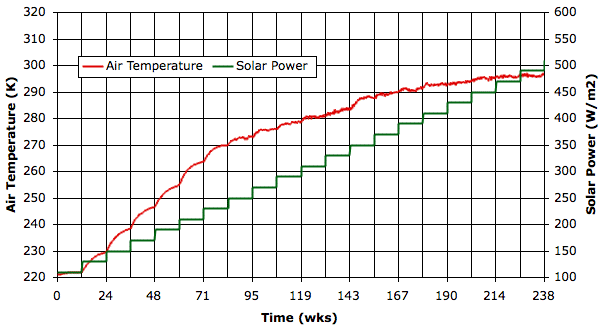
Below 270 K, we see see the surface temperature is still increasing two thousand hours after the increases in solar power. Perhaps ten thousand hours at each step would be enough. But we are faced with a practical problem of execution time: it took one full week for us to obtain the graph above, with a computer dedicated to the job running continuously.

Once the surface temperature gets above 270 K, however, the evaporation cycle starts up and we see the effects of negative feedback. The changes that result from increases in solar power are markedly smaller and they establish themselves more quickly. Thus our program of solar Increase appears to be gradual enough for temperatures above 270 K, and these are the temperatures we are most interested in.

The following figure shows the equilibrium state of the atmosphere with 490 W/m² solar power. The running simulation shows vigorous cloud formation and precipitation. You can view this for yourself by downloading CC11, loading state SI_490 into the program, setting Q_sun to 490 in the configuration panel, and pressing Run.



By next week, we hope to have obtained the equilibrium state of our simulation for solar powers 100 W/m² all the way up to 900 W/m².

A Big Chill

In Negative Feeback, we increased our simulation's incoming solar power from 200 W/m² to 400 W/m² and saw the surface warm by only a 5°C. It turned out that the increasing solar power was almost entirely compensated for by an increase in cloud thickness, so that the power penetrating to the surface remained almost constant. We now ask ourselves, what will happen if we drop the solar power all the way down to 100 W/m²? Will our Radiating Clouds be able to stop the world from cooling?

We started our Circulating Cells program (CC11) in its equilibrium state for 350 W/m² solar power (RC_14000hr), and reduced the solar power to 100 W/m². The following graph shows surface air temperature and atmospheric cloud depth for the first five hundred hours.



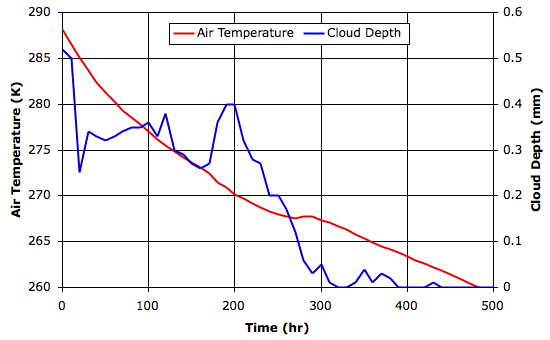
In the first ten hours, the surface temperature drops by a few degrees. This is what we might expect during one of Earth's nights. After three hundred hours, the surface temperature has dropped to −5°C and there are hardly any clouds left in the sky. The following graph shows the world cooling down to a new, clear-sky equilibrium of −50°C. The graph also shows the solar power penetrating to the surface. Once the sky clears, the penetration is exactly equal to 100 W/m². We saved the final state of the atmosphere in RC_100W.



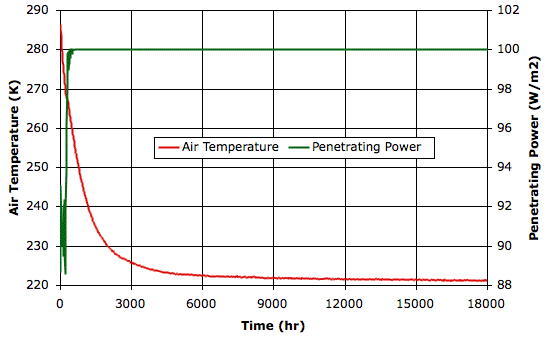
We conclude that 100 W/m² is insufficient solar power to warm the Earth above the freezing point of water, and therefore insufficient solar power to generate the cycle of evaporation and precipitation that stabilizes our climate.

Lapse Rate

Our Radiating Clouds simulation uses 350 W/m² for incoming solar power. We know from our Solar Heat calculation that this is the average power arriving at the Earth from the Sun. Our hope is that the lapse rate and surface temperature of our simulation will agree well with the actual lapse rate and surface temperature of the Earth's atmosphere. In the design of our simulation, however, we have made no effort to adjust its parameters to bring about such an agreement.

In the figure below, the blue graph shows temperature versus altitude for thermal equilibrium in the wet atmosphere of our Radiating Clouds simulation. We loaded the equilibrium state, RC_14000hr, into CC11 and instructed the simulation to print temperatures and altitudes.



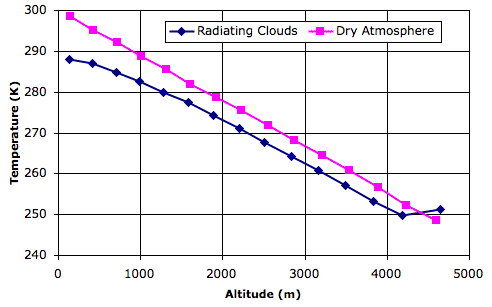
For comparison, we went back to Simulated Planet Surface and loaded the equilibrium state, Day_4, which arises with the same solar heat, but with the surface entirely made of sand. Thus the pink graph shows temperature versus altitude in a dry atmosphere.

The equilibrium state of the dry atmosphere, which looks like this, shows a linear drop in temperature with altitude. According to our calculations, this slope should be −g/Cp, where g is gravity and Cp is the specific heat capacity of the dry gas. Our simulation uses 10 N/kg for gravity and 1003 J/K for Cp, so the slope of the pink graph should be close to −0.010 K/m. Its actual slope is −0.011 K/m.

The equilibrium state of the wet atmosphere, which looks like this, shows a linear drop in temperature only between altitudes 2 km and 4 km. Near the surface of the planet, the heat liberated by condensing water vapor into rising air reduces the amount by which air cools as it rises. In the tropopause, radiation from the planet surface is absorbed by the tropopause clouds, causing them to be warmer than the air immediately below. In the linear region of the graph, the slope is −0.011 K/m, but if we simply divide the total drop in temperature by the altitude of the tropopause, we obtain a net slope of −0.008 K/m.

Looking at graphs such as these, it appears that the Earth's atmosphere has a lapse rate of around −0.0065 K/m. Our simulation does not come up with this lapse rate exactly, but we see that the introduction of water does cause a substantial reduction in the net lapse rate, and with this we are well-satisfied.

The average temperature of the surface of the Earth is around 14°C, or 287 K. This is the average temperature of the air just above the planet surface, not the temperature of the surface itself. The thermometers we use to measure the surface temperature are several meters above the ground. When we use dry air and a sandy surface in our simulation, the average temperature of the surface air is 298 K. But when we add radiating clouds, rain, and snow, the average temperature drops to 288 K, or 15°C. We are well-satisfied with this agreement also.

Thermal Equillibrium

An object is in thermal equilibrium when the amount of heat entering the object is equal to the amount of heat leaving it. In the case of a planetary system, consisting of a surface and atmosphere, the system will be in thermal equilibrium when the heat arriving from the Sun is, on average, equal to the heat the system radiates into space. The planetary system of our Circulating Cells program will be in thermal equilibrium when the short-wave radiation penetrating to the planet surface from the Sun is balanced by the long-wave radiation escaping into space from its surface, atmospheric gas, clouds, rain, and snow.

When our simulated system converges upon a state where the temperature of its surface and of its atmospheric layers fluctuates around some average value, our hope is that the heat penetrating to the surface from the Sun will be equal, on average, to the heat the system radiates into space. The heat penetrating from the Sun is, of course, the incoming short-wave radiation that is not reflected back into space by our simulated clouds. The heat radiated into space is the upwelling radiation at the top of our simulated atmosphere. We refer to the top of the atmosphere at its tropopause, and to the heat radiated into space as the total escaping power.

We instructed CC11 to print out the average penetrating power from the Sun and the total escaping power from the tropopause every ten hours, and plotted these values for the fourteen thousand hours of the experiment we performed in our previous post. For the final ten thousand hours, the temperature of the surface and the atmospheric layers fluctuate by ±1°C around their average values, as you can see here.



Over the final ten thousand hours, the average penetrating power is 290.0 W/m² and the average escaping power is 289.6 W/m². Given the size of the fluctuations in both quantities, and the errors introduced by certain simplifications in our simulation's calculations, we are well-satisfied with this agreement. Our simulation converges upon an equilibrium state that is also a state of thermal equilibrium.

Radiating Clouds

The latest version of Circulating Cells implements the upwelling and downwelling radiation calculations we described in Up and Down Radiation. To run the program, download CC11 and follow the instructions at the top of the code. Clouds absorb and emit long-wave radiation as if they were black bodies. We now set the transparency fraction of our atmospheric gas to 0.5, so that it will be transparent to half the wavelengths in the long-wave spectrum and opaque otherwise. The planet surface can radiate heat directly into space at these transparent wavelengths, as it did in Simulated Planet Surface. But now we have clouds doing the same thing, while at the same time reflecting sunlight back into space.

We begin our simulation with the final state of Simulated Rain, which you will find in SR_1200hr. The initial surface air temperature is 292 K, and cloud depth is 1.5 mm. The following graph shows how air temperature and cloud depth vary in the first two thousand hours.



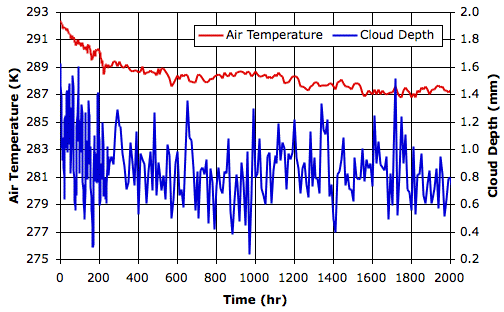
The following graph shows the first fourteen thousand hours. You will find the final state of the array in RC_14000hr. The average surface air temperature over the final ten thousand hours is 288 K, and the average cloud depth is 0.8 mm.



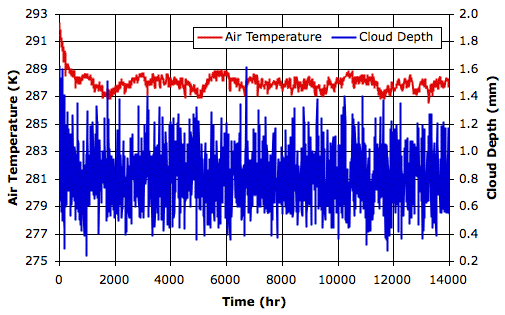
During the course of these fourteen thousand hours, the distribution of clouds in the atmosphere varies greatly. Sometimes there is a layer of clouds just above the surface of the sea. At other times there are clouds along much of the tropopause. For a view of the final state of the simulation, see here.

As we have discussed many times before, the absorption of long-wave radiation by the atmosphere gives rise to the greenhouse effect. The more opaque the atmosphere, the more heat must be radiated into space by the tropopause instead of the planet surface. In order to radiate more heat, the tropopause must be warmer. If the tropopause is warmer, the planet surface must be warmer too, in order to motivate convection to carry heat to the tropopause. When we change our atmospheric gas from 0% to 50% transparency, we expect the surface temperature drop. And indeed it does: by 4°C.

This cooling of 4°C is, however, far less than the cooling of 31°C we observed when we increased the transparency of our gas from 0% to 50% in the absence of simulated clouds. As we have already discussed, clouds and rain greatly reduce the sensitivity of surface temperature to changes in solar power. Now we find that they also greatly reduce the sensitivity of surface temperature to changes in the transparency of the atmospheric gas.

Up and Down Radiation

We are going to add to our Circulating Cells simulation the absorption and emission of long-wave radiation by clouds. As we showed earlier, a liquid water depth of 100 μm absorbs over 99% of all long-wave radiation. Rain contains liquid water also, and ice is a good absorber of long-wave radiation too. We will add the equivalent depth of snow, rain, and cloud droplets for each cell, and so obtain the depth of water within the cell that acts to absorb long-wave radiation.

We note that the same addition of rain, snow, and cloud droplets does not apply to the transmission of short-wave radiation. Water is transparent to short-wave radiation, and clouds reflect it by refracting it through millions of microscopic droplets. But rain and snow contain thousands of times fewer drops and crystals for a given depth of water, so they are thousands of times less effective at refracting sunlight.

For simplicity, we will assume the water in a cell is either transparent or opaque to long-wave radiation, but not in-between. If the combined concentration of rain, snow, and cloud droplets in a cell is greater than wc_opaque, we will assume the entire gas cell is opaque to long-wave radiation. Otherwise, the cell will absorb long-wave radiation as if it were dry, as determined by our transparency_fraction. With our 300-kg cells, a concentration of 0.33 g/kg corresponds to 100 μm of water.

Now we are faced with the possibility of multiple layers of cloud, snow, and rain, all absorbing and emitting long-wave radiation in all directions. The first simplification we make is to assume each gas cell radiates only vertically upwards and downwards. Because our columns of cells are much the same as one another on average, the net effect of this simplification will be small. Even with this simplification, we see that a cloud can absorb radiation from a cloud below, and emit radiation back to that same cloud below, and upwards to a third cloud.

We will calculate the effect of long-wave radiation in the following way. We start at the surface and allow it to radiate as a black body. We allow this upward radiation to enter the first gas cell. We calculate how much is absorbed by the cell and how much keeps going. We calculate how much power the gas cell itself radiates upwards. We add this to the existing upward radiation. We move on to the cell above, and so on, until we get to the tropopause. At the tropopause, we assume the atmosphere above is transparent to long-wave radiation, so all upward-going radiation passes out into space.

We repeat the same process, going down. We start with the tropopause gas cell in each column and move down cell by cell until we arrive at the bottom, at which point all the downward-going radiation is absorbed by the surface. We first considered this kind of downward-going long-wave radiation in our Back Radiation post. It is distinct from the solar radiation that penetrates the atmospheric clouds because it is radiation emitted by the clouds, rain, snow, and atmospheric gas themselves.

In any cell, the long-wave radiation going up is the upwelling radiation and the long-wave radiation going down is the downwelling radiation. At the tropopause, the upwelling radiation is the heat leaving our planetary system. It is our total escaping power. When our simulation converges to equilibrium, we should find that the average solar power penetrating to the surface is equal to the average total escaping power.

Sinking Restored

When we added rain and snow to our Circulating Cells program, we removed the slow descent of microscopic water droplets, saying that their movement would be insignificant compared with that caused by convection. This is indeed the case when an equilibrium with plenty of atmospheric convection is established.

Nevertheless, we have found in our recent tests, in which we are allowing the clouds to radiate heat directly into space, that clouds can form and sit directly upon the surface, where they block the Sun's light. The surface cools beneath these clouds, and the clouds themselves cool by radiating into space, and we have seen them sit there fore hundreds of hours. This is unrealistic, because in a hundred hours, a cloud will sink by at least a few hundred meters.
So we restored the sinking of cloud droplets to our simulation, at 3 mm/s, which is realistic for cloud droplets 20 μm in diameter.

When we restored the sinking, we noticed that our previous implementation had allowed the clouds to sink only when the cells containing them took part in a convection circulation. As a result, the clouds were sinking through our simulated atmosphere a hundred times slower than they should have been. The fast-sinking implemented by CC9 were in fact sinking at 3 mm/s instead of 300 mm/s, and the slow-sinking clouds were sinking at only 0.03 mm/s instead of 3 mm/s. Thus our fast-sinking clouds were a more realistic simulation of the manner in which actual clouds would sink, while our slow-sinking clouds were unrealistically slow. We run our sinking cloud experiments with a corrected version of CC9, and the new slow-sinking result looked like the former fast-sinking result.

When clouds sink at 3 mm/s, they can sit on the surface for a few hours, but after a hundred hours, they disappear. The droplets will sink 1000 m in a hundred hours, which is three times the height of a gas cells resting upon the surface. The slow descent of the droplets removes clouds that would otherwise freeze the surface, and therefore plays an important role in our simulation, despite the fact that convection, rain, and snow cause movements that are thousands of times faster.