Equilibrium Point

Heat arrives at the Earth in the from of sunlight. The clouds reflect some of it. Almost all the rest arrives at the Earth's surface. Of the sunlight that reaches the surface, some is reflected back into space, especially by snow, but most is absorbed. To the first approximation, therefore, sunlight affects the climate only by it warming the surface, not by warming the atmosphere directly.

In our Circulating Cells simulation, version CC11, solar power is either reflected by clouds or absorbed by the surface. The only way for heat to enter the atmosphere is by contact with the surface, so it is the temperature of the surface that drives the the circulation of gases and the creation of clouds, snow, and rain. When we observe, for example, that 80% of solar power is penetrating to the surface when the surface gas temperature is 290 K, we can assume that the 80% of solar power will penetrate to the surface whenever the surface gas temperature is 290 K.

Our program of solar increase provides us with observations of cloud depth and penetrating power for a range of solar powers, and therefore for a range of surface temperatures. The following graph shows how the fraction of solar power penetrating to the surface varies with surface temperature.



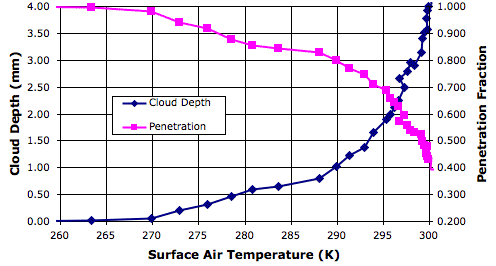
In our simulation we calculate the penetrating power for each surface block using the depth of the clouds in the column of cells above the surface block. We cannot, however, use the average cloud depth to obtain a measurement of average penetration fraction. When we do so, our measurement is always too low, because there are gaps in the cloud cover, and these gaps allow more light to pass through than if the clouds were distributed uniformly.

In the following graph, we have taken our measurements of penetration fraction and used them to calculate the power that would penetrate to the surface for two values of solar power: 350 W/m² and 400 W/m². Along with these penetrating powers, we also plot the total escaping power.



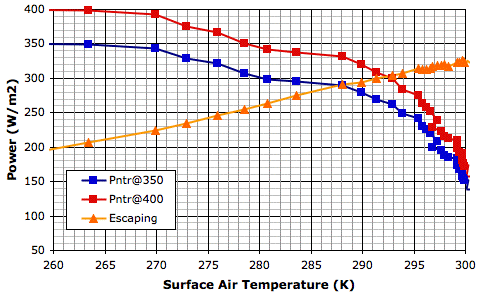
At thermal equilibrium, the total escaping power must be equal to the penetrating power. Thus the intersection of the penetrating power and escaping power graphs occurs at the equilibrium temperature. For solar power 350 W/m², the intersection occurs at 288 K. For 400 W/m², the intersection occurs at 292 K. These are, of course, the same equilibrium temperatures we obtain from our existing graph of surface temperature versus solar power.

In our next post, we will use the above graph and the calculations we presented in With 660 PPM CO2 to estimate how much the Earth would warm up if we doubled the CO2 concentration of its atmosphere.