One of our readers suggested we consider the atmosphere of Venus. What a good idea. Let's see how well we can estimate Venus's surface temperature using our understanding of atmospheric convection and the greenhouse effect.
According to Wikipedia, Venus's tropopause is at an altitude of 65 km with temperature 243 K (−30°C) and pressure 10 kPa. The surface pressure, meanwhile, is almost a thousand times greater: 9,300 kPa, which is ninety-three times the surface pressure on Earth. Venus's atmosphere is made up almost entirely of CO2, but also contains 150 ppm of SO2 (sulfur dioxide), and this SO2 condenses into liquid droplets so that the atmosphere below the tropopause is filled with pale yellow clouds.
Venus reflects 90% of incident sunlight (it's Bond Albedo is 0.90). The remaining 10% is absorbed. We're not sure what fraction of the Sun's light reaches the surface of Venus, but our guess is 1%. The SO2 clouds refract and reflect light like our own clouds, but SO2 is a pale yellow liquid, not a clear liquid, and will absorb sunlight eventually.
According to Schriver et al., even a 0.5-μm film of SO2 ice will absorb over 20% of long-wave radiation, so a 10-μm droplet of SO2 liquid will absorb it all. The clouds of Venus are near-perfect absorbers of long-wave radiation, and near-perfect radiators too, just like our own water clouds. Unlike the Earth, however, Venus is always entirely covered with clouds. Neither the planet surface nor the lower atmosphere has any opportunity to radiate heat directly into space. Venus radiates heat directly into space only from its cloud-tops and upper atmosphere.
Although most of the sun's heat is reflected back into space, 10% is absorbed, and we estimate that around 1% reaches the surface of the planet. This heat will raise the temperature of the surface until it forces convection. Here is the convection diagram from our Atmospheric Convection post.
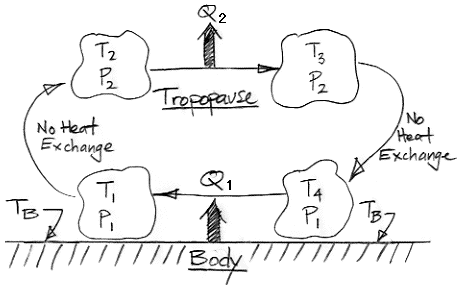
Gas warms at the surface. It rises, expands, radiates heat into space, falls, contracts, and warms again. As the gas expands, it gets cooler. As it contracts, it gets warmer. In our simplistic analysis, we assumed that the expansion and contraction were adiabatic, meaning they took place without any heat entering or leaving the gas. In reality, the gas radiates heat to nearby gas, absorbs heat from nearby gas, mixes with nearby gas, and generates heat through viscous friction. But our adiabatic assumption allowed us to estimate the temperature changes using the equation of adiabatic expansion and contraction. For an ideal diatomic gas, such as N2 or O2, p−0.4T1.4 remains constant during adiabatic changes, where p is pressure and T is temperature. For CO2, however, the equation is p−0.3T1.3 at 300 K and p−0.2T1.2 at 1300 K (see here for thermodynamic properties of CO2).
The Earth's tropopause is at altitude 15 km. According to our typical conditions, the tropopause is at 220 K with pressure 22 kPa, while the surface pressure is 100 kPa. Adiabatic compression implies that air descending from the tropopause to the surface will heat up to 340 K. But the Earth's surface is at only 280 K. Air descending 10 km from the tropopause to the surface appears to lose 20% of its heat while contracting to a third of its original volume.
The atmosphere of Venus will heat up as it descends from the tropopause to the surface, and it will be hottest if it does not lose any heat on the way down. The pressure rises from 10 kPa in the tropopause to 9,300 kPa at the surface. The temperature starts at 240 K. Adiabatic compression of an ideal diatomic gas would heat the gas to 1700 K. If we use p−0.25T1.25 as an approximation for CO2, we estimate a final temperature of 941 K.
According to Wikipedia, the surface temperature of Venus is actually 740 K. Carbon dioxide falling 65 km from the tropopause to the surface appears to lose 20% of its heat while being compressed into less than a hundredth of its original volume.
Despite the 20% difference between our calculations and our observations, we see that atmospheric convection makes the surface of Venus incredibly hot while leaving the surface of the Earth delightfully temperate.
If we recall our post on work by convection and another on atmospheric dissipation, we see that a strong convection cycle causes powerful weather. Venus's convection cycle produces an order of magnitude more contraction and expansion than the Earth's. We expect Venus's weather to be an order of magnitude more extreme. And indeed it is.

Hi Kevan,
ReplyDeleteHave you seen the discussions about Venus on www.scienceofdoom.com?
Convection, Venus, Thought Experiments and Tall Rooms Full of Gas – A Discussion
Posted in Atmospheric Physics, Basic Science on August 16, 2010 | 111 Comments »
During a discussion about Venus (Venusian Mysteries), Leonard Weinstein suggested a thought experiment that prompted a 2nd article of mine. Unfortunately, it really failed to address his point. In fact, it took me a long time to get to grips with Leonard’s point and 500 comments in (!) I suggested that we write a joint article. I [...]
Read Full Post »
Best wishes,
Hugh
So why is Venus so much cooler than expected? Is it convection?
ReplyDeleteWell, that depends upon what you mean by "expected".
ReplyDeleteSuppose we fill a cylinder with gas from Venus's tropopause. We compress it quickly until the pressure in the cylinder is almost a thousand times higher than it was to start with. The gas heats up inside the cylinder because its molecules are being thrown back off the contracting walls faster than they strike it. If the compression is fast enough, no heat will have time to escape the gas. The compression is adiabatic. The result is that the gas gets very much hotter. Indeed: it will get to 1700 K, having started at 240 K.
Suppose we perform the same compression, but we do it very slowly, so that any time the gas warms up, we let its warmth flow out of the cylinder and into the cold gas outside. Now the gas reaches its new pressure, and much smaller volume, but remains at the same temperature. The compression is isothermal.
When gas descends from the tropopause of Venus to its surface, it will be compressed by the weight of gas above. Will this compression be adiabatic or isothermal? It will be somewhere in-between. The heating of the gas during compression will be less than the heating we would obtain with adiabatic compression.
Thanks, Kevan. I have another question (in 2 parts). You introduce the following assumption: "We're not sure what fraction of the Sun's light reaches the surface of Venus, but our guess is 1%."
ReplyDelete(a) What are the grounds for making this assumption?
(b) How would it affect your subsequent argument if the fraction was 0%?
Dear Hugh,
ReplyDelete(a) My grounds for making this assumption are few. I know that the Venus probe that descended to the surface was able to view the surroundings for a few minutes in ambient light.
Now that you ask, however, I find that the surface illumination is comparable to Earth's on an overcast day, so my 1% estimate may be too low.
http://en.wikipedia.org/wiki/Sunlight
(b) If the fraction were 0%, there would be no convection from the surface. The 10% of sunlight that is not reflected would penetrate to some depth in the atmosphere. Convection would occur from this depth and upwards. The surface of the planet would be cooler because it is not being heated.
Yours, Kevan
Dear Hugh,
ReplyDeleteI really like your 0% question. Here's more in answer to it.
Let us suppose sunlight did not penetrate to the surface of Venus. Instead, the last of the sun's heat is absorbed at an altitude of 30 km where the pressure is 1,000 kPa. In that case, this heat must be transported from 10 km up to the tropopause at 65 km where the pressure is only 10 kPa. The gas at 10 km will be hotter than the tropopause. Convection will transport the heat up through the atmosphere. The more heat transported, the faster the gas must move and the more adiabatic the expansion and contraction will be, which we know means a larger temperature drop, which is consistent with the general principle of "more heat flow requires a larger temperature difference."
Below 10 km there is, by assumption, no heat arriving from the sun. There is no heat to transport away from the planet. There may be circulation of air, but this circulation will be slow, so that expansion and contraction of gas during circulation will be isothermal instead of adiabatic. There will be no temperature change as we descend from 10 km to the surface.
If we look at the temperature profile of Venus's atmosphere:
http://en.wikipedia.org/wiki/Atmosphere_of_Venus
we see that the temperature of the atmosphere rises all the way down, which means there is heat to transport from the surface. Much of this heat is carried up through 65 km of atmosphere by convection. Some of it is carried by radiation.
I think I should look into how much heat is transported by radiation as compared to convection.
Yours, Kevan
Kevan,
ReplyDeleteThanks again. The ambient light seems like a clincher for non-zero.
There must also be heat flow from the planetary interior. I doubt if it has been measured, tho.
Have you seen the discussions about Venus atmosphere at www.scienceofdoom.com?
"Venusian Mysteries – does the high pressure of the Venusian atmosphere (due to its huge mass) create the high surface temperatures?
Venusian Mysteries – Part Two – a more in-depth and technical look at Venus under certain artificial conditions"
I took a look at the scienceofdoom pages on Venus. I have already his arguments in the comments here
ReplyDeleteHe describes adiabatic compression, even saying that it has to occur quickly, and isothermal compression, saying that is must occur slowly. But then he goes on to say that any column of air will experience adiabatic circulation of gas, regardless of whether any heat is flowing in the bottom and out the top. He says that the air will circulate naturally without any heat input, expanding and contracting adiabatically, so as to maintain a temperature difference between the top and the bottom. He does not explain where the energy required by this rapid circulation of a viscous fluid will come from.
His belief defies the first law of thermodynamics: we cannot have viscous fluid circulating without a paddle to move it or heat flow to cause it.
Without heat going in at the bottom and out at the top, air circulation will be so slow as to be isothermal. The temperature of the column will be uniform. The pressure at the bottom will be greater because of the weight of the air above.
The author of scienceofdoom says, 'If you heat a gas sufficiently from the bottom, convection will naturally take place to redistribute heat. The environmental “lapse rate” can’t be sustained at more than the adiabatic lapse rate because convection will take over.'
Quite the opposite is true. Without convection, the column of air will be uniform in temperature. When we put heat in at the bottom and draw it out at the top, a temperature gradient develops. With enough heat flow, the temperature gradient approaches that of adiabatic expansion, because the heat transport occurs by convection.
If no heat entered Venus's atmosphere, it's temperature would be uniform. It is the heat of the sun, trapped by a thick atmosphere, that makes Venus so hot. Venus is an example of an extreme greenhouse.
Oh, and later on, another author on the same scienceofdoom page says of gas being poured into a tall column, "A dry adiabatic lapse rate forms as the gas is introduced due to the adiabatic compression of the gas at the lower level." What adiabatic compression is he talking about? If you pour gas into a cylinder, it will mix with the stuff below. There will be no adiabatic compression. If there is any compression as the gas builds up, it will lead to temporary vortices that will accelerate the mixing of the gas until the entire column is at a uniform temperature. Of course, trying to understand Venus when you hold this belief in magical adiabatic compression is indeed a challenging project, and we can see how challenging it becomes by the length of the three posts on the subject, and all the comments afterwards.
ReplyDeleteConsider this scieneofdoom statement again:
ReplyDeleteIf you heat a gas sufficiently from the bottom, convection will naturally take place to redistribute heat. The environmental “lapse rate” can’t be sustained at more than the adiabatic lapse rate because convection will take over.
The author is saying that the temperature difference from the bottom to the top of a column of gas is greatest when there is no heat flow. When we put heat in at the bottom and take it out of the top, the author is saying that the temperature difference from bottom to top will decrease.
Thus he argues that Venus would be hotter if there were not convection in its atmosphere, but by delivering heat to the planet surface, we start up convection, and the planet actually cools down
So: we heat it up and it cools down. With such a column of gas we can make a perpetual motion machine that violates the second law of thermodynamics.
I wonder if Venus ever cooled of? Or it might have a radioactive core like the earth and the thick atmosphere is holding the heat in.
ReplyDeleteI assume Venus has a radioactive core. Because only a small fraction of sunlight reaches Venus's surface, perhaps the heat from its radioactive core is significant compared to the incoming sunlight. Our calculation here is of the difference in temperature between the top and bottom of Venus's atmosphere. We add the increase due to compression to the measured temperature of the upper atmosphere to get the temperature at the surface. But we don't attempt to calculate the temperature of the upper atmosphere, which does the radiating into space. The heat the atmosphere must radiate will be the radioactive head plus the light energy that penetrates a significant distance down into the atmosphere.
ReplyDelete