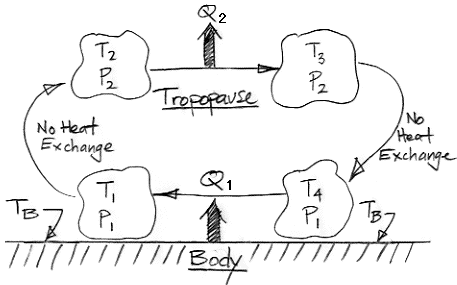
At Point 1, on the lower-left, the Volume has been warmed by contact with the Body. The Body itself, we recall, is being warmed by short-wave radiation from the Sun. This is an extreme greenhouse, so let's choose T1 = 400 K, TB = 405 K, and p1 = 100 kPa.
The Volume is now so warm that it is less dense than the lower-pressure air above. The Volume rises through the atmosphere. This atmosphere is black to long-wave radiation. The Volume emits and absorbs long-wave radiation, but it rises quickly enough that any imbalance in the radiation it emits and absorbs is negligible compared to the heat it absorbed from the Body. As the Volume rises, it mixes with other volumes of air at its borders. We assume the Volume is so large and rises so quickly that whatever happens at its borders is negligible compared to the vast bulk of the Volume within.
In short, we assume that any heat entering or leaving the Volume on the way up is negligible. The expansion of the Volume will be adiabatic. As a gas expands adiabatically, it cools down, even though no heat passes out of it. Given a particular pressure drop from adiabatic expansion in a particular gas, we can determine the corresponding change in temperature. Our Extreme Greenhouse atmosphere is mostly nitrogen and oxygen, both of which are diatomic molecules, and we have assumed our Volume is dry. In the adiabatic expansion of diatomic gases, p 0.4T −1.4 is constant, where p and T are the absolute pressure and absolute temperature of the gas respectively.
The Volume rises until it reaches the tropopause, which is Point 2 in the diagram. As we showed in an earlier post, the tropopause in our Extreme Greenhouse corresponds to the upper surface of the Filter Gas, and is at pressure p2 = 30 kPa. The Volume expanded adiabatically, so its temperature must now be T2 = 285 K.
At the tropopause, heat starts to leave the Volume. Heat leaves by radiation directly into space because there is too little atmosphere above the tropopause to absorb all the Volume's outward radiation. The Volume becomes more dense. It stops rising and it cools at constant pressure. At Point 3, the Volume has cooled until it is so dense that it starts to fall through the higher-pressure air below. Suppose it has cooled by 10 K so that T3 = 275 K.
Just as we assumed adiabatic expansion as the Volume rose, we now assume adiabatic compression as it falls. As the Volume descends to Point 4, its pressure increases from 30 kPa to 100 kPa, so its temperature must rise to T4 = 385 K. When it arrives at the surface, the Volume is once again in contact with the Body, which is at TB = 405 K. A typical value for the coefficient of heat transfer between a rough surface and moving air is 50 W/m2K. With this value, heat starts to flow from the Body to the Volume at 1000 W/m2. The Volume warms up. When it reaches T1 = 400 K, heat flows at 250 W/m2. At this temperature, however, the gas is light enough to rise. We have returned to Point 1 in our diagram, and the convection cycle begins again.
As we established in previous posts, the temperature of the tropopause in our Extreme Greenhouse depends only upon the amount of long-wave radiation it must emit into space, which is exactly equal to the amount of short-wave radiation absorbed by the Body from the Sun. In our Extreme Greenhouse, the tropopause must be at 280 K. In our convection cycle, the Volume cools from 285 K to 275 K in the tropopause. Its average temperature is 280 K. As its descends, it warms up by 115 K.
The atmosphere of our Extreme Greenhouse must transport 350 W/m2 from the Body to the tropopause, because this is the amount of heat the Body receives from the Sun. But we need less than a 10-K difference between the Volume and the Body to obtain this heat flow. This 10-K difference is small compared to the 115-K difference between the surface and the tropopause. We see that the temperature difference between the Body and the tropopause is dominated by the temperature difference required to drive convective cooling by adiabatic expansion. To the first approximation, the temperature difference between the Body and the tropopause does not depend upon the amount of heat that the atmosphere must transport. To the first approximation, the size of the greenhouse effect depends only upon the temperature of the tropopause and the ratio of the tropopause pressure to the surface pressure.
In our example, the tropopause pressure is 30% of the surface pressure so that the surface temperature must be 140% of the tropopause temperature. If the surface temperature were any lower, there would be no convective heat transport to the troposphere, and the Body would get hotter until convection started.
The pressure of the tropopause, meanwhile, depends upon the long-wave absorption spectrum of the atmosphere. In our Extreme Greenhouse, the atmosphere is black to all long-wave radiation because of a greenhouse gas mixed in with its nitrogen and oxygen. When we double the concentration of this greenhouse gas, the tropopause pressure drops from 30 kPa to 15 kPa. Its altitude rises from 12 km to 17.5 km. But the tropopause temperature must still be 280 K. After this doubling of concentration, the Body temperature must rise to 170% of 280 K, or 480 K. A doubling of greenhouse gas concentration raises the Body temperature by 75°C.

No comments:
Post a Comment