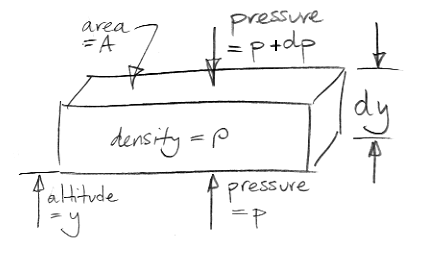
What holds up the weight of our element? The only external forces acting upon our element are pressure below and pressure above. We stop any argument about sheer forces at the edges by saying that all edge effects are negligible because dy is infinitely small. (That's our first use of the infinitesimal part of calculus.)
We assume our element is at rest with respect to the Earth. The pressure pushing up from below must be slightly greater than the pressure pushing down from above in order to hold up the weight of the element. Our drawing gives the pressure above as p+dp, where dp is a small difference in pressure. We will find that dp is negative. The upward pressure force is Ap. The downward pressure force is A(p+dp). For the vertical forces upon our element to balance we have,
Ap = A(p+dp) + ρAgdy
⇒ dp = −ρgdy
⇒ dp/dy = −ρg
The term on the bottom left is the "derivative of p with respect to y", or the "rate of change of pressure with altitude." We see that the derivative is independent of A, and is always negative.
We now introduce a further complication: the density of a gas depends upon pressure and temperature. According to Boyle's Law, p/ρT is constant, where T is absolute temperature. If we halve the pressure and keep the temperature constant, the density must also halve. We know that pressure drops to zero as we go up through the Earth's atmosphere. We also know that temperature drops from around 290 K at the surface to 210 K at the top of the troposphere. After that, the temperature rises again. If we assume temperature is constant at 250 K, we'll be right to ± 20%, which is good enough for our purposes, and simplifies our mathematics significantly.
Thus we assume there is a constant f such that f = p/ρ as we go up through the atmosphere. The density of air at atmospheric pressure and 250 K is roughly 1 kg/m3. Atmospheric pressure is 100 kPa (roughly ten tonnes per square meter). Thus f = 100 kPa / 1 kgm−3 = 105 Nm/kg, and for other pressures we have ρ = p/f. Our differential equation becomes,
dp/dy = −pg/f
The only relationship between p and y that satisfies our differential equation is the following, where we have p proportional to the natural number, e = 2.72, raised to a negative power in y.
p = p0e−gy/f
where p0 is the pressure when y = 0, which is 100 kPa. Gravity at the surface of the Earth is roughly 10 m/s2. The radius of the Earth is around 6,000 km, and gravity is proportional to the inverse square of distance, so gravity at the top of a 100-km thick atmosphere would be only 3% less. We can assume gravity is constant. Now we have,
p = 105 e−y/10 km Pa
Every 10-km increase in altitude causes the pressure to drop by 63%. At altitude 10 km, p = 37 kPa. At 20 km, p = 14 kPa. At 100 km, p = 0.005 kPa.
We will discuss our solution further in a later post. Until then, I invite you to consider the following questions. How is the weight of the atmosphere related to the pressure at sea-level? What altitude includes 99% of all atmospheric gas? If air was an incompressible fluid, so that ρ = 1 kg/m3 for all T and p, how deep would the atmosphere be?
UPDATE: For 1 kg of air we have p/ρT = R, where R is the specific gas constant for air and is equal to 287 J/kgK. Thus f = RT, and our equation for pressure with altitude becomes p = p0e−gy/RT. The altitude at which the pressure drops by 63% is a function only of temperature, a fact that emerges in the comments of Adiabatic Balloons.
UPDATE: Because most of the mass of the atmosphere is below 10 km, we should bias our average temperature more towards the surface temperature. Let us use 260 K for the average air temperature on a warm day. Using 287 J/kgK for R, we estimate the pressure will drop by 63% in 6.5 km instead of 10 km, which is consistent with typical conditions in our atmosphere.

No comments:
Post a Comment