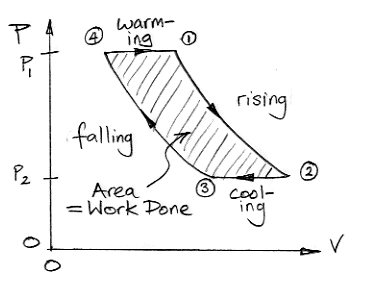
From (4) to (1) the gas warms at constant pressure while in contact with the Body. From (1) to (2) it rises through the atmosphere, expands, and cools. From (2) to (3) it cools at constant pressure in the troposphere by radiating its heat into space. From (3) to (4) it descends, contracts, and warms.
A pressure-volume plot allows us to determine the amount of work done by the air taking part in our cycle. Consider a volume of air, v, at pressure p in a cylinder with a piston. The piston has cross-section A. We let the air expand a small amount dv. The work done by the gas is equal to the force on the piston, pA, multiplied by the distance the piston moves, dv/A. So the work done is pdv. This relation holds regardless of the shape of the gas volume as it expands by dv at pressure p. The work done is equal to the integral of pressure with respect to volume, which is the area under the plot of pressure versus volume.
The area under the plot from (4) to (2) is the work done by the gas as it expands. The gas does work compressing the surrounding atmosphere. The area under the plot from (2) to (4) is the work done upon the gas as it contracts. The surrounding atmosphere does work to compress the gas. The amount of work done by the warm, expanding gas is greater than the amount of work required to compress the cool gas. The area enclosed by the pressure-volume plot is positive. Not only does the convection cycle transport heat up through the atmosphere, it also does work.
We could place windmills or turbines in the way of the air that rises and falls in our convection cycle, and so extract work from the cycle. Where does the energy for this work come from? There are no windmills or turbines in the way of the air in our extreme greenhouse, so what happens to the work produced by the convection cycle?
We will try to answer these questions in our next post on the subject.

No comments:
Post a Comment