The absorption spectrum of water vapor is not so simple. We have already presented our readers with the absorption spectrum of liquid water. But we cannot simply divide this spectrum by the fraction of water present in air and so obtain the spectrum for water vapor. Water vapor is water dissolved in air. The spectrum of liquid water applies to the Earth's oceans, and to the tiny droplets of water in clouds, but it does not apply to water vapor, as we saw in Vapor Versus Liquid. Water vapor absorbs several orders of magnitude less long-wave radiation than we would expect from dividing the liquid water spectrum by the water vapor concentration.
In liquid water, there are hydrogen bonds between each water molecule and its neighbors. These bonds absorb long-wave radiation. Hydrogen bonds are far less common in water vapor because the molecules are separated. Hydrogen bonds occur in water vapor when pairs of molecules join together to form dimers. The hydrogen bonds in these dimers absorb long-wave radiation. The chance of a water molecule finding a partner to form a dimer increases with concentration. At the same time, the number of water molecules per unit volume increases with concentration. The result is that the absorbing power of water vapor increases as the square of the concentration. Absorption by water vapor is also temperature-dependent because dimers are broken apart by kinetic energy, so colder dimers live longer and have more opportunity to absorb long-wave radiation.
There are also weak long-wave absorbing bonds between water and nitrogen, and water and oxygen. The absorption of long-wave radiation by water vapor is an on-going subject of research at many institutes. The relationship between molecules in water vapor is called the water vapor continuum. In Water vapor absorption coefficients in the 8−13-μm spectral region: a critical review (1990), Grant et al review existing measurements of the water vapor continuum spectrum. In Recent Developments in the Water Vapor Continuum (1999), Mlawer et al review existing calculations of the spectrum. The following graph of water vapor continuum absorption agrees well with measurements such as these.
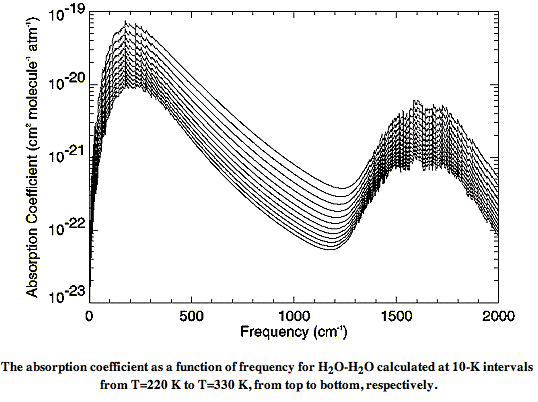
Instead of plotting the spectrum versus wavelength, this graph plots the spectrum versus the inverse of the wavelength, in units of cm−1. The spectrum itself takes the form of a quantity in units of cm2 molecule−1 atm−1, plotted for various temperatures between 220 K and 330 K. In our next post, we will convert this graph into one of absorption length versus wavelength, and show how we can calculate the absorption of long-wave radiation by water vapor in the atmosphere.
PS. Thanks to Peter Newnam for his help researching this post.
UPDATE: See CO2 Continuum for the spectrum of diluted CO2.