Planetary Greenhouse, Part Two

We continue our Planetary Greenhouse discussion. The atmosphere around our imaginary planet contains nitrogen and oxygen, which we choose because these diatomic gases are transparent to both short-wave and long-wave radiation. But the atmosphere also contains an imaginary greenhouse gas that is transparent to wavelengths shorter than λ_T, but absorbs longer wavelengths with constant absorption length, L_T.

We wrote a computer program to determine the total heat radiated per square meter by the planet and its atmosphere. Before we can run the program, we must choose λ_T and L_T.

Consider the absorption spectrum of pure CO2 at roughly 300 K and 100 kPa, which we present here. Between 8 μm and 11 μm the gas is transparent. The graph of radiated power versus wavelength for a black body at 300 K, which we present here, shows a peak at around 10 μm, right in the middle of CO2's transparent band. Meanwhile, the gas is at its most opaque for wavelengths greater than 13 μm. The absorption length drops to as little as 1 cm between 13μm and 17 μm, but is close to 1 m for 17 μm and higher. Let us choose λ_T = 13 μm and L_T = 1 m.

Suppose our greenhouse gas makes up 330 ppm by volume of the atmosphere around our imaginary planet. Suppose the pressure at the planet surface is 100 kPa and the temperature is in the neighborhood of 300 K. The absorption length of the atmosphere at at the surface will be 1 m / 330 ppm = 3 km for wavelengths greater than λ_T. In The Upper Gas we showed how the absorption length at the surface is related to the pressure in the tropopause. With absorption length 3 km at the surface, the tropopause pressure will be 30% of the pressure at the surface, or 30 kPa. If we double the concentration of the greenhouse gas from 330 ppm to 660 ppm, the absorption length at the surface decreases to 1.5 km, and our tropopause must rise to an altitude where the pressure is only 15 kPa.

Now we can run our program, and we do so. We calculate the sum of the power radiated directly into space by the planet surface and by the troposphere. We plot this total radiated power versus the temperature of the planet surface, and we do so for a range of tropopause pressures.



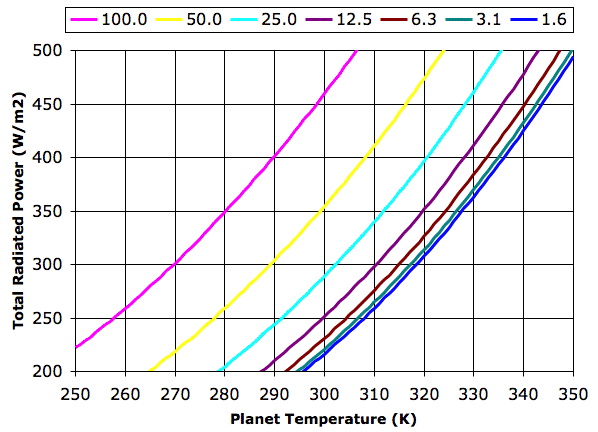
The graph legend gives tropopause pressure in kPa. Each halving of pressure corresponds to a doubling in greenhouse gas concentration. The 100 kPa graph represents the case where the concentration is so low that the troposphere is at the planet surface. The planet radiates like a black body directly into space. The 1.6 kPa graph represents a concentration so high that the the troposphere radiates hardly any heat into space. The atmosphere acts to block all radiation at wavelengths greater than λ_T.

For thermal equilibrium in our Planetary Greenhouse, the total power radiated into space, E_P + E_T, must be equal to the total power received from the sun, E_S. In Solar Heat we showed how the average power reaching the Earth from the Sun was 350 W/m², and we calculated that the surface of a black planet with no atmosphere would be 280 K. In the 100 kPa graph above, we see that the surface temperature, T_P, crosses 280 K when the total radiated power is 350 W/m².

Let us suppose that the total radiated power in our Planetary Greenhouse must be 350 W/m². With a tropopause pressure of 50 kPa, the planet surface must be at 299 K. If we double the concentration of our greenhouse gas, the planet warms by 13 K. Subsequent doublings in concentration raise the temperature by an additional 7 K, 5 K, 3K, and 1 K.