Extreme Greenhouse, Part Three

The diagram below shows a body heated by short-wave radiation, E_S. The Body is covered by three layers of gas. The Lower and Upper Gas are transparent to both short-wave and long-wave radiation. The Filter Gas is transparent to short-wave radiation but black to long-wave radiation. In later posts, we will see how a layer of transparent gas below a layer of black gas can be used to model the gradual absorption of long-wave radiation in the Earth's atmosphere. As before, we assume our system is in thermal equilibrium, which means that all temperatures are constant. No part of the system is heating up or cooling down.



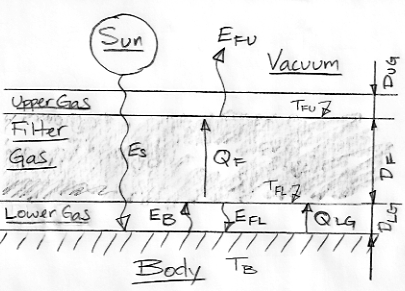
By radiative symmetry, the Upper Gas radiates no heat. Nor can it transport heat into the vacuum by convection or conduction. The temperature of the Upper Gas is constant, so it cannot be gaining or losing heat. It must be at the same temperature as the upper surface of the Filter Gas, which is T_FU.

Thermal equilibrium for the entire system dictates that Q_F = E_FU = E_S. In our previous post we assumed E_S = 350 W/m² for similarity with the Sun and the Earth, and we showed how Stefan's Law dictates that T_FU = 280 K.

We also assumed Q_F = K_F(T_FL−T_FU) and we chose K_F = 4.4 W/m²K. But this equation for Q_F says nothing about the depth of the filter. Let us now relate the heat flowing through each gas layer to its depth with a single coefficient, k, with units of W/mK.

Q_F = k(T_FL−T_FU)/D_F, Q_LG = k(T_B−T_FL)/D_LG

For k, let's choose 350 W/m² / 80 K × 10 km = 44 kW/mK. We choose 80 K because that's roughly the drop across the Earth's troposphere, and we choose 10 km because that's roughly the altitude of the Earth's tropopause. With D_F = 10 km and Q_F = 350 W/m² we have T_FL−T_FU = 80 K, so that T_FL = 360 K.

Let us consider thermal equilibrium at The Body surface. We must have E_S + E_FL = E_B + Q_LG. We apply Stefan's Law to obtain the following.

E_S + σ(T_FL)⁴ = σ(T_B)⁴ + k(T_B−T_FL)/D_LG

Where σ = 5.7×10⁻⁸ W/m²K⁴ and k = 44 kW/mK. Suppose we assume D_LG = 1 km. We have already calculated that T_FL = 360 K, so we arrive at the following relation for T_B.

(T_B)⁴.(5.7×10⁻⁸ W/m²K⁴) + T_B.(44 W/m²K) = 17 kW/m²

The solution to this equation is T_B = 366.4 K = 94.5°C. With a vacuum in place of the Lower Gas, we found T_B = 390 K = 117°C. Thus the addition of the Lower Gas reduced the temperature of The Body by 24°C. At this temperature, E_B = 1.03 kW/m² and E_FL = 960 W/m², so that The Body is radiating 70 W/m² more heat to the Filter Gas than the Filter Gas is radiating back to The Body. But Q_LG = 280 W/m². Convection accounts for 80% of the net 350 W/m² passing from The Body to the Filter Gas. Imbalance in radiative transfer accounts for only 20%.

In future posts, we will see how our three-layer gas model can be used to approximate heat transfer through the Earth's atmosphere, and allow us to estimate the influence of carbon dioxide concentration upon the Earth's temperature.