Continuum Absorption Length

Our job today is to convert this graph of water vapor continuum absorption coefficient versus frequency into a graph of absorption length versus wavelength. The original graph does not give absorption coefficient directly. Instead, it gives the absorption coefficient (in inverse centimeters) divided by the density of the water vapor (in molecules per cubic centimeter) divided by the water vapor partial pressure (in atmospheres). There are twelve plots in the graph, each representing the continuum absorption at a different temperature. We zoomed in on the graph and used a cross-hair cursor to translate several of the curves into numbers. You will find our numbers in the Water Vapor page of our Climate Spreadsheet here. We plotted absorption length for three combinations of water vapor concentration (in percent of volume), vapor pressure (in millibar), and temperature (in Kelvin). We superimposed the radiation spectrum of a black body at 300 K so that we can estimate the fraction of radiated power that will be absorbed by the first few kilometers of the Earth's atmosphere.



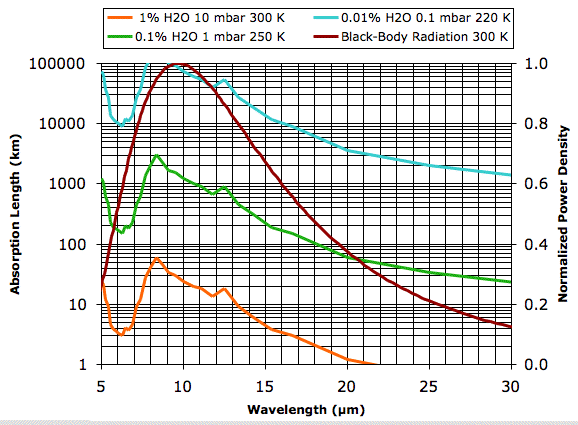
Plots of water vapor concentration versus altitude, such as this one for the Earth's atmosphere, show the concentration varying from as much as 4 % at sea-level to less than 0.0001 % at 10 km. Our plot of 1% water vapor at 10 mbar and 300 K is typical of the first 1 km of the atmosphere for 20° to 40° latitude on Earth. The absorption length of the water vapor continuum under these conditions is greater than 3 km for all wavelengths less than 16 μm. But for wavelengths greater than 20 μm the absorption length drops below 1 km. Looking at the graph, we estimate that 90% of the heat radiated straight up by the Earth's surface in these latitudes at wavelengths greater than 16 μm will be absorbed by water vapor before it reaches outer space.

Heat is radiated in all directions, which means most of it must pass through the atmosphere obliquely. Meanwhile, the atmosphere at the poles is dry, while the atmosphere in the tropics is humid. But the tropics are hotter than the poles, so that they radiate twice as much heat per square meter, and they cover a larger area too, so they contribute more to the total heat radiated by the Earth's surface.

Our guess is that almost all the heat radiated by the Earth's surface at wavelengths greater than 16 μm is absorbed by water vapor before it can reach outer space. These wavelengths represent roughly 30% of the total heat radiated by the Earth's surface.

PS. We spent several hours comparing our graphs with other calculations and measurements of water vapor absorption we found on the Internet. We believe we found good agreement between these calculations and measurements, although this agreement was not always obvious. For example, this graph from this report plots the absorption coefficient in cm²molecule⁻¹, without mentioning the partial pressure. But we believe the graph corresponds to a partial pressure of 1 mbar. At 10.6 μm, the graph says 1.8 ×10⁻²⁵ cm²molecule⁻¹, while Cormier et al measured 1.82 ×10⁻²² cm²molecule⁻¹atm⁻¹ at the same wavelength. One atmosphere is almost exactly a thousand millibar.

PPS. So far as we can tell from sites like this one, absorption of long-wave radiation by the water vapor continuum is absorption by bonds between water vapor molecules, but does not include absorption by the bonds within the water molecules. Absorption within water molecules takes place at specific frequencies, so that a plot of absorption length versus wavelength contains valleys so sharp they appear only as lines. The line at 1.1 μm, for example, is only 0.00002 μm wide (see Figure 3 here). With one such line every 0.02 μm, the lines would absorb only 0.1% of the radiation emitted by a planet surface. But such lines have a tendency to get broader when the water vapor molecules are colliding with other gas molecules, and this broadening greatly increases the fraction of long-wave radiation these lines absorb. Thus, absorption by the water vapor continuum represents some, but not all, of the absorption by water vapor.

PPPS. This history of infra-red astronomy shows that we have to get up above 3 km in a dry part of the world in order to see infra-red light from outer space. Even then, we can see only wavelengths that neither water vapor nor CO2 will absorb, and the seeing is good only when we are looking straight up. See our Vapor Versus Liquid post and its ensuing comments for more details.