When we wrote the first draft of this post, every explanation for the greenhouse effect that we had found on the web contradicted either the
second law of thermodynamics, or the laws of
black body radiation, or our own
laboratory experiments. At first we thought these contradictions meant that the greenhouse effect did not exist, and we were
not alone in coming to this conclusion. Our initial title for this post was "Refutation of the Greenhouse Effect". But we were mistaken. The greenhouse effect is a simple phenomenon that occurs when we have the correct planetary surface and atmosphere.
The
greenhouse effect is the "heating of the surface of a planet or moon due to the presence of an atmosphere containing gases that absorb and emit infrared radiation." In the context of the theory, these gases are called
greenhouse gases. In the case of Earth's atmosphere, the greenhouse gases include water vapor, carbon dioxide, and methane. As we described in
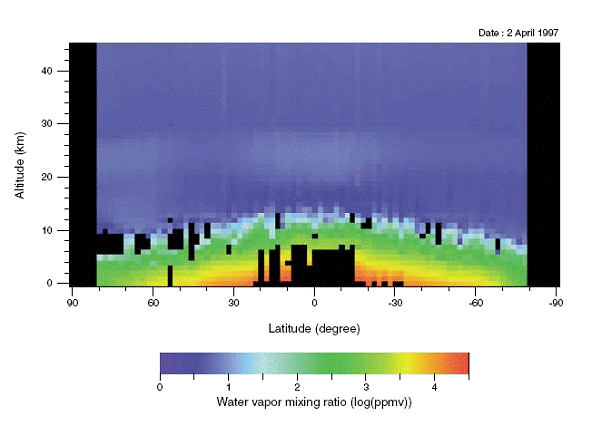
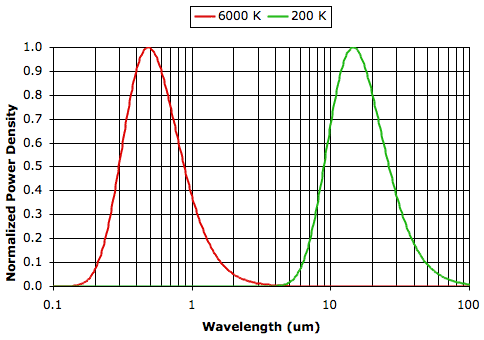
A Radiation Experiment, most of the heat arriving from the Sun is of wavelength less than 2 μm, while most of the radiation emitted by the Earth is of wavelength greater than 2 μm. Greenhouse gases, water vapor
in particular, absorb a small fraction of the radiation arriving from the Sun, but a large fraction of the radiation emitted by the Earth.
Suppose the atmosphere consisted only of nitrogen, oxygen, and argon. These gases are transparent to both the Sun's and the Earth's radiation. As we showed in
Radiative Symmetry, transparent gas cannot radiate heat. So an atmosphere of nitrogen, oxygen, and argon would not radiate heat. There would be no radiation of heat into space by the upper atmosphere. Without such radiation, the atmosphere would be calm and still, and its
temperature uniform.
Suppose we now add greenhouse gases to the atmosphere. These gases provide a means for the atmosphere to radiate into space the heat it acquires from the surface of the Earth. Convection is the
dominant source of atmospheric heating near the Earth's surface. But radiation is a significant source of heat transfer between layers of the atmosphere. The Second Law of Thermodynamics
dictates that all gases are exactly as effective at radiating heat as they are at absorbing heat. The Second Law
further dictates that no gas can distinguish between the heat it acquired by absorption of radiation and the heat it acquired by convection. Because of greenhouse gases, a packet of air in the upper atmosphere radiates heat into space. It cools. As it cools, it becomes more dense. It sinks back to Earth. A new packet of warm air rises to take its place. As air rises, it expands and cools, but it is the cooling by radiation at the top of the atmosphere
that drives the circulation of air between the lower and upper atmosphere. This radiating atmosphere is turbulent and cooler at the top than the bottom.
Suppose we warm a brass disk with an incandescent lamp and cover the disk with a film of water that cannot evaporate. Does the water film cause the disk to warm up or cool down? In
A Radiation Experiment and
The Cling-Film Diaper we showed that the disk cools down. It cools down because the water film is a far more effective infrared radiator than brass. Water vapor is also an effective radiator of infrared, and there is plenty of water vapor in the Earth's atmosphere. If the Earth were made of brass, water vapor in the atmosphere would allow the Earth to radiate heat more effectively, and so would act to lower the temperature of the Earth, not warm it up. But the Earth is not made of brass. Two thirds of it is covered with water. Unlike brass, the oceans are excellent radiators of heat.
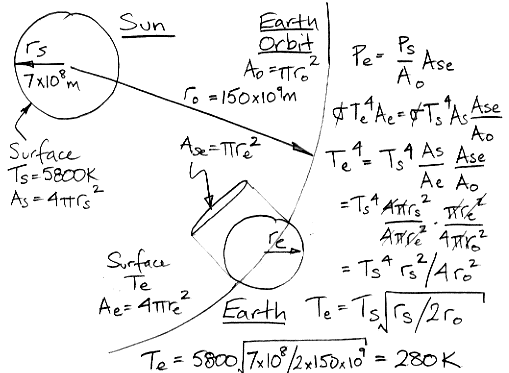
Consider a planet, such as the Earth, that is covered for the most part with oceans and yet somehow, for the sake of argument, has an atmosphere that is transparent to both the sun's and the ocean's radiation (that is to say, the atmosphere contains no water vapor, despite being covered with water). The ocean will warm up in the light of the sun until it reaches a certain temperature,
Tt. The atmosphere will warm up to the same temperature through its contact with the ocean. At this temperature, the ocean is radiating as much heat as it receives from the sun. The atmosphere, being transparent, radiates no heat. The upper regions of the atmosphere do not radiate heat. They do not cool down. The atmosphere's temperature is uniformly
Tt, and the atmosphere is calm.
We now add water vapor to the atmosphere, which will occur naturally through evaporation from the oceans, provided
Tt is high enough. And let us assume, again for the sake of argument, that there are no clouds formed from this water vapor, even though this is an unrealistic assumption. The water vapor makes the atmosphere opaque to radiation from the ocean, but the atmosphere remains transparent to radiation from the sun. The radiating surface of the planet is no longer the ocean, but the upper reaches its humid atmosphere. It is the upper atmosphere that must be at temperature
Tt in order to radiate heat at the same rate that the ocean is absorbing heat from the sun. Of course, the upper atmosphere was already at
Tt before we added the water vapor, so its temperature does not change. Now we must consider how the heat that the ocean absorbs from the sun will get to the upper atmosphere, where it can be radiated into space. According to the Second Law of Thermodynamics, the ocean will have to be warmer than the upper atmosphere in order for heat to flow to the upper atmosphere. Thus the ocean warms up to some new temperature
Tg >
Tt, and it is this warming that is called The Greenhouse Effect.
UPDATE [01-JAN-16] Of course, it is unrealistic to suppose that any atmosphere containing water vapor, and radiating heat into space, will contain no clouds. The warm air rising from the surface of the Earth expands as it rises, because its pressure drops. As it expands, it
cools down. As it cools down, its water vapor
condense into clouds. A
thick cloud can reflect 90% of the sun's radiation. If the Earth were to be covered by thick clouds, its surface would cool dramatically. We
calculate it would cool by almost 100°C. But if the Earth cooled by 100°C, there would be very little evaporation from the frozen oceans, and therefore insufficient water vapor in the atmosphere to cover the planet with thick clouds. We see that the Earth cannot be too warm, for it would then be covered by clouds and it would cool down, nor can it be too cold, for it would then have a clear sky and warm up. The result is that the Earth's surface settles to temperature at which cooling by clouds is in equilibrium with warming by the sun and by the greenhouse effect. We explore this
equilibrium with calculations and simulations in our later posts.