Extended Atmospheric Absorption Spectra

In our previous post we concluded that we needed to extend our existing absorption spectra to cover the range 5 μm to 60 μm. So we returned to the Spectral Calculator and, entered our gas properties for each atmospheric layer, and obtained the absorption spectra from 30 μm to 60 μm. We added these to our existing spectra and obtained the following graph (click for a larger version).



As a point of detail, each spectrum we receive from the Spectral Calculator contain tens of thousands of values. We condense the spectra using a program that calculates the average absorption in each 0.1-μm window. The result is a spectrum with a point every tenth of a micron. You will find the original spectra in our data archive, in the EA_1 folder. You will find the condensed spectra here. The condensed file can act as input to our climate models and is convenient for generating plots like the one above.

We apply our total escaping power program to our extended spectra and obtain the following values for power per square meter. For an explanation of the various columns, see here.

------------------------------------------------
      Name    Temp       BB     Layer   Escaping
------------------------------------------------
   Surface    290.0    401.1    388.8     89.8
      0-km    280.0    348.5    262.6     58.9
      3-km    270.0    301.3    184.8     49.7
      6-km    250.0    221.5    111.5     51.4
      9-km    230.0    158.7     50.7     29.4
     12-km    220.0    132.8     22.2     11.2
     15-km    220.0    132.8     14.4      5.5
------------------------------------------------
Total:                                   296.0
------------------------------------------------

Let's look at the first line of numbers, which apply to the surface of the Earth. We treat the surface as a black body, as we justify elsewhere. Using Stefan's Law we find that a black body at 290 K (that's 17°C) should radiate 401.1 W/m². Our calculator adds the power radiated in each 0.1-μm window from 5 μm to 60 μm, in a process we call numerical integration, and arrives at 388.8 W/m². That's closer to 401.1 W/m² than the 349.0 W/m² we obtained when we our calculation extended only to 30 μm. But we still have a difference of 12.3 W/m².

We experiment with the black-body radiation spectrum using this program. When we integrate in 0.1-μm steps all the way from 1 μm to 300 μm, we get a total power of 401.0 W/m², which is almost exactly what we obtain from Stefan's Law. We use our program to determine the power radiated by a black body at various wavelengths.

--------------------------
Range (um)  Power (W/m^2)
--------------------------
0.1-1          0.0
1-5            3.8
5-60         388.8
60-100         6.4
100-200        1.8
200-300        0.2
--------------------------
Total        401.0
--------------------------

We have a total of 12.2 W outside the 5-60 μm range of our absorption spectra. In the future, perhaps we will extend our spectra to include this missing 3%, but for now we are content with our omission. Furthermore, we are satisfied that our numerical integration in 0.1-μm steps, which is the basis of our climate model's calculations, is accurate to better than 0.1%.

Our next step is to generate a new set of spectra for the atmosphere with 660 ppm CO2, and see how the total escaping power changes. Our guess is that the total escaping power will decrease, but we are not sure by how much.

Total Escaping Power

Our current approach to modeling the Earth's greenhouse effect is to divide the Earth's atmosphere in to 3-km layers. So far, we have considered how each of the first seven layers absorbs and emits long-wave radiation. Our study of these seven layers has been motivated by a desire to calculate the total heat radiated into space by the Earth and its atmosphere, and ultimately to estimate the strength of the relationship between the Earth's surface temperature and the concentration of CO2 in its atmosphere.

In previous posts, we simplified our discussion by assuming that each atmospheric layer was either perfectly transparent or absolutely opaque at each wavelength. This assumption, combined with an examination of the absorption spectra, allowed us to say that all radiation passing through one layer would be sure to pass through all higher layers as well. Furthermore, our assumption allowed us to ignore the fact that most upward radiation is not vertical, but at some angle to the vertical. Radiation traveling at 60° to the vertical will pass through 6 km of air as it ascends through a 3-km layer, and so is more likely to be absorbed by the layer. But if we assume that the 3-km layer is either perfectly transparent or absolutely opaque, we conclude that radiation of a particular wavelength will either pass entirely through the layer or be entirely absorbed by the layer, regardless of its direction of travel.

Today we present our first layered-atmosphere computer model. The model does not assume that each layer is either transparent or opaque. When we calculate the power escaping into space from layer A at temperature T between wavelengths 10.0 μm and 10.1 μm, we proceed as follows. We start with the black-body radiation power density at wavelength 10 μm and temperature T. This power density is almost constant in the narrow range 10.0 μm to 10.1 μm, so we multiply the power density at 10.0 μm by 0.1 μm and obtain a good estimate of the power radiated between 10.0 μm and 10.1 μm. Now we multiply this power by the fractional absorption of layer A at 10.0 μm. The principle of radiative symmetry dictates that the efficiency with which a body emits radiation at a particular wavelength, as a fraction of the power emitted by a black body, is exactly equal to the efficiency with which it absorbs that same wavelength. So we now have the power radiated by layer A between wavelengths 10.0 μm and 10.1 μm. By assumption, whatever is not absorbed by the layer above A will escape into space, so we multiply the power radiated by A by the fractional transmission at 10.0 μm (that's one minus the fractional absorption at 10.0 μm) of the layer immediately above, and so arrive at the power between 10.0-10.1 μm that escapes from layer A into space.

To obtain the total power escaping into space from each layer, we add up the power escaping in all the 0.1-μm bands from 5 μm to 30 μm, which is the extent of our absorption spectra. We will include the surface of the Earth as its own layer. As we have in the past, we will assume the Earth's surface is a black-body radiator. Thus our program will calculate for us the total power escaping from the Earth into space, and allow us to see how much of this power is radiated by the surface and by each atmospheric layer.

Although we have dropped the transparent-opaque simplification, we retain two of its corollaries. First, we ignore the fact that most upward radiation is not vertical. Second, we assume that any radiation that manages to pass through the layer immediately above will be sure to pass through all remaining layers. These assumptions will effect our estimates, but we believe the effect will be less than 10%. In the future we may enhance our model to remove these assumptions, but for now we will start with a simple model.

We wrote our computer model in TclTk. You will find it here. The program takes as its input this file containing the names of the layers, their temperatures, and their absorption spectra. It produces the following output.

------------------------------------------------
      Name    Temp       BB     Layer   Escaping
------------------------------------------------
   Surface    290.0    401.1    349.0     89.7
      0-km    280.0    348.5    225.3     58.8
      3-km    270.0    301.3    150.0     49.8
      6-km    250.0    221.5     81.5     44.4
      9-km    230.0    158.7     31.2     15.4
     12-km    220.0    132.8     16.3      5.8
     15-km    220.0    132.8     13.1      4.2
------------------------------------------------
Total:                                   268.2
------------------------------------------------

The "Layer" column is the power radiated upwards by each square meter between 5 μm and 30 μm. The "Escaping" column is the power that escapes. We used 290 K for the surface temperature, which is 17°C. The total power escaping into space is 268 W/m². We don't have radiation from the 18-km layer, because we use this layer only as an absorber for radiation from the 15-km layer. The atmosphere above 15 km plays little or no part in atmospheric convection because it is above the tropopause.

We see immediately that the power escaping from the 15-km layer is only 1.5% of the total escaping power, and twenty times less than the power escaping from the Earth's surface. The top three layers of the atmosphere combined contribute less than 10% to the total escaping power. These are the layers in which radiation is dominated by CO2. In the lower layers, radiation is dominated by water vapor.

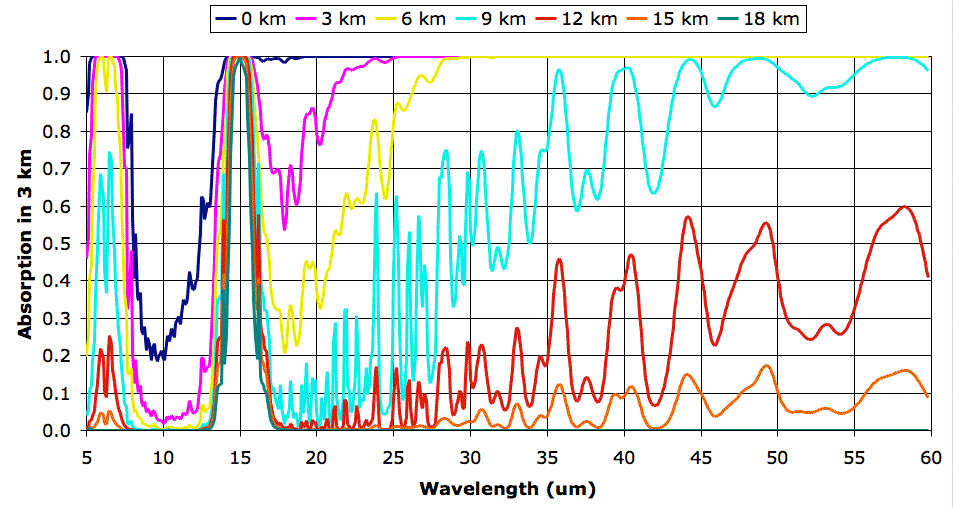
Before we proceed with exercising our model, however, we must correct a deficiency in our existing spectra. Our spectra extend from 5 μm to 30 μm, but it turns out that a significant portion of the heat radiated by the Earth's atmospheric layers is radiated in the range 30 μm to 60 μm, as you can see in the graph below. (In case you are interested, we obtained the curves of this graph using this program.)



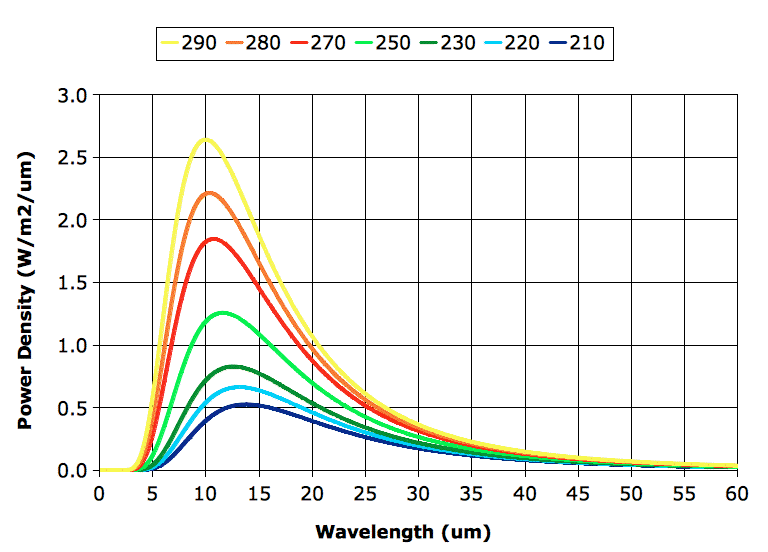
The "BB" column in our table gives the power a black body would radiate, as calculated using Stefan's Law. Our calculation assumes the Earth's surface is a black body, so when we see 401 W/m² in the "BB" column, we expect to see the same value in the "Layer" column. But we don't, and the reason we don't is because our calculation adds up only the power radiated by each layer in the range 5 μm to 30 μm. A black body at 290 K radiates only 349 W/m² in this range. The remaining 52 W/m² it radiates in the range 30 μm to 60 μm.

We must go back to the Spectral Calculator and extend our spectra to 60 μm. While we are there, we will obtain the spectra for 660 ppm CO2 and 165 ppm CO2 as well.

CO2 Absorption Band

In our previous post, we presented this graph of absorption by the Earth's atmosphere between 18 km and 21 km. This absorption is due entirely to CO2. In our calculations we set water vapor concentration to zero. Indeed, the absorption in the range 13-17 μm is due almost entirely to CO2 starting at an altitude of 9 km. The following plot gives us a close-up of the CO2 absorption in 3-km layers.



The four graphs are for 9, 12, 15, and 18 km, but we have named them after their atmospheric pressures, 410, 300, 220, and 160 mbar respectively. These pressures do not, in fact, correspond exactly to the pressures we observe in the atmosphere, because our pressure calculation ignores the drop in temperature as we ascend, but we used these pressure values when we calculated the spectra.

What we see between the absorption at 160 mbar and 300 mbar is the effect of doubling the density of CO2 molecules. In both cases, CO2 concentration is 330 ppm, which means 330 out of every 1,000,000 molecules are CO2. But the number of molecules per cubic meter increases approximately with the pressure, so the 300-mbar plot represents twice as much CO2 per cubic meter as the 160-mbar plot.

The absorption at 160 mbar for wavelength 14 μm is 21%, rising to 99% at 15 μm. The absorption at 300 mbar for wavelength 14 μm is 42%, rising to 99% at 15 μm. Twice as much CO2 in a 3-km layer leads to twice as much absorption of 14-μm radiation, but no significant increase in absorption of 15-μm radiation. We are particularly interested in the effect of doubling CO2 concentration, so let us try to get a better idea of how much more absorbing power the atmosphere has at 300 mbar than 160 mbar. Suppose a lower layer of the atmosphere emits uniformly in the band 13-17 μm, so that there is equal power in each 0.5-μm division of our graph. We can count squares under each graph and divide by the total number of squares to get the fraction of power absorbed by CO2 at each pressure. We come up with 43% at 160 mbar and 56% at 300 mbar.

Of course, the lower layers of the atmosphere do not radiate uniformly in the 13-17 μm band. Their radiation in this band is dominated by their own CO2, in accordance with radiative symmetry. The 300-mbar layer will receive radiation from the 410-mbar layer below it, and this radiation will have a power distribution that matches the 410-mbar layer's own absorption spectrum. At 14 μm, for example, the 410-mbar layer will radiate only 60% as much power as it does at 15 μm. In our spreadsheet we multiply the radiation spectrum of the 410-mbar layer by the absorption spectrum of the 300-mbar layer, and find that the 300-mbar layer absorbs 74% of the radiation arriving from the 410-mbar layer below. Meanwhile, the 160-mbar layer absorbs 70% of radiation from the 220-mbar layer below it.

The greenhouse effect causes a convection cycle in the Earth's atmosphere, which transports heat from the Earth's surface to the tropopause. All layers of the Earth's atmosphere up to the tropopause radiate heat out into space through the thinner, upper layers. As our previous posts have shown, radiation by the lower layers is dominated by water vapor, while radiation by the upper layers is dominated by CO2. Our calculations suggest that doubling the atmosphere's CO2 concentration will cause only a slight increase in the absorption and emission of radiation by the upper layers. In future posts, we will try to estimate how much this slight increase in absorption will raise the surface temperature of the Earth.

The Earth's Tropopause

In our previous post, we noted that the temperature of the atmosphere does not drop by more than a few degrees Centigrade between altitude 12 km and 18 km. We concluded that altitude 15 km corresponds roughly to the atmosphere's tropopause, and therefore marks the top of its convection cycle. Today we consider if there is any significant heat transfer between the tropopause and the upper atmosphere.

The following graph shows the absorption of long-wave radiation by the seventh 3-km layer of the Earth's atmosphere, from altitude 18 km to 21 km. This line is the same as the 18-km line in our Earth's Atmosphere post. The absorption is typical of a clear day in April, at latitude 30°N. We assume water vapor content is zero, but CO2 concentration remains 330 ppm. We assume air pressure is 160 mbar and temperature is 210 K, or −63°C.



In the seventh layer, absorption by CO2 remains strong. As before, we say our 3-km layer is opaque at a particular wavelength when it absorbs more than 63% of that wavelength, and is transparent otherwise. The seventh 3-km layer is opaque from 14.3 to 15.6 μm, while the sixth layer was opaque to 14.3 to 15.7 μm. The seventh layer will absorb roughly 93% of the heat radiated upwards by the CO2 in the sixth layer.

We note that the actual pressure in the Earth's atmosphere at 18 km is closer to 130 mbar. We calculated atmospheric pressure using our constant-temperature model of atmospheric pressure, and this model starts to be increasingly inaccurate in the cold upper layers of the atmosphere.

When we chose our temperatures, we were looking at this plot and rounding to the nearest 10 K. If you look at the plot yourself, you will see that the minimum temperature varies with latitude, and that the minimum spreads over a large range. We see this variation with latitude and the extent of the minimum in plots like this one also. In the case of 30°N, the temperature minimum extends from roughly 12 km to 22 km. The tropopause is the altitude at which the temperature stops dropping with pressure as it would in adiabatic expansion. Thus the tropopause is not at the altitude of minimum temperature, but rather at the altitude where temperature stops dropping adiabatically with pressure.

We go back to this plot and estimate the tropopause altitude as 9 km at 90°N (the north pole), 12 km at 30°N, and 13 km at 0°N (the equator). Why is the tropopause higher in the tropics? Our model of the greenhouse effect and the atmospheric layers must provide us with an answer to this question.

We look at the water vapor concentration in this plot, we see that we have 10 ppm water vapor concentration up to roughly 9 km at 0°N, 12 km at 30°N, and 13 km at 0°N. As we saw in the fifth layer, water vapor concentration of 10 ppm marks the altitude at which the atmosphere becomes transparent to wavelengths 5 to 9 μm, thus allowing the atmosphere below to radiate these wavelengths into space. Between 12 km and 21 km there is no significant change in the absorption spectrum of the atmosphere. A large body of air rising from 12 km to 21 km will be unable to radiate heat into space as it rises. If it cannot radiate heat, it will not sink, and so we will have no convection. Thus we expect the convection cycle to stop at the altitude where water vapor concentration drops to around 10 ppm, and this is indeed what we observe in the Earth's atmosphere.

There is no significant drop in temperature for at least 10 km above the tropopause. Without a temperature gradient, there can be no heat transport by conduction. There is no significant change in the absorption spectrum as we ascend these 10 km, so each layer of the atmosphere will receive as much heat by radiation from the layers above and below as it radiates back to those same layers. Thus there can be no significant heat transport by radiation either. We have already concluded that convection stops at the tropopause, so we see that there is no significant heat exchange between the tropopause and the atmosphere above it.