On 22nd January 2010, the UK parliament's science and technology committee announced an inquiry into Climategate. Steve McIntyre of Climate Audit made this submission to the committee.
In his submission, Mr. McIntyre compares graphs of data that various climatologists attempted to keep private to the graphs of data that these same climatologists published in their papers. The private data shows a prominent medieval warm period. The published data shows no medieval warm period. The published data suggests that the twentieth century warming is unprecedented. The private data shows quite the opposite. Mr. McIntyre also presents the substitution of thermometer measurements for tree-ring proxy measurements by CRU in 1999, and the deletion of post-1960 tree-ring proxy measurements from the published data sets.
I spent ten minutes looking for a similar submission from the authors of Real Climate, but found none. I did, however, note that recent posts on Real Climate are dominated by assertions that the mainstream media, in particular UK newspapers, are doing a bad job reporting on Climategate. In The Guardian Disappoints, Gavin Schmidt talks of a "complete collapse" in reporting standards in the UK. What I can't find anywhere is the sort of succinct refutation that will be necessary to rebut Mr. MacIntyre's submission to parliament.
On the one hand, we have skeptics who believe in the open disclosure of all data, even when the data conflicts with a scientist's beliefs. On the other hand, we have climatologists who believe the best way to present science to the public is to shield them from data that they would otherwise misunderstand, or which would give fuel to the unreasonable arguments of climate skeptics. It may be that climatologists are absolutely right about anthropogenic global warming and its up-coming catastrophic effects. It may be that they are doing the right and moral thing by hiding the decline. But most of us don't like to have other people hiding things from us. We don't like anyone suggesting that a lunatic can get hold of the wrong data and make us believe something absurd. The climatologist's approach to the public may be caring, but it is also disdainful.
Climatologists have so much invested in their theory of anthropogenic global warming that it's unreasonable to expect them to back down and change their way of doing business after Climategate. We, the public who pay their salaries, will eventually insist that they do the job we want them to do in the way we want them to do it. But until that then, climatologists will stick to their existing methods and remain unrepentant.
After all, there are still people out there who believe that crop circles are made by aliens.
UPDATE: Thanks to Chuck for pointing to the submission of the Institute for Physics.
UPDATE: People who study crop circles are called cereologists.
Sunday, February 28, 2010
Friday, February 26, 2010
Radiation, Convection, Conduction
There's a song by Flanders and Swann called First and Second Law. The third verse is:
Heat is work and work is heat
And work is heat and heat is work
Heat will pass by conduction
And heat will pass by convection
And heat will pass by radiation
And that's a physical law
Indeed. But conduction, convection, and radiation get so intimately mixed together that its sometimes hard to say which is which. Convection, for example, always begins with heat passing into a gas by conduction. Without conduction there would be no convection. The converse is not true. And there are cases where convection and radiation look exactly like conduction. One such case is the flow of heat through the filter gas we introduced in our previous post.
Our calculations showed a net 350 W/m2 of heat flowing up through the 1 km Lower Gas as a result of The Body being 6.4°C warmer than the lower surface of the Filter Gas. Of this 350 W/m2, 80% passed by convection and 20% was the imbalance in the long-wave radiation passing between The Body and the Filter Gas. Suppose we cover The Body with a thin sheet of a material that reflects long-wave radiation. By radiative symmetry, The Body no longer emits radiation to the Filter Gas. Nor does it absorb radiation from the Filter Gas. Referring to our earlier diagram, we have EB = EFL = 0 W/m2, so for equilibrium at The Body we must have
QLG = k(TB−TFL)/DLG = ES = 350 W/m2.
With k = 44 kW/mK and DLG = 1 km we get TB−TFL = 8.0°C. When we stop radiation between the Filter Gas and The Body, The Body warms up by 1.6°C. Heat flows by convection only.
But how does heat flow through the Filter Gas? This is where our confusion begins. Certainly, we will have heat flow by convection. But there is also radiation between layers of the Filter Gas. Do we consider this radiation within the Filter Gas to be conduction, or is it something separate? Suppose we cover the lower and upper surfaces of the Filter Gas with a film that is reflecting on the side facing the filter gas, but black on the side facing away from the filter gas. These films absorb and emit long-wave radiation on their outer surfaces, but neither absorb nor emit radiation on their inner surfaces. The Filter Gas itself is aware only of the temperature of the Upper and Lower Films. It receives heat by conduction at the Lower Film. This heat passes up through the Filter Gas by convection, conduction, and also radiation, all operating together, until it arrives at the Upper Film. The heat passes by conduction into the Upper Film and is radiated out into space by the outer surface.
With these films in place, we know that no heat is entering or leaving the Filter Gas by radiation. If the temperature difference across the Filter Gas is 80°C, the distance between the films is 10 km, and 350 W/m2 flows between the films, it looks as if we have a conducting substance between the films with specific conductivity, k, equal to 44 kW/mK. In theory, we could replace our Filter Gas with some other substance with the same specific conductivity.
In practice, there is no substance with specific conductivity even close to 44 kW/mK. The specific conductivity of aluminum is around 200 W/mK. Diamond is around 2 kW/mK. Air is 0.025 W/mK. Specific conductivity refers to the passage of heat through stationary material. To measure the specific conductivity of the Filter Gas, we could use a body of gas that is filled with goose down, so that the gas cannot move up or down. Stationary air is a fine insulator.
But air allowed to move freely in a large volume is a fine transporter of heat. The coefficient of convective heat transfer for air is between 10 and 100 W/m2K, with no mention of the height of the column of air. If we used 10 W/m2K for our Filter Gas, a 35°C temperature difference across the 10-km thickness of the Filter Gas would be sufficient to cause 350 W/m2 to flow. As it is, we assumed an 80°C difference, for similarity with the Earth's atmosphere. We see that convection gives our gas layers the power to transport hundreds of times as much heat as an equivalent thickness of metal.
Does a black gas transport more heat than a transparent gas? Our Filter Gas has some absorption length with respect to long-wave radiation, so consider a layer of Filter Gas that is much thinner than the absorption length. The gas below will radiate upwards and the gas above will radiate downwards. The upward radiation will be greater than the downward radiation because the gas below is warmer than the gas above. A black gas transports more heat than a transparent gas.
How much more heat does a black gas transport? If we consider the contribution of radiation to heat transport from The Body to the Filter Gas for a temperature difference of 6.4°C, we see that radiation adds 20% to the total heat transport. A black gas transports slightly more heat than a transparent gas, but not twice as much.
We can simulate the absorption length of our Filter Gas with a transparent layer of gas on the bottom and the top, which is exactly what we do in our latest model. The Lower Gas represents the absorption length of the warm, dense, lower surface of the Filter Gas, while the Upper Gas represents the absorption length of the cold, sparse, upper surface of the Filter Gas.
Heat is work and work is heat
And work is heat and heat is work
Heat will pass by conduction
And heat will pass by convection
And heat will pass by radiation
And that's a physical law
Indeed. But conduction, convection, and radiation get so intimately mixed together that its sometimes hard to say which is which. Convection, for example, always begins with heat passing into a gas by conduction. Without conduction there would be no convection. The converse is not true. And there are cases where convection and radiation look exactly like conduction. One such case is the flow of heat through the filter gas we introduced in our previous post.
Our calculations showed a net 350 W/m2 of heat flowing up through the 1 km Lower Gas as a result of The Body being 6.4°C warmer than the lower surface of the Filter Gas. Of this 350 W/m2, 80% passed by convection and 20% was the imbalance in the long-wave radiation passing between The Body and the Filter Gas. Suppose we cover The Body with a thin sheet of a material that reflects long-wave radiation. By radiative symmetry, The Body no longer emits radiation to the Filter Gas. Nor does it absorb radiation from the Filter Gas. Referring to our earlier diagram, we have EB = EFL = 0 W/m2, so for equilibrium at The Body we must have
QLG = k(TB−TFL)/DLG = ES = 350 W/m2.
With k = 44 kW/mK and DLG = 1 km we get TB−TFL = 8.0°C. When we stop radiation between the Filter Gas and The Body, The Body warms up by 1.6°C. Heat flows by convection only.
But how does heat flow through the Filter Gas? This is where our confusion begins. Certainly, we will have heat flow by convection. But there is also radiation between layers of the Filter Gas. Do we consider this radiation within the Filter Gas to be conduction, or is it something separate? Suppose we cover the lower and upper surfaces of the Filter Gas with a film that is reflecting on the side facing the filter gas, but black on the side facing away from the filter gas. These films absorb and emit long-wave radiation on their outer surfaces, but neither absorb nor emit radiation on their inner surfaces. The Filter Gas itself is aware only of the temperature of the Upper and Lower Films. It receives heat by conduction at the Lower Film. This heat passes up through the Filter Gas by convection, conduction, and also radiation, all operating together, until it arrives at the Upper Film. The heat passes by conduction into the Upper Film and is radiated out into space by the outer surface.
With these films in place, we know that no heat is entering or leaving the Filter Gas by radiation. If the temperature difference across the Filter Gas is 80°C, the distance between the films is 10 km, and 350 W/m2 flows between the films, it looks as if we have a conducting substance between the films with specific conductivity, k, equal to 44 kW/mK. In theory, we could replace our Filter Gas with some other substance with the same specific conductivity.
In practice, there is no substance with specific conductivity even close to 44 kW/mK. The specific conductivity of aluminum is around 200 W/mK. Diamond is around 2 kW/mK. Air is 0.025 W/mK. Specific conductivity refers to the passage of heat through stationary material. To measure the specific conductivity of the Filter Gas, we could use a body of gas that is filled with goose down, so that the gas cannot move up or down. Stationary air is a fine insulator.
But air allowed to move freely in a large volume is a fine transporter of heat. The coefficient of convective heat transfer for air is between 10 and 100 W/m2K, with no mention of the height of the column of air. If we used 10 W/m2K for our Filter Gas, a 35°C temperature difference across the 10-km thickness of the Filter Gas would be sufficient to cause 350 W/m2 to flow. As it is, we assumed an 80°C difference, for similarity with the Earth's atmosphere. We see that convection gives our gas layers the power to transport hundreds of times as much heat as an equivalent thickness of metal.
Does a black gas transport more heat than a transparent gas? Our Filter Gas has some absorption length with respect to long-wave radiation, so consider a layer of Filter Gas that is much thinner than the absorption length. The gas below will radiate upwards and the gas above will radiate downwards. The upward radiation will be greater than the downward radiation because the gas below is warmer than the gas above. A black gas transports more heat than a transparent gas.
How much more heat does a black gas transport? If we consider the contribution of radiation to heat transport from The Body to the Filter Gas for a temperature difference of 6.4°C, we see that radiation adds 20% to the total heat transport. A black gas transports slightly more heat than a transparent gas, but not twice as much.
We can simulate the absorption length of our Filter Gas with a transparent layer of gas on the bottom and the top, which is exactly what we do in our latest model. The Lower Gas represents the absorption length of the warm, dense, lower surface of the Filter Gas, while the Upper Gas represents the absorption length of the cold, sparse, upper surface of the Filter Gas.
Wednesday, February 24, 2010
Extreme Greenhouse, Part Three
The diagram below shows a body heated by short-wave radiation, ES. The Body is covered by three layers of gas. The Lower and Upper Gas are transparent to both short-wave and long-wave radiation. The Filter Gas is transparent to short-wave radiation but black to long-wave radiation. In later posts, we will see how a layer of transparent gas below a layer of black gas can be used to model the gradual absorption of long-wave radiation in the Earth's atmosphere. As before, we assume our system is in thermal equilibrium, which means that all temperatures are constant. No part of the system is heating up or cooling down.
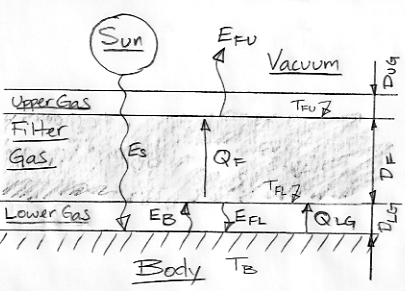
By radiative symmetry, the Upper Gas radiates no heat. Nor can it transport heat into the vacuum by convection or conduction. The temperature of the Upper Gas is constant, so it cannot be gaining or losing heat. It must be at the same temperature as the upper surface of the Filter Gas, which is TFU.
Thermal equilibrium for the entire system dictates that QF = EFU = ES. In our previous post we assumed ES = 350 W/m2 for similarity with the Sun and the Earth, and we showed how Stefan's Law dictates that TFU = 280 K.
We also assumed QF = KF(TFL−TFU) and we chose KF = 4.4 W/m2K. But this equation for QF says nothing about the depth of the filter. Let us now relate the heat flowing through each gas layer to its depth with a single coefficient, k, with units of W/mK.
QF = k(TFL−TFU)/DF, QLG = k(TB−TFL)/DLG
For k, let's choose 350 W/m2 / 80 K × 10 km = 44 kW/mK. We choose 80 K because that's roughly the drop across the Earth's troposphere, and we choose 10 km because that's roughly the altitude of the Earth's tropopause. With DF = 10 km and QF = 350 W/m2 we have TFL−TFU = 80 K, so that TFL = 360 K.
Let us consider thermal equilibrium at The Body surface. We must have ES + EFL = EB + QLG. We apply Stefan's Law to obtain the following.
ES + σ(TFL)4 = σ(TB)4 + k(TB−TFL)/DLG
Where σ = 5.7×10−8 W/m2K4 and k = 44 kW/mK. Suppose we assume DLG = 1 km. We have already calculated that TFL = 360 K, so we arrive at the following relation for TB.
(TB)4.(5.7×10−8 W/m2K4) + TB.(44 W/m2K) = 17 kW/m2
The solution to this equation is TB = 366.4 K = 94.5°C. With a vacuum in place of the Lower Gas, we found TB = 390 K = 117°C. Thus the addition of the Lower Gas reduced the temperature of The Body by 24°C. At this temperature, EB = 1.03 kW/m2 and EFL = 960 W/m2, so that The Body is radiating 70 W/m2 more heat to the Filter Gas than the Filter Gas is radiating back to The Body. But QLG = 280 W/m2. Convection accounts for 80% of the net 350 W/m2 passing from The Body to the Filter Gas. Imbalance in radiative transfer accounts for only 20%.
In future posts, we will see how our three-layer gas model can be used to approximate heat transfer through the Earth's atmosphere, and allow us to estimate the influence of carbon dioxide concentration upon the Earth's temperature.

By radiative symmetry, the Upper Gas radiates no heat. Nor can it transport heat into the vacuum by convection or conduction. The temperature of the Upper Gas is constant, so it cannot be gaining or losing heat. It must be at the same temperature as the upper surface of the Filter Gas, which is TFU.
Thermal equilibrium for the entire system dictates that QF = EFU = ES. In our previous post we assumed ES = 350 W/m2 for similarity with the Sun and the Earth, and we showed how Stefan's Law dictates that TFU = 280 K.
We also assumed QF = KF(TFL−TFU) and we chose KF = 4.4 W/m2K. But this equation for QF says nothing about the depth of the filter. Let us now relate the heat flowing through each gas layer to its depth with a single coefficient, k, with units of W/mK.
QF = k(TFL−TFU)/DF, QLG = k(TB−TFL)/DLG
For k, let's choose 350 W/m2 / 80 K × 10 km = 44 kW/mK. We choose 80 K because that's roughly the drop across the Earth's troposphere, and we choose 10 km because that's roughly the altitude of the Earth's tropopause. With DF = 10 km and QF = 350 W/m2 we have TFL−TFU = 80 K, so that TFL = 360 K.
Let us consider thermal equilibrium at The Body surface. We must have ES + EFL = EB + QLG. We apply Stefan's Law to obtain the following.
ES + σ(TFL)4 = σ(TB)4 + k(TB−TFL)/DLG
Where σ = 5.7×10−8 W/m2K4 and k = 44 kW/mK. Suppose we assume DLG = 1 km. We have already calculated that TFL = 360 K, so we arrive at the following relation for TB.
(TB)4.(5.7×10−8 W/m2K4) + TB.(44 W/m2K) = 17 kW/m2
The solution to this equation is TB = 366.4 K = 94.5°C. With a vacuum in place of the Lower Gas, we found TB = 390 K = 117°C. Thus the addition of the Lower Gas reduced the temperature of The Body by 24°C. At this temperature, EB = 1.03 kW/m2 and EFL = 960 W/m2, so that The Body is radiating 70 W/m2 more heat to the Filter Gas than the Filter Gas is radiating back to The Body. But QLG = 280 W/m2. Convection accounts for 80% of the net 350 W/m2 passing from The Body to the Filter Gas. Imbalance in radiative transfer accounts for only 20%.
In future posts, we will see how our three-layer gas model can be used to approximate heat transfer through the Earth's atmosphere, and allow us to estimate the influence of carbon dioxide concentration upon the Earth's temperature.
Wednesday, February 17, 2010
Extreme Greenhouse, Part Two
According to atmospheric science sites like this one, atmospheric temperature drops by roughly 80°C as we ascent from altitude 0 km to 10 km. The drop is almost linear, meaning it has constant gradient −8°C/km. At 10 km the temperature stops dropping. The region in which the temperature drops linearly with altitude is the troposphere. Above that is the stratosphere. The boundary between the two is the tropopause.
Consider again our diagram of the extreme greenhouse (we invite you to open the diagram in a new window so you can look at it while you read on). In our previous post, we assumed the filter was a perfect conductor. Let's assume now that the filter presents some thermal resistance. We need TFL > TFU so that heat will flow up through the filter to the top surface, where it will be radiated into space. We have,
QF = KF(TFL-TFU) = EFU = ES,
where QF is the heat passing up through the filter. The temperature within the filter will have a constant, negative gradient with altitude. In the case of the Earth and the Sun, we have already shown that ES (the heat from the sun) is 350 W/m2, so that TFU = 280 K. Now suppose KF = 350 Wm−2 / 80 K = 4.4 W/m2K, which will give us an 80°C drop in temperature through the filter, the same drop we see going up through the troposphere. Now we see that TFL = 360 K. By Stefan's Law, EFL = 960 Wm−2. For thermal equilibrium at the body surface, we must have EB = EFL + ES = 1.3 kWm−2, which implies that we have TB = 390 K = 117 °C.
Let us imagine the filter in our extreme greenhouse is close to the surface of our body. Recall that we assumed a vacuum between the filter and the body, so that heat transfer between the two must take place by radiation alone. With our chosen value of filter conductivity, we see that the presence of the filter warms our body from 280 K to 390 K, a total of 110 K.
Next we will consider what happens if we allow the filter to come into physical contact with the body, so that heat can pass between the two by conduction, convection, and evaporation as well as by radiation. In that case, we will see that the filter is less able to warm the body.
Consider again our diagram of the extreme greenhouse (we invite you to open the diagram in a new window so you can look at it while you read on). In our previous post, we assumed the filter was a perfect conductor. Let's assume now that the filter presents some thermal resistance. We need TFL > TFU so that heat will flow up through the filter to the top surface, where it will be radiated into space. We have,
QF = KF(TFL-TFU) = EFU = ES,
where QF is the heat passing up through the filter. The temperature within the filter will have a constant, negative gradient with altitude. In the case of the Earth and the Sun, we have already shown that ES (the heat from the sun) is 350 W/m2, so that TFU = 280 K. Now suppose KF = 350 Wm−2 / 80 K = 4.4 W/m2K, which will give us an 80°C drop in temperature through the filter, the same drop we see going up through the troposphere. Now we see that TFL = 360 K. By Stefan's Law, EFL = 960 Wm−2. For thermal equilibrium at the body surface, we must have EB = EFL + ES = 1.3 kWm−2, which implies that we have TB = 390 K = 117 °C.
Let us imagine the filter in our extreme greenhouse is close to the surface of our body. Recall that we assumed a vacuum between the filter and the body, so that heat transfer between the two must take place by radiation alone. With our chosen value of filter conductivity, we see that the presence of the filter warms our body from 280 K to 390 K, a total of 110 K.
Next we will consider what happens if we allow the filter to come into physical contact with the body, so that heat can pass between the two by conduction, convection, and evaporation as well as by radiation. In that case, we will see that the filter is less able to warm the body.
Sunday, February 14, 2010
Medieval Warm Period
Dr. Phil Jones, former director of CRU (Climatic Research Unit) at UAE (University of East Anglia), granted an interview of sorts to the BBC. They sent him questions, and he answered them, including links to graphs. You will find the complete exchange here. Dr. Jones is at the center of the Climategate affair. His answers to the BBC seem sincere and thorough to me. The last few months must have been hard on Dr. Jones. I'm glad to see him talking to the press. The BBC's questions were pointed. There is no sign of the global warming zealotry that I had come to expect from the BBC. I'm sure Climategate has been hard on the global warming zealots as well. But the BBC appears to be responding by putting their journalistic principles first.
Of particular importance to the debate over the Hockey Stick graph and its associated Mann-Made Warming, is the existence or non-existence of the Medieval Warm Period (MWP). The BBC asked Dr. Jones if the MWP was warmer than today, and here's his answer.
"There is much debate over whether the Medieval Warm Period was global in extent or not. The MWP is most clearly expressed in parts of North America, the North Atlantic and Europe and parts of Asia. For it to be global in extent the MWP would need to be seen clearly in more records from the tropical regions and the Southern Hemisphere. There are very few palaeoclimatic records for these latter two regions."
Indeed: there is plenty of evidence in the Northern Hemisphere that the MWP was 2°C warmer than today. Even the IPPC said as much back in 1995, before the Hockey Stick graph was published. Whether or not we need evidence from the Southern Hemisphere to believe in the MWP is a matter of opinion. If it were possible for the Northern Hemisphere to warm 2°C while leaving the Southern Hemisphere unchanged, this would suggest that a 2°C warming can be both natural and local. If the MWP were global, we see that a 2°C warming can be natural. Either way, the Northern Hemisphere's MWP is evidence that 2°C warming from current temperatures can occur naturally.
Dr. Jones's full answer shows that he understands the implications of the MWP. In another answer, he says there has been no statistically significant warming since 1995, but he adds that, "This trend (0.12C per decade) is positive, but not significant at the 95% significance level. The positive trend is quite close to the significance level." Reports of Dr. Jones performing a U-Turn appear to be over-blown. But at least he is talking.
Of particular importance to the debate over the Hockey Stick graph and its associated Mann-Made Warming, is the existence or non-existence of the Medieval Warm Period (MWP). The BBC asked Dr. Jones if the MWP was warmer than today, and here's his answer.
"There is much debate over whether the Medieval Warm Period was global in extent or not. The MWP is most clearly expressed in parts of North America, the North Atlantic and Europe and parts of Asia. For it to be global in extent the MWP would need to be seen clearly in more records from the tropical regions and the Southern Hemisphere. There are very few palaeoclimatic records for these latter two regions."
Indeed: there is plenty of evidence in the Northern Hemisphere that the MWP was 2°C warmer than today. Even the IPPC said as much back in 1995, before the Hockey Stick graph was published. Whether or not we need evidence from the Southern Hemisphere to believe in the MWP is a matter of opinion. If it were possible for the Northern Hemisphere to warm 2°C while leaving the Southern Hemisphere unchanged, this would suggest that a 2°C warming can be both natural and local. If the MWP were global, we see that a 2°C warming can be natural. Either way, the Northern Hemisphere's MWP is evidence that 2°C warming from current temperatures can occur naturally.
Dr. Jones's full answer shows that he understands the implications of the MWP. In another answer, he says there has been no statistically significant warming since 1995, but he adds that, "This trend (0.12C per decade) is positive, but not significant at the 95% significance level. The positive trend is quite close to the significance level." Reports of Dr. Jones performing a U-Turn appear to be over-blown. But at least he is talking.
Wednesday, February 10, 2010
Extreme Greenhouse
We continue our consideration of the atmospheric greenhouse effect with an extreme example, in which we maximize the effect. The diagram below shows the surface of a body which is covered by vacuum, surrounded by a filter, and illuminated by a sun. By virtue of its high surface temperature, the sun emits short-wave radiation, let us say, between 0.2 μm and 2 μm, while the body, by virtue of its lower surface temperature, emits long-wave radiation, let us say, between 6 μm and 30 μm. (See our earlier Black Bodies post for explanations of these wavelengths.)
The filter is so-called because it allows short-wave radiation to pass through without loss, but absorbs all long-wave radiation immediately upon entering. By radiative symmetry, the filter cannot radiate at all at short wavelengths, but is a perfect radiator of long wavelengths. The body itself we assume is a perfect absorber of short-wave radiation and a perfect emitter of long-wave radiation. Which is to say: it is black to both short-wave and long-wave radiation.
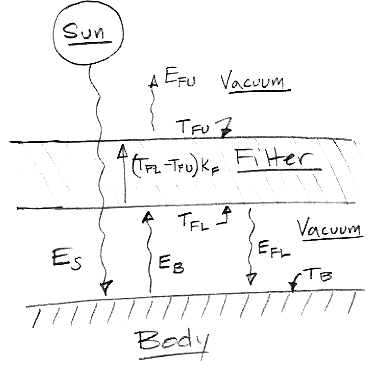
The squiggly lines are radiation, denoted E with an appropriate subscript: S for sun, B for body, FL for filter lower surface, and FU for filter upper surface. We measure radiation in units of W/m2. We have temperatures marked also, denoted T. There is heat flow by conduction within the filter, amounting to KF(TFL−TFU), where F is the conductivity of the filter in W/Km2. The only heat flow from the body to the filter is by radiation, because the two are separated by a vacuum.
We assume that all parts of our system are in thermal equilibrium, which is to say that their temperature is constant, so that there is as much heat leaving them as entering them. We assume there is no way for heat to leave the body except through its top surface, which would be the case if the top surface wrapped around upon itself as does the surface of a sphere.
Let's start with the simple case where the filter is a perfect conductor, so that TFL = TFU (KF is infinite). The top and bottom surfaces are black-body radiators, so they both emit the same amount of long-wave radiation. Thus EFL = EFU. Meanwhile, we must have as much heat leaving our system as entering, so ES = EFU. At the same time, we must have equal heat entering and leaving the body itself, so ES + EFL = 2EFL = EB. The power radiated by the body is a factor of two greater than the power arriving from the sun.
Radiated power is related to temperature by Stefan's Law. With σ as Stefan's constant, we have EB = σ(TB)4 = 2EFL = σ(TFL)4, from which we conclude TB = 21/4TFL = 1.19TFL. But TFL = TFU, and we can determine TFU by noting that ES = EFU = σ(TFU)4, which yields TFU = (ES/σ)1/4. As we showed in Solar Heat, in the case of the Sun and the Earth, we have ES = 350 W/m2. With 350 W/m2 arriving from the sun, we would have, in our example construction, TFU = 280 K = 7°C and TB = 333 K = 60°C. The presence of the filter raises the temperature of our body by 53°C.
The greenhouse heating of a black body when we place a perfectly-conducting greenhouse filter between the body and a source of short-wave radiation is 19% of its equilibrium absolute temperature without the filter. Furthermore, in these particular circumstances, the heat radiated by the warmed body is exactly twice that radiated into space by the filter, and twice that received from the source of short-wave radiation.
The filter is so-called because it allows short-wave radiation to pass through without loss, but absorbs all long-wave radiation immediately upon entering. By radiative symmetry, the filter cannot radiate at all at short wavelengths, but is a perfect radiator of long wavelengths. The body itself we assume is a perfect absorber of short-wave radiation and a perfect emitter of long-wave radiation. Which is to say: it is black to both short-wave and long-wave radiation.

The squiggly lines are radiation, denoted E with an appropriate subscript: S for sun, B for body, FL for filter lower surface, and FU for filter upper surface. We measure radiation in units of W/m2. We have temperatures marked also, denoted T. There is heat flow by conduction within the filter, amounting to KF(TFL−TFU), where F is the conductivity of the filter in W/Km2. The only heat flow from the body to the filter is by radiation, because the two are separated by a vacuum.
We assume that all parts of our system are in thermal equilibrium, which is to say that their temperature is constant, so that there is as much heat leaving them as entering them. We assume there is no way for heat to leave the body except through its top surface, which would be the case if the top surface wrapped around upon itself as does the surface of a sphere.
Let's start with the simple case where the filter is a perfect conductor, so that TFL = TFU (KF is infinite). The top and bottom surfaces are black-body radiators, so they both emit the same amount of long-wave radiation. Thus EFL = EFU. Meanwhile, we must have as much heat leaving our system as entering, so ES = EFU. At the same time, we must have equal heat entering and leaving the body itself, so ES + EFL = 2EFL = EB. The power radiated by the body is a factor of two greater than the power arriving from the sun.
Radiated power is related to temperature by Stefan's Law. With σ as Stefan's constant, we have EB = σ(TB)4 = 2EFL = σ(TFL)4, from which we conclude TB = 21/4TFL = 1.19TFL. But TFL = TFU, and we can determine TFU by noting that ES = EFU = σ(TFU)4, which yields TFU = (ES/σ)1/4. As we showed in Solar Heat, in the case of the Sun and the Earth, we have ES = 350 W/m2. With 350 W/m2 arriving from the sun, we would have, in our example construction, TFU = 280 K = 7°C and TB = 333 K = 60°C. The presence of the filter raises the temperature of our body by 53°C.
The greenhouse heating of a black body when we place a perfectly-conducting greenhouse filter between the body and a source of short-wave radiation is 19% of its equilibrium absolute temperature without the filter. Furthermore, in these particular circumstances, the heat radiated by the warmed body is exactly twice that radiated into space by the filter, and twice that received from the source of short-wave radiation.
Miskolczi's Theorem
A former employee of NASA, Ferene M. Miskolczi, published a paper Greenhouse effect in semi-transparent planetary atmospheres, in which he argues that the long-wave radiation from the planet surface is 1.5 times the long-wave radiation from the upper surface of the atmosphere. He uses this factor of 1.5, together with some mathematics that we have not studies, to show that the warming due to the greenhouse effect in a semi-transparent atmosphere is inherently self-stabilizing, and claims that addition of CO2 to the atmosphere will result in a decrease in water vapor content so as to restore the warming to its stable value.
You will find Dr. Miskolczi's paper reviewed in detail at Niche Modeling. Our friend Peter Newnam pointed us to the paper and we started going through it a few days ago. We follow his argument up to and including his equation (6), but when he comes to equation (7), he loses us. Try as we might, we cannot understand how "The principle of conservation of energy dictates that" his equation (7) holds. Nor are we convinced of equation (7) by the review at Niche Modeling.
Having said that, we see that Dr. Miskolczi arrived at his conclusion from his examination of atmospheric data while working at NASA. It appears that his equation (7), together with some other mathematical work, produce a theorem that is consistent with his observations. We will keep Dr. Miskolczi's theorem in mind as we explore the Greenhouse Effect in further posts.
You will find Dr. Miskolczi's paper reviewed in detail at Niche Modeling. Our friend Peter Newnam pointed us to the paper and we started going through it a few days ago. We follow his argument up to and including his equation (6), but when he comes to equation (7), he loses us. Try as we might, we cannot understand how "The principle of conservation of energy dictates that" his equation (7) holds. Nor are we convinced of equation (7) by the review at Niche Modeling.
Having said that, we see that Dr. Miskolczi arrived at his conclusion from his examination of atmospheric data while working at NASA. It appears that his equation (7), together with some other mathematical work, produce a theorem that is consistent with his observations. We will keep Dr. Miskolczi's theorem in mind as we explore the Greenhouse Effect in further posts.
Sunday, February 7, 2010
Climategate Commentary
Our correspondent Peter Newnam points us to an article in The Spectator, The global warming guerrillas, which summarizes the consequences of Climategate for the Anthropogenic Global Warming movement, and also discusses the role of blogs and amateurs in the investigation of various claims made by the leaders of the movement.
It was not Private Eye, or the BBC or the News of the World, but a retired electrical engineer in Northampton, David Holland, whose freedom-of-information requests caused the Climategate scientists to break the law, according to the Information Commissioner. By contrast, it has so far attracted little attention that the leaked emails of Climategate include messages from reporters obsequiously seeking ammunition against the sceptics. Other emails have shown reporters meekly changing headlines to suit green activists, or being threatened with ostracism for even reporting the existence of a sceptical angle: ‘Your reportage is very worrisome to most climate scientists,’ one normally alarmist reporter was told last year when he slipped briefly off message. ‘I sense that you are about to experience the “Big Cutoff” from those of us who believe we can no longer trust you, me included.’
With only one or two dozen readers, this blog is not at the forefront of the debate, but we nevertheless feel like we are in good company. We will continue our Home Climate Analysis for the pleasure of it, and because we feel part of a change in the way science is reviewed.
UPDATE: Conflict of interest over at The BBC.
UPDATE: Following Glaciergate we now have Africagate.
It was not Private Eye, or the BBC or the News of the World, but a retired electrical engineer in Northampton, David Holland, whose freedom-of-information requests caused the Climategate scientists to break the law, according to the Information Commissioner. By contrast, it has so far attracted little attention that the leaked emails of Climategate include messages from reporters obsequiously seeking ammunition against the sceptics. Other emails have shown reporters meekly changing headlines to suit green activists, or being threatened with ostracism for even reporting the existence of a sceptical angle: ‘Your reportage is very worrisome to most climate scientists,’ one normally alarmist reporter was told last year when he slipped briefly off message. ‘I sense that you are about to experience the “Big Cutoff” from those of us who believe we can no longer trust you, me included.’
With only one or two dozen readers, this blog is not at the forefront of the debate, but we nevertheless feel like we are in good company. We will continue our Home Climate Analysis for the pleasure of it, and because we feel part of a change in the way science is reviewed.
UPDATE: Conflict of interest over at The BBC.
UPDATE: Following Glaciergate we now have Africagate.
CO2 Spectrum
After three weeks of searching, we found a carbon dioxide (CO2) spectrum on the web here at the NIST site. The spectrum was measured in 1964, and the original graph was digitally scanned. You will find the raw numbers here. The data gives transmission as a fraction for infrared light betwen 2.63 μm (3797.207 1/cm) and 21.79 μm (458.879 1/cm). The chemists measured transmission through a 10-cm chamber containing one third CO2 and two-thirds N2 (nitrogen) at 0.789 bar pressure (78.9% of sea-level atmospheric pressure).
We converted the transmission values into absorption length for pure CO2 at standard temperature and pressure (20°C and 101 kPa). The absorption length (or penetration depth) is the value L in the Beer-Lambert Law of transmission through an absorbing medium. We have A = 1 − e−x/L, where A is the fraction absorbed and x is depth. You will find our plot of the spectrum in our Climate.xls spreadsheet, which is in Climate.zip.
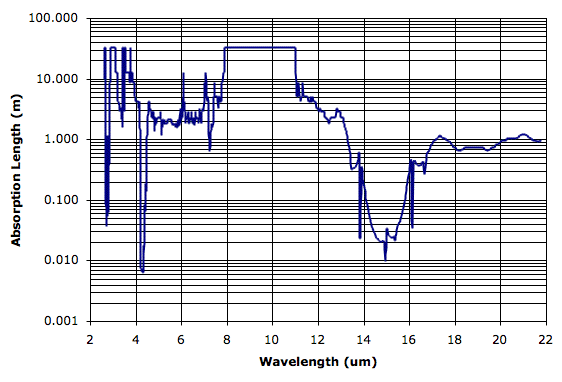
The flat-topped parts of the spectrum are where the original measurements are unable to detect any absorption by CO2 along the 10-cm path, and we have capped the spectrum at around 33 m, which corresponds to transmission of 0.999 in the original data.
We hope to use this spectrum to inform us of CO2's role in the greenhouse effect. We can use the atmospheric concentration of CO2 to determine the absorption length of atmospheric CO2. Before we do that, however, we see that pure CO2 has absorption length greater than 1 m between 5 μm and 13 μm. In our previous post we saw how the Earth's atmosphere is transparent between 8 μm and 13 μm. At 13 μm, the CO2 absorption length plunges by two orders of magnitude until it reaches a low of 10 cm at 14.92 μm. We are still looking for a good water-vapor spectrum, which will allow us to compare the role of CO2 to that of water-vapor in atmospheric absorption. But it looks likely that CO2 is responsible for atmospheric absorption in the 13-μm to 16-μm band.
UPDATE: You will find the text data for the above plot in the CO2 sheet of Climate.xls in Climate.zip. For water-vapor spectrum see Continuum Absorption Length. For the spectrum of diluted CO2 in air, see CO2 Continuum.
We converted the transmission values into absorption length for pure CO2 at standard temperature and pressure (20°C and 101 kPa). The absorption length (or penetration depth) is the value L in the Beer-Lambert Law of transmission through an absorbing medium. We have A = 1 − e−x/L, where A is the fraction absorbed and x is depth. You will find our plot of the spectrum in our Climate.xls spreadsheet, which is in Climate.zip.

The flat-topped parts of the spectrum are where the original measurements are unable to detect any absorption by CO2 along the 10-cm path, and we have capped the spectrum at around 33 m, which corresponds to transmission of 0.999 in the original data.
We hope to use this spectrum to inform us of CO2's role in the greenhouse effect. We can use the atmospheric concentration of CO2 to determine the absorption length of atmospheric CO2. Before we do that, however, we see that pure CO2 has absorption length greater than 1 m between 5 μm and 13 μm. In our previous post we saw how the Earth's atmosphere is transparent between 8 μm and 13 μm. At 13 μm, the CO2 absorption length plunges by two orders of magnitude until it reaches a low of 10 cm at 14.92 μm. We are still looking for a good water-vapor spectrum, which will allow us to compare the role of CO2 to that of water-vapor in atmospheric absorption. But it looks likely that CO2 is responsible for atmospheric absorption in the 13-μm to 16-μm band.
UPDATE: You will find the text data for the above plot in the CO2 sheet of Climate.xls in Climate.zip. For water-vapor spectrum see Continuum Absorption Length. For the spectrum of diluted CO2 in air, see CO2 Continuum.
Tuesday, February 2, 2010
Multiple Radiating Surfaces
In Earth Radiator we argued that water vapor in the Earth's atmosphere would absorb all the Earth's radiation, so that the radiating surface of the Earth, as seen from outer-space, would be the upper layers of an atmosphere that is black to infrared. Our argument was based upon the assumption that water vapor would have the same absorption spectrum as liquid water. In Vapor Versus Liquid we showed how this assumption about water vapor was incorrect.
The following graph shows the total transmission of radiation above a mountain and above a jet flying at 12,500 m. We took the graph from SOPHIA, Becklin et al. The authors of the graph assume 1 mm of water above the mountain and 10 μm above the jet (we refer here to the depth of liquid water sufficient to provide the water vapor).
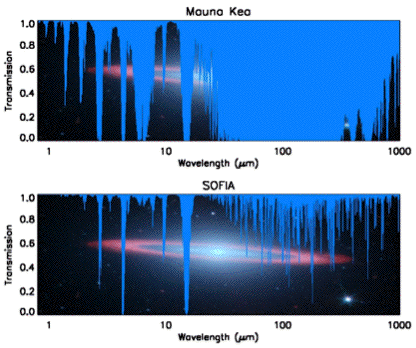
Despite the galaxy in the background, we like this graph because it is not smoothed out like the others we have found. Because the upper graph corresponds to a hundred times more water vapor than the lower graph, the absorption it shows is a hundred times greater. The lower 1000 m of the Earth's atmosphere will almost always contain well over 10 mm of water vapor, so absorption in the entire thickness of the Earth's atmosphere will almost always be ten times greater than in the upper graph.
From these graphs, it appears that Earth's atmosphere is transparent to most wavelengths in the range 8−13 μm. For detail of the transparent band, see our previous post. Looking at one of our earlier graphs, we see that the Earth's radiation lies almost entirely within the range 6−30 μm. The atmosphere is transparent to 8−13 μm, but black to 6−8 μm and 13−30 μm. To the first approximation, the cloudless atmosphere is transparent to the Earth's radiation in the band 8−13 μm, and black elsewhere.
When there are no clouds above the Earth's surface, radiation within the 8−13 μm band will travel straight through the atmosphere and into space. Radiation outside this band will be absorbed. The upper atmosphere, meanwhile, will radiate its own heat into space. According to the principle of radiative symmetry, the atmosphere will radiate only at wavelengths where it is not transparent. Thus a cloudless atmosphere will be radiating heat of wavelengths 6−8 μm and 13−30 μm, but none in the range 8−13 μm.
We must ask ourselves if the surface of the Earth is a good radiator at wavelengths 8−13 μm. Two thirds of the Earth is covered with water, and we have already seen that water is black to all infrared frequencies. By radiative symmetry, the oceans will be black-body emitters of infrared. Those parts of the earth covered by snow and ice will be the same. We are not sure about trees and rock and sand, but taken as a whole, we conclude that the Earth's surface is a good black-body radiator of infrared.
So far we have considered an atmosphere without clouds. But if the atmosphere contains clouds, these will absorb all the Earth's radiation. Clouds contain microscopic drops of water, and liquid water is indeed black to all infrared frequencies. And the clouds will radiate at all infrared frequencies, just like the Earth. Their radiation will be absorbed by the upper atmosphere in the same way as the Earth's radiation.
Let us look at the behavior of the Earth with respect to 12-μm infrared, to which the cloudless atmosphere is transparent. The sun's radiation contains hardly any 12-μm infrared. The Earth's radiation contains plenty of 12-μm infrared. From outer space, we will see 12-μm radiation coming directly from the Earth's surface through a cloudless atmosphere, or we will see 12-μm radiation coming from cloud-tops.
Consider 20-μm infrared, to which the cloudless atmosphere is black. Very little 20-μm infrared arrives from the sun, but the Earth emits plenty of it. All of it is absorbed by the atmosphere. From outer-space, we will see 20-μm radiation from the upper layers of the atmosphere only.
Tthe Earth has three possible radiating surfaces: the upper atmosphere, the cloud-tops, or the surface of the Earth itself. In our next post, we will consider how these three surfaces influence the The Greenhouse Effect.
The following graph shows the total transmission of radiation above a mountain and above a jet flying at 12,500 m. We took the graph from SOPHIA, Becklin et al. The authors of the graph assume 1 mm of water above the mountain and 10 μm above the jet (we refer here to the depth of liquid water sufficient to provide the water vapor).

Despite the galaxy in the background, we like this graph because it is not smoothed out like the others we have found. Because the upper graph corresponds to a hundred times more water vapor than the lower graph, the absorption it shows is a hundred times greater. The lower 1000 m of the Earth's atmosphere will almost always contain well over 10 mm of water vapor, so absorption in the entire thickness of the Earth's atmosphere will almost always be ten times greater than in the upper graph.
From these graphs, it appears that Earth's atmosphere is transparent to most wavelengths in the range 8−13 μm. For detail of the transparent band, see our previous post. Looking at one of our earlier graphs, we see that the Earth's radiation lies almost entirely within the range 6−30 μm. The atmosphere is transparent to 8−13 μm, but black to 6−8 μm and 13−30 μm. To the first approximation, the cloudless atmosphere is transparent to the Earth's radiation in the band 8−13 μm, and black elsewhere.
When there are no clouds above the Earth's surface, radiation within the 8−13 μm band will travel straight through the atmosphere and into space. Radiation outside this band will be absorbed. The upper atmosphere, meanwhile, will radiate its own heat into space. According to the principle of radiative symmetry, the atmosphere will radiate only at wavelengths where it is not transparent. Thus a cloudless atmosphere will be radiating heat of wavelengths 6−8 μm and 13−30 μm, but none in the range 8−13 μm.
We must ask ourselves if the surface of the Earth is a good radiator at wavelengths 8−13 μm. Two thirds of the Earth is covered with water, and we have already seen that water is black to all infrared frequencies. By radiative symmetry, the oceans will be black-body emitters of infrared. Those parts of the earth covered by snow and ice will be the same. We are not sure about trees and rock and sand, but taken as a whole, we conclude that the Earth's surface is a good black-body radiator of infrared.
So far we have considered an atmosphere without clouds. But if the atmosphere contains clouds, these will absorb all the Earth's radiation. Clouds contain microscopic drops of water, and liquid water is indeed black to all infrared frequencies. And the clouds will radiate at all infrared frequencies, just like the Earth. Their radiation will be absorbed by the upper atmosphere in the same way as the Earth's radiation.
Let us look at the behavior of the Earth with respect to 12-μm infrared, to which the cloudless atmosphere is transparent. The sun's radiation contains hardly any 12-μm infrared. The Earth's radiation contains plenty of 12-μm infrared. From outer space, we will see 12-μm radiation coming directly from the Earth's surface through a cloudless atmosphere, or we will see 12-μm radiation coming from cloud-tops.
Consider 20-μm infrared, to which the cloudless atmosphere is black. Very little 20-μm infrared arrives from the sun, but the Earth emits plenty of it. All of it is absorbed by the atmosphere. From outer-space, we will see 20-μm radiation from the upper layers of the atmosphere only.
Tthe Earth has three possible radiating surfaces: the upper atmosphere, the cloud-tops, or the surface of the Earth itself. In our next post, we will consider how these three surfaces influence the The Greenhouse Effect.
Subscribe to:
Comments (Atom)
