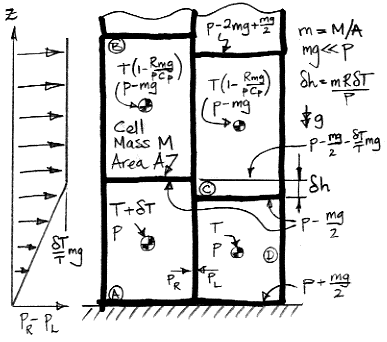
If we ignore kinetic energy, the specific enthalpy of a gas (that's the enthalpy per kilogram) is CpT + gz, where z is the altitude of the cell. When we heat up cell A by δT we increase its specific enthalpy by ΔH1.
ΔH1 = δTCp+gδh/2
This is the energy required to bring about the change in the temperature of cell A, and includes the work required to raise up the cells above A as well as the work required to increase the internal energy of A, and the work required to raise A's own weight.
For an ideal gas cell, we have pV=MRT, and from this we deduce that δh = mRδT/p, where m is the mass per square meter of the cell's bottom surface. Thus we have the following expression for ΔH1.
ΔH1 = δT(Cp+mgR/2p)
When cell A rises, it cools by adiabatic expansion. It is now warmer by δT ' than cell B, and taller by δh'. Suppose we now allow A to cool by δT ', so that it becomes identical to cell B. Its enthalpy decreases by ΔH2, and the four cells and the gas above are in an identical state to the one they were in before we warmed cell A.
ΔH2 = δT 'Cp+gδh'/2
In buoyancy work we showed that δT ' = δT(1−Rmg/pCp). We also showed that δh' ≈ mRδT(1 + mgCv/pCp)/p. Using these relations, and the fact that mg≪p, we obtain the following expression for ΔH2 after several lines of simplification.
ΔH2 = δT(Cp−mgR/2p)
The expressions for ΔH1 and ΔH2 are identical, except the sign of the gravitational term is opposite. When subtract ΔH2 from ΔH1, we obtain the enthalpy per kilogram of cell A that has gone missing during the rotation.
ΔH1−ΔH2 = mgRδT/p = gδh
Enthalpy cannot go missing. Our expression for enthalpy ignores the kinetic energy of the cells when it should not. The kinetic energy of the cells after the rotation is equal to the enthalpy that is missing in our calculation. When we divide it among the mass of the four cells, the missing enthalpy is gδh/4, which is our impetus for circulation.
We performed the same enthalpy calculation for incompressible cells and obtained the same answer. We have arrived at the same expression for impetus by two different means, for both incompressible and compressible cells. We are now confident that our calculation is correct.

I think that, may be, it is better to proceed step by step taking into account the whole column of the cells array initially at the same temperature.
ReplyDelete1) The bottom cell is heated at constant pressure and expands becoming taller by δh1: the cell itself and the entire column increase their geopotential energy.
2) The cell becomes buoyant and rises one row changing its place with the neighboring one above it and only the energy of these cells changes decreasing.
3) The cold cell, once it is arrived at the bottom, is compressed by the cells above it and its height becomes shorter by δh3 inducing the change of its energy and that of all the cells above.
4) The warm cell, arose one step, expands becoming taller by δh4 and working on the cells. The energy of the cells and of the column above changes.
Every time a cell expands or it is compressed changes the energy of the whole column whereas when the cell rises by buoyancy only the energy of the two involved cells is affected. So the global balance of the works and the energies needs to take into account at least one column of the array.
It is possible to compute all the contributes for each step. I tried to do it but it is tedious.
Michele
Dear Michele,
ReplyDeleteIn your step (1), the increase in the enthalpy of the bottom cell is mCpδT1 + mδh1/2 per square meter of base area, where m is the mass per square meter of base area.
This increase in enthalpy is exactly equal to the increase in the internal energy of the cell (that's mCvδT1) plus the increase in its gravitational energy (that's mgδh1/2, where m is mass per square meter of base area) plus the increase in the gravitational energy of all the cells above (that's mRδT, which is equal to the work done against pressure as the cell expands, assuming it is an ideal gas).
In other words: the gravitational potential energy of the gas above is equal to the increase in pV = mRT, which is accounted for by the pressure energy term in the enthalpy calculation.
Thus we can perform a complete calculation by looking only at the changes in the enthalpy of the two bottom cells.
Yours, Kevan
I try to compute the change of the energies with respect to the first and second cell of the column.
ReplyDeleteCell01
- p01=p ; h01=h ; T01=T
- T → T+δT ; p=const ; h → h+δh=h+δT/T0
- it rises and expands ; p → p-mg;
h+δh→(h+δh)[1+(Cv/Cp)mg/p] = (h+δh)(1+β)=hf1;
T+δT→(T+δT)[1-(Cp-Cv)/Cp)mg/p] = (T+δT)(1-ε)= Tf1
Cell02
- p02=p-mg ; h02=h(1+mg/p)= h(1+α) ; T02=T
- it falls and is compressed ; p-mg → p ;
T→T[1+((Cp-Cv)/Cp)mg/p]=T(1+ε)=Tf2 ;
h(1+α)→h(1+α)(1-β)=hf2
Initial specific thermal energy of the cells Ethi=2CvT
Initial specific potential energy of the cells Epi=gh(4+α)/2
Final specific thermal energy of the cells Ethf=Cv(Tf1+Tf2)=Cv[(T+δT)(1-ε)+T(1+ε)=2CvT+ δT(1-ε)
Final specific potential energy of the cells Epf =g[3 h(1+α)(1-β)+ (h+δh)(1+β)]/2= gh(4+α)/2+g[h(2α-2β-3αβ)+ δh(1+β)]/2
The global change of the energy results
ΔE= δT(1-ε)+g[h(2α-2β-3αβ)+ δh+δhβ]/2
As both αβ and δhβ are negligible
ΔE= δT(1-ε)+g[2h(α-β)+ δhβ]/2= δT(1-ε)+g[2h(Cp-Cv)α/Cp+ δhCvα/Cp]/2
Errors and omissions excepted.
Michele
Dear Michele,
ReplyDeleteIf I understand correctly, both the bottom cells start at temperature T, is that correct?
α = mg/p
ε = Rα/Cp
β = Cvα/Cp
I believe we have δh = hδT/T = mRδT/p
In your specific thermal energy of the cells, I think you must divide by 2 to get the average energy per kilogram, so it should be TCv. I assume you are talking about the specific energy before we heat up the lower cell.
In your final specific thermal energy of the cells, I believe you forgot to multiply the δT term by Cv, and you must divide by 2 also, so it should be TCv+δT(1−&epsilon)Cv/2. This is the energy after we have heated the bottom cell and after the exchange of cells has taken place.
Your initial potential energy is the average potential energy of the gas in the two cells before we heat up the bottom cell. But I think this must be divided by 2 also.
Epi = gh(1 + α/4)
The final specific potential energy of the cells is
Epf = g(3h(1+α)(1−β) + (h+δh)(1+β))/4
= g(h + 3αh/4 − βh/2 + δh/4)
So I get for the change in energy:
ΔE = CvδT(1−&epsilon)/2 + g(2hRα/Cp + δhCvα/Cp)/4
This change of energy includes the energy we put in during the heating process, minus the work done by the cells as they change places. The kinetic energy, which becomes viscous heat, is not included in the calculation.
Also, the work done raising the cells above the bottom two is not included in the calculation. Not only do we raise the upper cells when we heat the bottom cell, we raise them again when the two cells exchange places.
So, in my calculations of Buoyancy Work and Expansion Work, I start with the cells before heating, and end with the cells in an identical state after cooling. We find that we remove less energy when the warm cell cools than we put in to heat the cell in the first place. This missing energy is the impetus for convection.
Yours, Kevan
Kevin, you are right relatively to T, α, β, ε, δh.
ReplyDeleteMy last formula was wrong and I rectify it.
ΔE= CvδT(1-ε)+g[2h(α-β)+ δh]/2= CvδT(1-ε)+g(hαR/Cp+ δh/2)
Whit “specific energy” expression I intended the ratio E/M, that’s the energy of the system of two cells. I agree whit you, it isn’t very proper.
My initial conditions are before the heating of the bottom cell.
The correct final specific thermal energy of the two cells should be Ethf=Cv(Tf1+Tf2)=Cv[(T+δT)(1-ε)+T(1+ε)]=2CvT+ CvδT(1-ε).
There was missing a square bracket and the Cv.
For the global energy balance of the two cells we have to take into account
- the total heat that we put in Q = M(CpδT+gδh/2)
- the total external work on all the cell above the second row W = [(hf1+hf2)-(hi1+hi2)]A(p-2mg) = ( δh+δhβ-hαβ)Ap(1-2α) = δhAp(1-2α)
- the total energy gained by the two cells E=MCvδT(1-ε)+Mg(hαR/Cp+ δh/2)
whit the condition Q = E + W
Michele
Dear Michele,
ReplyDeleteI agree with your expression for ΔE. The final term in the expression I wrote down above is wrong.
I claim that you will find there is energy missing when you exchange the cells, and this energy will be equal to gδh/2 per kilogram of gas in the two bottom cells, or Mgδh total in Joule.
Yours, Kevan
The total external work on all the cells above the second row is W = δhAp(1-2α) that is the same which is done during the initial isobaric expansion. That’s the change of place between the first two cells don’t exert anything on all the above cells.
ReplyDeleteThis means that, once the bottom cell is heated, the rising-expansion of the warm cell and the falling-compression of the neighboring cold cell above it, which occur adiabatically and without external work, is an iso-energetic process for the two cells, i.e., Σ(CvT+gz)=const.
Michele
Dear Michele,
ReplyDeleteI think I agree with you: there is no source of work to accelerate the bottom cell so that it takes the place of the cell above it, when we have only a single column of cells.
Buoyancy is caused by two cells being next to one another (at the same altitude) with one less dense than the other. So there is no buoyancy if you consider only one column of cells. There is no reason for the gas to circulate.
If we have a thin column of air, as between two windows placed 1 cm apart, convection does not occur because viscosity does not allow 0.5-cm cells to slide past one another.
Yours, Kevan
In the case of four cells we have that
ReplyDelete- one cell of the first row and one cell of the second row don’t change their energy
- only one cell of the first row is heated, rises to second row and expands adiabatically
- only one cell of the second row come down to the first row and is compressed adiabatically.
In terms of energy is the same think to refer to one column or to two columns.
By the way, I missed the work for the displacement of the cells; then what stays constant is Σ(CpT+gz).
Michele
Dear Michele,
ReplyDeleteI disagree with your first statement. Both cells on the second row change their energy. The only cell that does not change its energy is the one that moves sideways on the bottom row.
The warm cell moves up. It loses internal heat and it loses pressure energy, but it gains gravitational potential energy equal to its loss in pressure energy.
The cell on top of the warm one moves sideways. It does not lose internal energy. It does not lose pressure energy. It loses gravitational potential energy. This is the source of the buoyancy work.
The other cell on the top moves down. It gains internal heat and pressure energy. But its increase in pressure energy is equal to the gravitational potential energy it loses.
The final cell on the bottom moves sideways and is unchanged.
Thus the only place where we have a net loss of energy is the cell that moves sideways on the second row.
Yours, Kevan