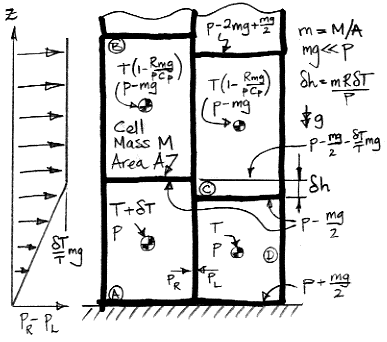
The temperature of cell D is T. Cells B, C, and D have the same enthalpy. If D were to expand adiabatically from p to p−mg, it would cool to the same temperature as B and C. When gas expands adiabatically, TpR/Cp remains constant, where Cp is the heat capacity of the gas at constant pressure and R is the gas constant. When pressure scales by (1−mg/p), temperature scales by (1−mg/p)R/Cp. Because mg≪p, the temperature of the upper cells is very close to T(1−Rmg/pCp).
Cell A has been warmed by a small amount δT compared to cell D. Because it is warmer, it is taller than cell D by δh=mRδT/p. Cell B rises above cell C by a distance δh, and cell A itself rises by δh/2 compared to cell D
In our simulation program, we assume the temperature and pressure within each cell is uniform. Here we allow for variation in pressure from the top to bottom. The top is at p−mg/2 and the bottom is at p+mg/2, so that the total change from top to bottom is mg.
At the top of cell D, the pressure is p−mg/2, but the pressure within A at the same height is greater by mgδT/T. On the left side of our diagram is a graph of the excess pressure in cell A with altitude. Cell A pushes sideways into cell D with an average pressure mgδT/2T. Cell B pushes upon cell C with average pressure mgδT/T, which is twice as much. Cell B starts to push its way over the top of cell C, and in doing so places some of its own weight upon cell D. This additional weight causes the pressure at the base of D increases, and now cell D starts to push its way under cell A, forcing it upwards.
Thus cell A becomes buoyant, and the four cells will rotate clockwise to allow A to rise. Buoyancy manifests itself not only as an upward force upon the buoyant cell, but also as horizontal forces upon the cells above and beside the buoyant cell. The cells above slide out of the way, and the cells beside it push inwards. It is only after these horizontal movements have begun that the buoyant cell can rise.

If we consider the warmed cell and the resultant pressures acting on its sides, ”(see the representation here)” , we obtain
ReplyDelete- two identical vertical forces both pushing upward the bottom side and the top side, i.e., the buoyancy on the entire cell
and
- two identical horizontal forces toward the outside acting on the upper half lateral sides and emptying the cell
- two identical horizontal forces toward the inside acting on the lower half lateral sides and filling the cell.
If the lateral sides of the cell was rigid then the effect of the forces above would be a rotation clockwise of the right side and an anticlockwise rotation of the left side. But this hypothesis is very insubstantial.
Thus I think that the warmed cell rises changing its contents.
Michele
I try again for the link
ReplyDelete”(ITS REPRESENTATION IS HERE)”
Sorry, it doesn't work.
ReplyDeleteMichele
I tray again.
ReplyDelete”(its representation is here)”
Michele
If we consider a string of warmed cells, the resultant pressures and forces acting on their sides,
ReplyDelete”(here)”
we obtain that only the outmost cells experience the horizontal forces R2 (and tend to vanish) while the intermediate cells experience only the vertical forces R1 (the buoyancy) and rise. Obviously the central cells will arrive much higher when the string is larger.
Michele
Dear Michele,
ReplyDeleteThank you for your diagrams. You make a fascinating point about the rotation of the sides of the cells. The rotation will cause the top of the cell to get wider, and the bottom of the cell to get narrower.
When it comes to the string of cells, I am thinking about it. It seems to me that the pressure at the bottom of the cells is equal to the weight of the air above. How could the pressure be higher all along the bottom? How could it be lower all along the top? For the single cell, we see dense air moving into the cell volume from the sides. The light air moves up.
In my example, the pressure at the base of the cells is initially the same. It is only when air starts to move off the top of the warm cell and onto the cold cell that the pressure at the base of the cold cell increases. It seems to me that the rotation of the vertical edges of the cell are what forces it upwards. In the case of your string of cells, the cells at the edge will be forced up first, and once they are out of the way, the inner cells will be forced up in the same way, until they all start moving.
Once the string gets moving upwards, an equilibrium flow will establish itself, and the bubble's velocity will be dictated by viscous friction. At that point, I'm sure the center cells will be ahead of the ones at the edge.
Yours, Kevan
I refer to the stack effect that occurs in a building during the heating season. Due to the buoyancy, the indoor warmer air rises and escapes through open windows at the top and the outdoor colder air enter the open doors/windows at the bottom. The neutral plane in a building is located between the high and low openings at which the internal pressure will be the same as the external pressure. Above the neutral plane, the air relative pressure will be positive and the air pushes outside. Below the neutral plane the air relative pressure will be negative and the external air will push inside.
ReplyDeleteThe cells are entirely opened each other and so I think it is true to suppose that the neutral plane is at half height of the cells.
Michele
Dear Michele,
ReplyDeleteI agree that once the flow starts, the neutral plane will be at the center of the building, and at the center of the cell. Thank you for your description of buoyancy within a building. I suppose the same thing would happen in reverse if it's hot outside and the building is cold from the night.
In the case of the building, we have vertical walls that stop the sides rotating. Air rushes in at the bottom, losing pressure because of its acceleration, so that it is in equilibrium with the lighter air inside.
What if the building were wide and short? I think air would rush in through the doors at the bottom, and out through the windows at the top, but there would be very little movement of air in the center of the building.
Yours, Kevan
If the windows were realized with a very elastic material and they were to perfectly airtight along their perimeter, I think that we would see the high windows to swell themselves outside and the low ones inside. And this without flow, as the pressures are been obtained whit the hydrostatic equilibrium.
ReplyDeleteMichele
Dear Michele,
ReplyDeleteYes, I agree with that. I assume that the top and bottom windows are closed, which is why there is no flow. So we have windows bulging out at the top, and in at the bottom.
If we open the bottom and top windows, air rushes in at the bottom, and drops in pressure, so it is in equilibrium with the air at the bottom-center of the building. This same air rises, but its pressure does not drop as fast as the air outside, so when it reaches the window at the top, it rushes out with acceleration, and once again drops in pressure so that it is in equilibrium with the air outside the top of the building. Thus I claim the air accelerates twice: once on the way in, and once on the way out.
How about simulating this building system with your FreeFem++ program? We could see what happens to the air at the center of a wide, low, building, and how fast the air moves around the edges. I would love to see the results, if you have the time to do it.
Yours, Kevan