Expansion Work

Whenever we allow a block of four cells to rotate within our atmospheric simulation, we see a warm cell rise and expand while a cold cell falls and contracts. The expanding cell is larger, so it does more work than is required to compress the smaller, falling cell. In Impetus for Convection, we called the excess work done by the rising gas expansion work. Our CC5 program assumes the expansion work is equal to CpΔT, where Cp is the specific heat capacity of the gas at constant pressure, and ΔT is the drop in the average temperature of the rotating cells. Today we show that the correct value for expansion work is roughly one third less, and we find that its correct value is exactly equal to the work required to raise up the gas above the rotating block.

When a gas expands adiabatically, it does work pushing outwards, but no heat passes through its boundaries. By the First Law of Thermodynamics, the work done must be equal to the decrease in the internal heat of the gas. The internal heat of a kilogram of ideal gas is CvT, where Cv is its specific heat capacity at constant volume. A kilogram of gas that has cooled by ΔT through adiabatic expansion must have done CvΔT of work as it expanded. For air, Cv = 716 J/kgK, so this work would be 716 J/kg for a cooling of 1°C. If we multiply ΔT by Cp instead of Cv, we get a value 1003 J/kg, which is 313 J/kg too high.

Let us return to the four cells we considered in Buoyancy Work, and calculate the expansion work in terms of the same parameters. As before, we start with a block of four cells that has no tendency to circulate, and we warm the lower-left cell by δT. We use R for the specific gas constant. As always, we have Cp=R+Cv.



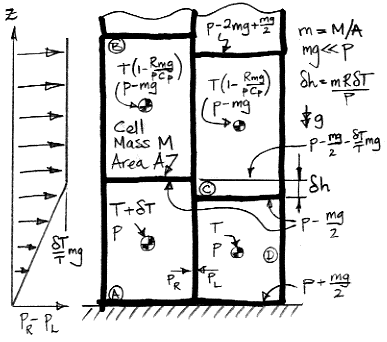
Before rotation, cell A is at T+δT. When it rises, it expands adiabatically from pressure p to p−mg. When mg≪p, the temperature drops by a factor of 1−Rmg/pCp. When cell B falls, it temperature begins at T(1−Rmg/pCp) and ends at T. A few lines of calculations will reveal that the drop in the average temperature of the four cells is simply δTRmg/4pCp. The expansion work, We, per kilogram of gas is:

We = δTRmgCv/4pCp

We have seen this quantity before. In Buoyancy Work we found that the work required to raise the gas above the block was δTRmgCv/4pCp. In our next post, we will explore the implications of this equality, and at last solve the mystery we presented in Impetus for Circulation.